[알고리즘] Dynamic Programming

HM·2023년 7월 21일

알고리즘 스터디

목록 보기

1/1

하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장, 다시 큰 문제를 해결할 때 저장된 결과를 사용하는 방법. 즉, 답을 재활용한다고 생각하면된다.
메모리를 적절히 사용해 수행 시간 효율성을 비약적으로 향상 시키는 방법이다.
대표적인 DP 문제 : ⭐️배낭문제⭐️, 1로 만들기, 화폐 구성, 피보나치 수열 등

DP 사용 조건

최적 부분 구조 (Optimal Substructure)
: 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 경우.
중복되는 부분 문제 (Overlapping Subproblem)
: 동일한 작은 문제가 반복적으로 발생하는 경우.

DP 문제 접근법

주어진 문제가 DP 유형임을 파악하는 것이 중요.
그리디, 구현, 완전 탐색 등의 아이디어로 해결할 수 있는지 검토해보고, 다른 알고리즘 풀이가 떠오르지 않으면 DP를 고려해볼 것.
먼저, 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한다. 작은 문제에서 구한 답이 큰 문제에서 그대로 사용할 수 있으면 코드를 개선함. (탑다운)
일반적인 코테에서는 기본 유형의 DP 출제

DP 풀이방식

DP 문제에서 제일 유명한 피보나치 수열을 예시로 들었다.

피보나치 수열 이란?

피보나치 수열은 아래 예시와 같이 첫 번째 항과 두 번째 항이 1이며 그 뒤의 항은 바로 앞 두 항의 합인 수열이다. 편의상 0을 0번째 항으로 놓기도한다. 이 수열을 이루는 숫자를 피보나치 수라고 부른다.

(0), 1, 1, 2, 3, 5, 8, 13, 21, 34, .....

피보나치 수열을 재귀적으로 구하는 함수는 아래와 같다.

public int fibo (int n) {
    if (n < 1)
        return 0;
    // 첫 번째 항이거나 두 번째 항이면 무조건 1이기 때문에 1을 반환해준다.
    if (n == 1 || n == 2)
        return 1;
    return fibo(n - 1) + fibo(n - 2);
}

문제는 이 메소드를 호출하게 될 경우 아래 그림처럼 매우 많은 횟수의 호출과 중복이 일어나게 된다.

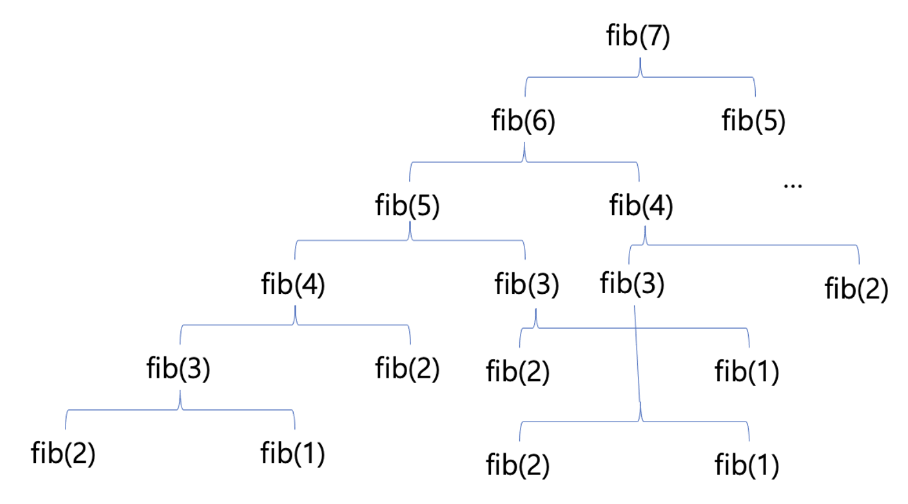
이런 경우 재귀적으로 문제를 풀 필요없이 값을 더해 나가며 앞의 부분 문제의 결과를 다음 문제의 답을 구하는데 활용이 가능하다. 즉, DP를 이용해 편리하게 구할 수 있는 것이다.

탑 다운 (하향식) : 큰 문제를 해결하기 위해 작은 문제를 재귀적으로 호출, 작은 문제들이 해결됐을때 큰 문제에 대한 답을 얻을 수 있도록 구현하는 방식.

메모이제이션 (Memoization) ➡️ 탑다운 방식에서 사용
- 한 번 계산한 결과를 일시적으로 메모리 공간에 저장해놓는 기법.
  DP에 국한된 개념은 ❌
- 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져옴.
- 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 함.

import java.util.*;

public class Main{
    // 탑다운 방식 중 메모이제이션 피보나치 수열 코드 예시
    public static long[] d = new long[100];
    public static void fibo(x){
        System.out.println("f("+x+")"+" ");
        if(x==1 || x==2)
            return 1;
        if(d[x] != 0)
            return d[x];
        d[x] = fibo(x-1) + fibo(x-2);
        return d[x];
    }
    public static void main(String[] args){
        // 첫 번째 피보나치 수, 두 번째 피보나치 수 = 1
        d[1] = 1;
        d[2] = 1;
        int n = 50; // 50번째 피보나치 수 계산
        System.out.println(fibo(n));
}

바텀 업 (상향식) : 아래쪽부터 작은 문제를 해결, 먼저 계산된 문제들의 값을 활용해 그 다음의 문제까지 차례로 해결하는 방식. 반복문 활용
DP의 전형적인 형태 = 바텀 업 방식
결과 저장용 배열 or 리스트 = DP 테이블 이라고 부른다.

import java.util.*;

public class Main{
	// 바텀 업 방식 피보나치 수열 구현 예시
    public static long[] d = new long[100];
    public static void main(String[] args){
        // 첫 번째 피보나치 수, 두 번째 피보나치 수 = 1
        d[1] = 1;
        d[2] = 1;
        int n = 50; // 50번째 피보나치 수 계산

        //피보나치 함수 반복문으로 구현(보텀업 DP)
        for(int i=3;i<=n;i++){
            d[i] = d[i-1] + d[i-2];
        }
        System.out.println(d[n]);
}

DP vs 분할정복

동적 계획법과 분할 정복의 경우 큰 문제를 작은 부분 문제로 나누어서 풀어낸다는 점에서 유사한 모습을 보이지만, 차이점도 존재한다.

공통점 : 두 방법 모두 최적 부분 구조를 가질 때 사용가능
➡️ 큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황
차이점 : 부분 문제의 중복
- DP 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복되는 반면, 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않음.
  ➡️ 즉, DP는 각 부분 문제가 어느정도 서로에게 의존성을 가지고 있지만, 분할 정복은 개별 문제가 독립적으로 풀어낼 수 있으며 병렬적으로 처리가 가능하다.

나만의 공부방 📖

[알고리즘] Dynamic Programming