(고수B) 4. 평균값 정리와 테일러공식

본 포스트는 작성자가 중국 북경대학교에서 22-23학년도 1학기 고등수학B(1) 수업을 들으며 배운 내용을 복습하며 정리한 포스트입니다. 중국어, 한국어, 영어가 뒤섞인 본인이 알아보기 위해 작성한 필기를 정리하는만큼 다른분들이 읽기엔 조금 불친절할수 있습니다.

중간고사가 끝나고 시작되는 챕터다. 다들 중간고사는 잘 보셨나요...?

4.1. 중간값 정리

롤의 정리

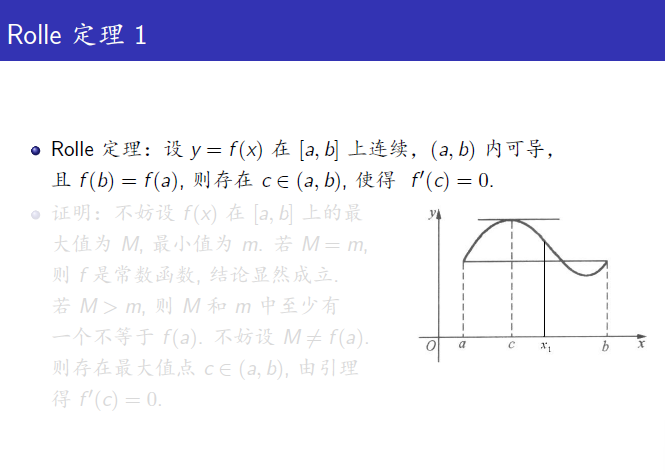
롤의 정리: $y=f(x)$가 $[a,b]$의 구간에서 연속하고 $f(a)=f(b)$라면 위의 구간에 속하는 $c$가 있고, $f'(c)=0$이 된다.

롤의 정리로 $f'(c)=0$을 만족하는 점 c가 (a,b)에 있다는건 증명할 수 있지만, 특정한 위치와 위를 만족하는 점이 몇 개가 있는지는 알아낼 수 없다.

라그랑주 중간값 정리

(라그랑주) 중간값 정리:$y=f(x)$가 $[a,b]$의 구간에서 연속하고 $(a, b)$구간에서 미분 가능하면, 위 구간 에 $f'(c)=\frac{f(b)-f(a)}{b-a}$가 성립되는 점 $c$가 존재한다.

$f'(c)=\frac{f(b)-f(a)}{b-a}$는 사실 점 $(a, f(a))$와 $(b, f(b))$사이를 잇는 선의 기울기인데, $f'(c)$가 마침 $(c, f(c))$에서의 기울기값이고, 이는 저 선과 평행하기에 이런 결과가 나온다.

중간값 정리식은 $f(x)=f(x_0)+f'(c)(x-x_0)$으로도 표현된다.

함수의 미분과 단조성

꽤나 직관적인데, 미분값에 따라 $f(x)$의 $[a,b]$구간 상의 증감성을 알 수 있다.

이에 따른 예시다. $f(x)$의 단조구간을 구하는데, 우선 미분 한 후 $x$가 0이나 2일때 미분값이 음수기 때문에 (0,2)에서 严格单调下降하고, 나머지 구간에선 양수기에 严格单调增함을 알 수 있다.

응용 증명

첫 예시는 간단하고, 두번째 예시의 경우 우선 반증법으로 근이 3개있다고 가정하고, 롤의 정리를 이용해 미분값이 0이 나올수 없음을 증명하여 모순을 보인다.

롤 정리에 의해 함수 $f(a)=f(b)=0$이라면 (a,b)구간에 속하는 값 c가 있고 $f'(c)=0$이 될 것임으로 $f'$도 이 구간에 근이 있음을 알 수 있다.

교과서 시티 6번이다. 주어진 $f(x)$의 근이 있음을 구해야 하는데, 적분해서 $g(x)$를 구하고 이 함수가 롤 정리를 구간에서 만족함을 증명하면, $f(x)$도 이 구간에 근이 있음을 위 원리를 이용해 알아내는 방식이다.

4.2. 코시 중간값 정리, 로피탈 법칙

코시 중간값 정리

로피탈의 법칙

고등학교때도 배운 로피탈의 법칙이다.

4.3. 테일러 공식

고등학교때도 배웠던 테일러 공식의 기본 정의다.

위의 공식을 제대로 외우고 있는것이 중요하다.

테일러 공식으로 극한을 찾는 예시다.

4.4. 테일러 공식의 余项

위의 테일러 공식중 $o$항은 뒤의 더 높은 차수의 无穷小量을 뜻하나, 정확히 얼마나 큰지는 알 수가 없다. 이를 위해서 고안된게 라그랑주 중간값 정리를 활용한 테일러 정리다.

마지막 항 하나로 $n+1$번째 부터의 모든 항을 표현할 수 있다. 주의할점은 마지막 항은 $f^{(n+1)}(x_0)$이 아니다.

나머지항이 포함된 테일러 공식이다.