본 포스트는 작성자가 중국 북경대학교에서 22-23학년도 2학기 고등수학B(2) 수업을 들으며 배운 내용을 복습하며 정리한 포스트입니다. 중국어, 한국어, 영어가 뒤섞인 본인이 알아보기 위해 작성한 필기를 정리하는만큼 다른분들이 읽기엔 조금 불친절할수 있습니다.

마지막 장이다!

12.1 삼각함수계와 정교성

개념만 짚고 넘어간다.

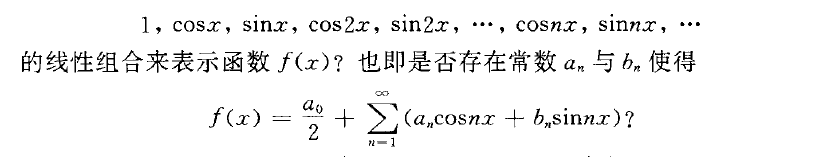
위와 같은 형식의 주기가 2파이인 삼각함수로 이루어진 급수를 삼각급수라고 한다. 주기가 2파이인 경우 기본삼각함수계라고 한다.

기본삼각함수계의 어떤 2개의 함수를 서로 -파이부터 파이까지 적분하면 항상 0이 된다는 사실을 알 수 있다. 이 성질을 해당 구간에서 정교하다 라고 한다.

-파이부터 파이까지의 모든 유계 적분 가능한 함수의 모음을 집합공간으로 보고, 그 안의 모든 함수를 벡터라고 보자. 여기에서 벡터 2개 f와 g를 두고 (f,g)는 위처럼 内积라고 하고, 아래를 벡터 f의 范数라고 한다.

12.2 주기가 2파이인 함수의 푸리에 급수와 수렴성

푸리에 급수

f(x)가 주기가 2파이인 함수라고 하고, -파이부터 파이까지 유계 적분 가능하다면, 우리는 위의 a_n과 b_n을 푸리에계수라 부르고, 밑의 식을 푸리에 급수라고 부른다.

푸리에 급수의 수렴성

f(x)가 [a,b]에서 1형 间断点을 없애면 处处连续할때 分段连续，[a,b]에서 유한한 단조구간만이 있으면 分段单调하다고 한다.

디리클레 정리다. 위 정리는 즉 分段连续하며 分段单调한 함수는 연속한 점에서는 푸리에 급수가 해당 점의 함수값에 수렴한다는 뜻이며, 이때 우리는 함수가 이 점에서 푸리에 급수로 전개 가능하다고 말한다. 하지만 间断点에서는 해당 점의 좌우 극한의 평균값에서 수렴한다.

寄偶주기함수의 푸리에 급수

偶函数인 경우 bn이 0이 되고, 반대의 경우는 an이 0이 된다.

任意周期함수의 푸리에급수

2파이 외의 주기에서는 위의 식을 활용하면 된다. l=주어진 주기/2다.