
차원의 저주
많은 설명변수(feature, X)가 존재할 때 전체 데이터의 양이 너무 많은 경우,
- 전체 데이터의 양이 너무 많아서 학습 속도가 느려질 수 있다.
- overfitting될 우려가 있다.
Solutions
1. Manifold Learning
2. PCA
Manifold Learning
Assumptions
A. Manifold Hypothesis
= 고차원 데이터라 할지라도, 실질적으로 해당 데이터를 나타내주는 저차원 공간인 manifold(위상 공간)가 존재한다.
= 처리해야 할 작업이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것이다.
B. Locally Linear Embedding(LLE)
= 무엇보다 중요한 것은 샘플간 선형 관계이다.
1. 모든 훈련 샘플에 대해 각각 가장 가까운 k개의 샘플을 찾는다.
2. 각 샘플이 이웃에 대한 선형관계로 표현되는 오차를 최소화한다.
3. 선형 관계를 보존하면서 하위 부분 공간으로 매핑한다.
C. t-distributed stochastic neighbor embedding
= 가까이 있는 것은 더 가까이, 멀리 있는 것은 더 멀리 하면 분류하기 쉬울 것이다.
D. multi-dimensional scaling (MDS)
= 샘플 간 거리를 보존하는 것이 무엇보다 중요하다.
PCA
PCA
= 주성분 분석(principal component analysis)
= 데이터에 가장 가까운 초평면을 정의하여 데이터를 투영시키는 차원 축소 알고리즘
= 공간에 표현된 데이터의 정보 손실은 줄이면서 차원축소하는 방법.
= 분산을 최대로 보존하여 정보의 손실을 가장 적게 유지하자.(원본 데이터셋과 투영된 것 사이의 평균제곱거리를 최소화하자)
- 공분산 : 한 변수간의 변동을 분산, 두 변수 간의 변동은 공분산
- 고유 벡터: (화살표) 행렬X에 다른 행렬A를 곱했을때, 행렬X의 벡터들 중 벡터의 크기는 변하지만, 방향은 변하지 않는 벡터
- 고유값 : 해당 고유 벡터의 크기 (화살표의 길이)
- 선형변환 행렬X 에 다른 행렬A 를 곱해줌으로써 공간 A에 행렬X 를 맵핑(mapping, 투영/사상이라고도함) 시켜주는 개념.
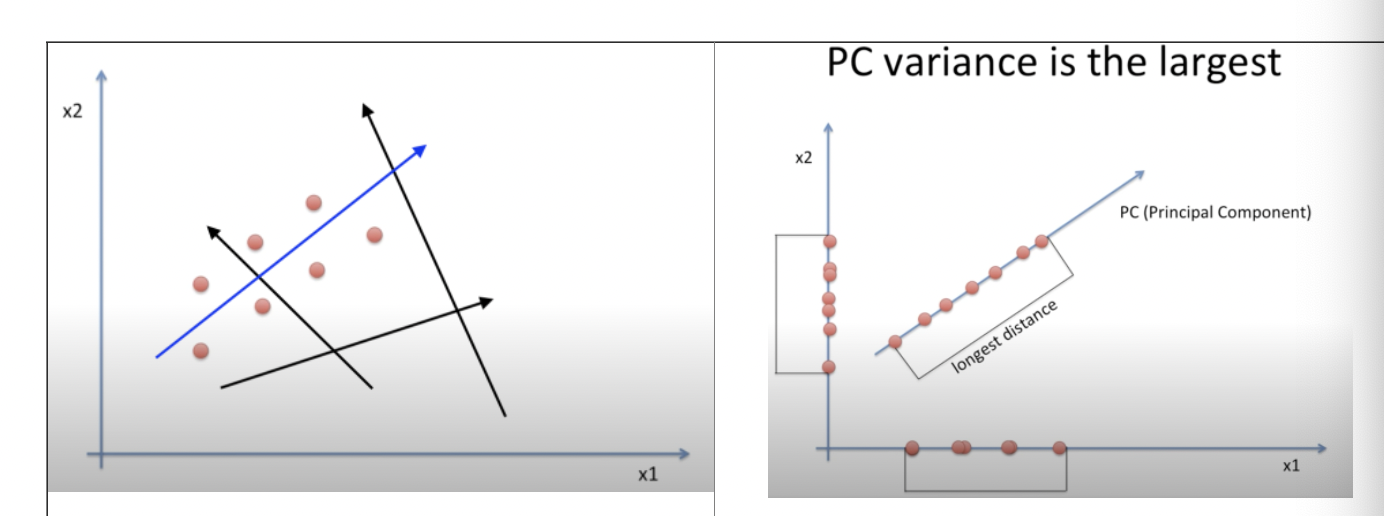
그래프에서 파란색 화살표라는 새로운 직선에 데이터를 투영했을 때, 데이터가 겹쳐서 투영되면 정보 손실이 있는 것이다. 따라서 데이터가 최대한 안 겹치고 멀리 퍼지게 하는 길이가 긴 화살표를 찾는 것이 PCA의 목적이다.
→ 데이터가 최대한 안겹치고 : 분산이 가장 크다(공분산 행렬에서)
→ 화살표 찾자 : 공분산 행렬에서 고유벡터, 고유값 찾자.(항상 음이 아닌 고유값을 갖는다.)
공분산행렬 : 변수들에 대해 대각성분에는 자기 자신의 분산을, 나머지 성분은 서로 다른 두 변수간의 공분산을 적은 행렬
- 공분산 행렬은 대칭행렬일 수 밖에 없다.
- 각 데이터 특징들의 변동이 서로 얼마나 닮았는지 확인할 수 있다.
공분산 행렬 구하기
SVD 특이값 분해
SVD(Singular Value Decomposition) = 행렬을 분해하는 것, PCA의 결과가 된다.
대각화(diagonalization) : full rank일 때만 가능(rank = 행렬에서 일차 독립인 열의 개수)
- 대칭행렬에서는 고유벡터를 직교 행렬로, 고유값을 정방행렬로 대각화할 수 있다.
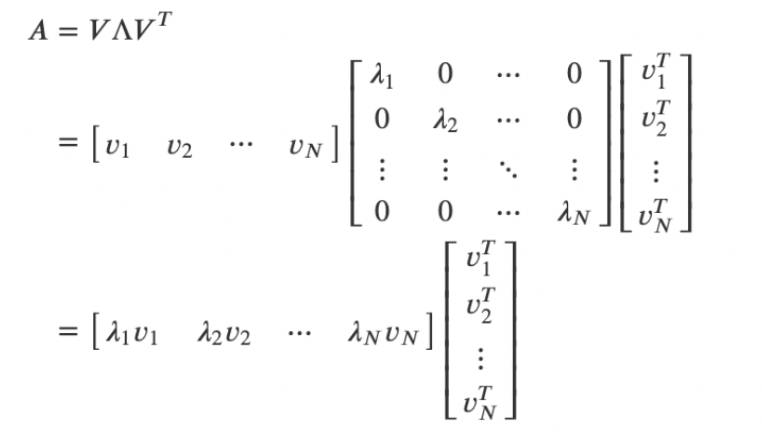
그럼 위의 그림에 의해 공분산 행렬에서 eigenvalue 구하면 가운데 대각화한 행렬에서 고유값 행렬임
맨앞의 가로 행렬 = 가장 분산이 큰 방향을 가진 고유 벡터
맨뒤의 세로 행렬 = 그 다음으로 가장 분산이 큰 방향을 가진 고유 벡터
대각행렬 = 고유값 = 화살표의 길이
고유 벡터들이 가장 분산이 큰 화살표이다. 고유값 가장 큰(화살표의 길이가 가장 긴) k개의 고유벡터 추출하여 고유값이 가장 큰 순으로 정렬된 고유벡터를 이용해 입력 데이터들을 선형 변환한다.
고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력데이터들을 선형변환(고유벡터^T 와 원데이터^T 내적 후 분산 구함)한다.
고유값 전체의 합 = 원데이터의 분산
PCA(직접) 구현하기
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# i) generating (1000 samples X 100 features) random data matrix
#generating (1000 samples X 100 features) random data matrix
np.random.seed(42)
X = np.random.rand(1000,100)
#Check X
X
# ii) performing the PCA on it
def PCA(X):
#find the covariance of data consisting of 100 features and 1000 observations.
X_mean = X.mean(axis=0)
X_centered = X - X_mean #Calculate the deviation.
#Dot product
#Since we find the covariance for the data consisting of 1000 observations, we divided it by 999.
X_covariance = np.dot(X_centered.T, X_centered) / 999
#Calculating eigenvalue and eigenvector
eigenvalue, eigenvector = np.linalg.eig(X_covariance)
#arrange eigenvectors in order of eigenvalue size
index = np.argsort(eigenvalue)[::-1]
eigenvector = eigenvector[:, index]
#eigenvector selection
pca_result = np.dot(eigenvector.T, X_centered.T).T
pca_y = np.var(pca_result, 0)
return pca_y
PCA(X)
# iii) drawing a chart (X-axis = principal components in decreasing order of eigenvalues, Y-axis = variance)
x = list(range(100))
y = PCA(X)
#drawing a chart (X-axis = principal components in decreasing order of eigenvalues, Y-axis = variance)
from matplotlib import pyplot as plt
plt.plot(x,y)
plt.xlabel('principal components in decreasing order of eigenvalues')
plt.ylabel('variance')
plt.show()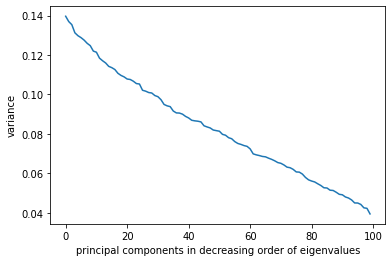
PC 수 선택 방법
A. eigenvalue가 1이상일 때까지
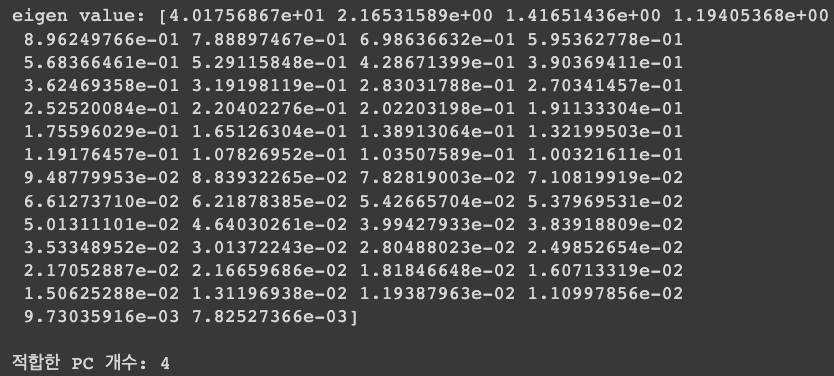
- 적합한 PC 개수 : 4
B. Scree Plot 그래프 기울기가 완만해지기 전까지
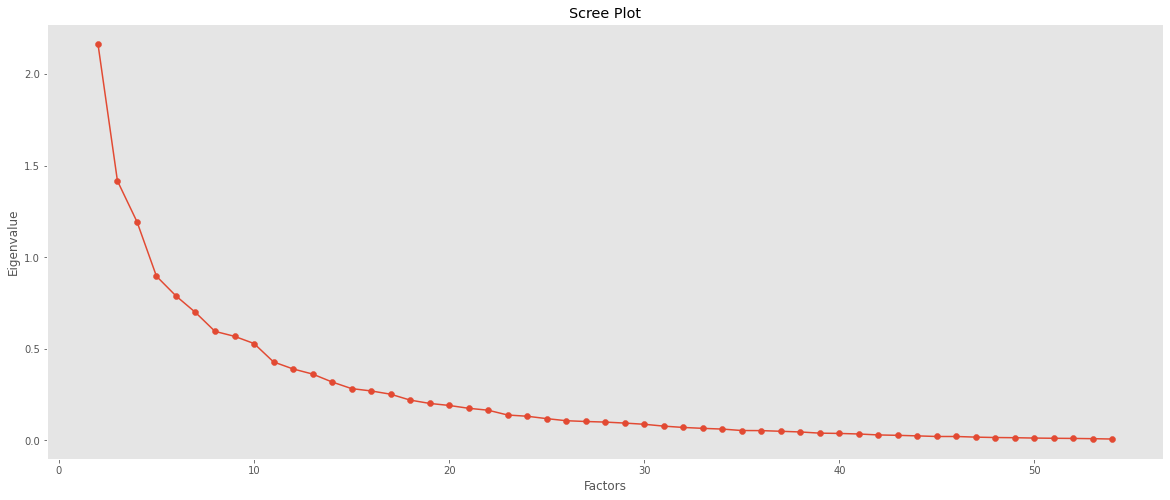
- 적합한 PC 개수 : 4(확대하여 그려보면 알 수 있음)
*Scree Plot의 경우 특정 수치가 아닌 주관적인 해석일 수 있으므로 주의해야 한다.
C. 80% 이상의 분산을 설명할 때까지
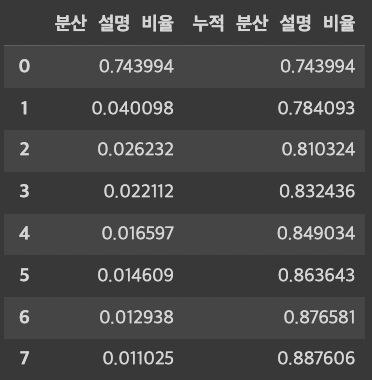
- 적합한 PC 개수 : 2