Learning Method

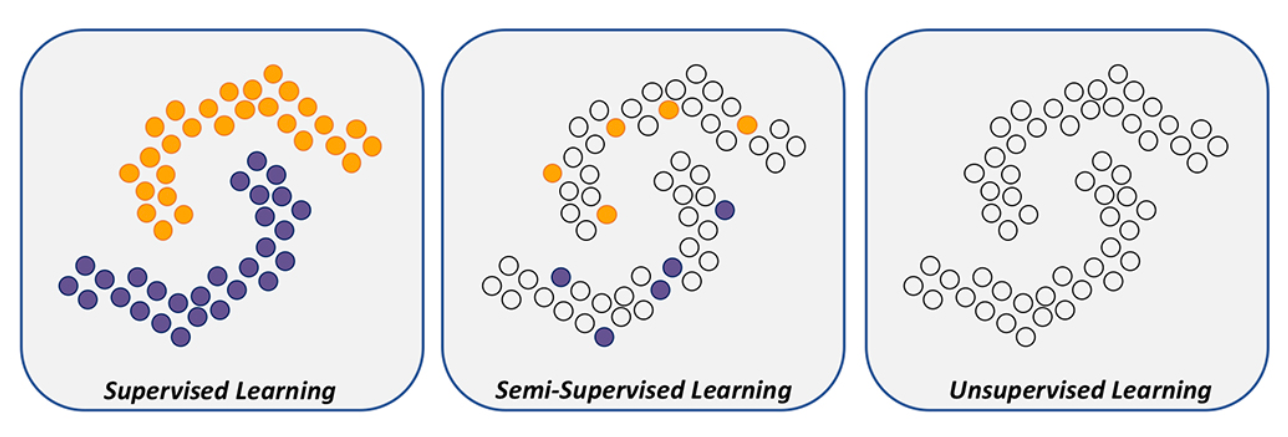
supervised 는 모든 데이터들이 label을 가지고 있음
semi-sipervised는 극히 일부의 데이터들만 label을 가지고 있음
unsupervised는 데이터들이 label이 아예 없을 때.
(clustering도 이 unsupervised이고 clustering을 먼저 진행하고 fine tuning을 통해 class를 정하는 방식으로 이루어진다)

만약 두번째 semi-supervised 상황에서,
label 있는 것만 가지고 학습을 하게 되면 decision boundary가 overfitting이 될 수 있다.
이것을 막고자 unlabel 데이터를 잘 활용하자는 접근 방법이 바로 semi-supervised learning이다.

Semi-supervised learning

Learning Objective

Learning Objective 함수는 Main Objective $\mathcal{L}_\tau\left(\theta, D_\tau^L\right)$와 Auxiliary Objective $\lambda \cdot \mathcal{L}_{\text {aux }}\left(\theta, D_\tau^L \cup D_\tau^U\right)$ 두 가지의 함수로 나타낼 수 있다.

Main Objective: task-oriented objective

$\mathcal{L}_\tau\left(\theta, D_\tau^L\right)$

• supervised learning with ERM
• use only labeled data

Auxiliary Objective: regularization

$\lambda \cdot \mathcal{L}_{\text {aux }}\left(\theta, D_\tau^L \cup D_\tau^U\right)$
메인은 이것! 이것에 따라 generalization 성능이 결정된다.

• improve generalization / task performance
• mainly use unlabeled (and also labeled) data

Auxiliary Objective 는 1. Consistency Regularization 방법과 2. Entropy Minimization 방법으로 나뉠 수 있다.

1. Consistency Regularization
model output remains unchanged when input is perturbed
smoothness (비슷한 input 넣으면 비슷한 output 나오도록)

2. Entropy Minimization
prediction 관점에서, 예측 확률의 entropy를 낮추도록
특정 class에서 confident 하게 만들자는 것 (클래스가 분리가 잘 되도록)
(+ uniform distribution은 entropy가 높은 것, 한클래스에서 확률이 더 높으면 entropy가 낮은 것)
self-training / pseudo-labeling

방법1. Pseudo Labeling [Lee, 2013]

Pseudo Labeling은 매우 간단한 방법으로 entropy minimization의 카테고리에 속하는 방식이다.
최대 확률을 가진 클래스를 실제 클래스라고 임의대로 가정해버린다.
라벨이 업는 데이터는 이런 pseudo-label을 이용해 학습하게 된다.
entropy minimization이랑도 동일한 컨셉이고, 예측 값을 high-confident하게 만든다.
확률이 높다고 무조건 entropy minimization을 하지는 않고, 특정 threshold를 주고서 하는게 실제로 성능이 더 높게 나온다.

방법2. Π-Model [Laine and Aila, 2017]

위의 Pseudo Labeling에서는 entropy minimization의 카테고리에 속하는 방식이었다면
Π-Model은 Consistency Regularization의 카테고리에 속하는 대표적인 방식이라고 할 수 있다.

같은 input $x_i$를 넣어서 서로 살짝 다르게 augmentation 해줘서 나온 두가지 버전의 output이 $z_i$랑 $\tilde{z_i}$라고 할 때, 두개의 값은 consistency 가정에 의해 비슷한 output이 나오게 된다.
(여기서 특이한 점은 1. 다른 augmentation 사용, 2.NN에 넣어줄 때 drop out도 다르게 넣어줌 )
이 두개의 output의 difference를 구해서 이 차이를 minimization 하는 방식으로 학습한다.

만약 $x_i$에 대한 label $y_i$가 있다고 하면 cross entropy를 이용해 supervised learning 방식으로 학습한다.

여기서 cross-entropy가 Main Objective $\mathcal{L}_\tau\left(\theta, D_\tau^L\right)$ 라고 할 수 있고 squared difference가 consistency를 regularization 하는 Auxiliary Objective
$\lambda \cdot \mathcal{L}_{\text {aux }}\left(\theta, D_\tau^L \cup D_\tau^U\right)$ 라고 할 수 있다.

psuedo code

psuedo code를 살펴보면,
데이터 미니 배치 불러오고 , 서로 다른 형태로 augmenation 하고, drop out도 다르게 함.
레이블이 있는 애들은 cross entropy로 계산, 모든 데이터에 대해서는 augmented 된 결과값의 prediction이 같도록 minimization을 해줌

방법3. Temporal Ensembling

Π-Model 에서 좀더 개선을 해 볼 수 있는게 없을 까 해서 나온 모델이 Temporal Ensembling 이다.
앞의 Π-Model이랑 거의 똑같은데 zi가 모델에서 나온게 아니라 따로 나온다.

이 컨셉을 이해하기 위해 먼저 앙상블의 개념에 대해 알아야 하는데, 만약 Neural Network 같은 아키텍처를 쓴다고 할때, 모델의 파라미터 $\theta$를 바꿔주면서 Prediction을 여러개를 만들어 주는것이 앙상블의 기본적인 컨셉이고, 여러 파라미터에 대해 나온 값을 average하면 더 좋은 prediction을 얻을 수 있다.

이때 파라미터 $\theta_1,\theta_2,\theta_3,...,\theta_t$ 인데 prediction된 값 $z_1,z_2,z_3,...,z_t$을 저장해서 이용하자는 것이 temporal ensemble의 컨셉이다.

$\tilde{z_i}$ 는 t-1까지 누적햇던 예측 값들의 기록, 그 기록에다가 현재의 기록 $z_i$를 얹혀주면 temporal ensemble 효과가 나타난다.

(+ filtering 방법에서 배운 moving average filtering 이랑 비슷한 개념인것 같다. 이전의 정보를 얼마나 반영해서 현재 값을 결정하는지에 대한 개념이다.)

모델 파라미터로써 하는게 아니라 z 자체를 따로따로 관리하는 형태로 접근

result

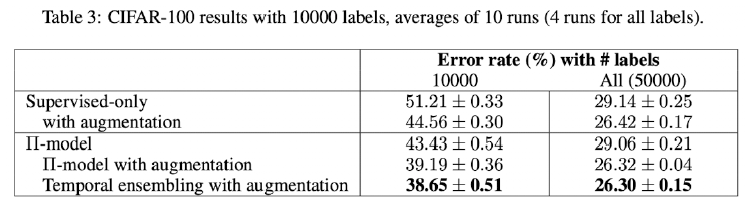
temporal ensemble을 쓰면 성능이 더 높아지긴 했다.

pseudo code

sample N개, N개에 대한 z값을 다 저장을 해줘야 함
그러나 여기서 모든 N개에 대해서 다 기록을 해줘야한다는 것이 정말로 scalable한가? 생각해보아야 한다.
만약 데이터를 1억개를 쓴다면 1억개 데이터에 대한 값들을 다 기록해야하기 때문에 효율적으로 보이지는 않는다.
=> 이것을 개선한 방법이 다음장에서 소개할 Mean Teacher 방법이다.

---

Semi-supervised learning 참고
https://blog.est.ai/2020/11/ssl/
https://jiwunghyun.medium.com/semi-supervised-learning-%EC%A0%95%EB%A6%AC-a7ed58a8f023