📚 셸 정렬(Shell Sort)
단순 삽입 정렬의 장점은 살리고 단점은 보완하여 더 빠르게 정렬하는 알고리즘
💻 단순 삽입 정렬의 특징
- 장점 : 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서 속도가 빠르다.
- 단점 : 삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아진다.
삽입 정렬은 어느 정도 정렬되어 있는 배열의 정렬에는 굉장히 효율적이다. 😁
그러나 삽입 정렬 시 삽입되어야 할 위치가 현재 위치에서 멀리 떨어진 곳이라면 이동 횟수가 증가한다.
삽입 정렬은 이웃 위치로만 이동할 수 있기 때문이다. 😢
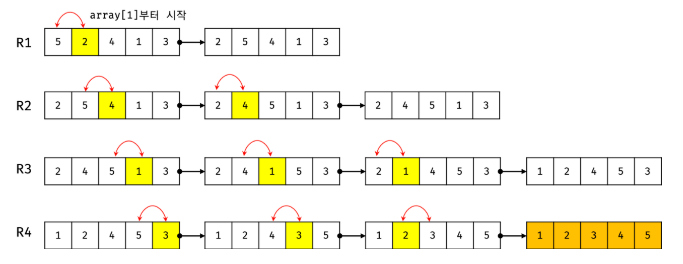
셸 정렬 방법
정렬할 배열의 원소를 그룹으로 나어 각 그룹별로 정렬을 수행한 후, 정렬된 그룹을 합치는 작업을 반복하는 정렬 방법이다.
구체적으로 정렬 방법에 대해 알아보자!
1) 정렬할 배열에서 k 칸 떨어진 원소끼리 그룹을 만들어 그룹 내에서 정렬을 진행한다.
이때, k는 간격(Gap)이라 하고, 간격의 초기값은 (배열 원소의 수)/2가 된다.
2) 한 번의 그룹별 정렬 작업이 끝나면 간격 k를 반으로 줄인다.
이때, 간격은 홀수인 것이 좋기 때문에 k의 절반이 짝수일 경우 +1을 해서 홀수로 만든다.
3) k가 1이 될 때까지 반복한다.
이 방법은 그룹별 정렬이 끝날 때마다 조금씩 정렬된다.
셸 정렬 알고리즘 특징
- 정렬 횟수는 증가하지만 원소의 이동 횟수가 줄어들어 더 효율적인 정렬이 가능하다.
- 연속적이지 않은 배열의 원소 교환이 발생하면 일반 삽입 정렬보다 더 먼 거리를 이동할 수 있다.
- 알고리즘이 간단하다.
시간복잡도
최선의 경우(이미 정렬이 완료된 배열) 각 값을 한번씩만 비교하고, 원소의 교환이 없기 때문에 시간복잡도는 O(n)이다.
최악의 경우(역순으로 정렬된 배열) 각 값을 모두 비교하고, 원소도 모두 교환해야 하기 때문에 시간복잡도는 O(n^2)이다.
삽입 정렬의 경우 최선의 경우 O(n), 최악의 경우 O(n^2)로 유의미한 차이가 아니라고 생각할 수 있지만!
평균적으로 삽입 정렬은 O(n^2)의 시간복잡도를 갖지만, 셸 정렬은 O(n^1.3~1.5)의 시간복잡도를 갖기 때문에 셸 정렬이 평균적으로 더 좋은 성능을 가진다고 생각하면 됩니다!
공간복잡도는 O(n) 입니다~
📚 퀵 정렬(Quick Sort)
퀵 정렬은 가장 빠른 정렬 알고리즘으로 알려져 있으며 널리 사용된다.
분할 정복(divide and conquer) 방법을 통해 주어진 배열을 정렬한다.
💻 분할 정복
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
퀵 정렬 방법
1) 배열 중 하나의 원소를 선택한다.
이 원소는 피벗(pivot)으로, 그룹을 나누는 기준 역할을 한다.
2) 피벗을 기준으로 그룹이 나누어진다. 그룹을 나누는 것을 분할(divide)라고 한다.
피벗보다 작은 원소들은 모두 피벗의 앞으로 이동하고, 피벗보다 큰 원소들은 피벗의 뒤로 이동하도록 하여 배열을 두 그룹으로 분할한다. 분할을 마친 뒤에 피벗은 더이상 움직이지 않는다.
3) 분할된 두 개의 작은 배열에 대해 재귀적으로 이 과정을 반복한다.
퀵 정렬 알고리즘
퀵 정렬은 분할(Divide)과 정복(Conquer) 단계로 구성된다.
-
분할 (Divide)
배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗 왼쪽: 피벗보다 작은 원소, 피벗 오른쪽: 피벗보다 큰 원소)로 분할한다. -
정복 (Conquer)
부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
시간복잡도
평균적인 시간복잡도
- 먼저 각 단계에서 원소 개수인 n 만큼 비교 작업이 수행된다.
- 각 단계의 수는 순환 호출의 횟수라고 생각하면 된다!
만약 8개의 원소를 분할하여 비교하는 작업을 진행한다고 생각하면 처음에는 1개의 원배열, 다음으로 2개의 부분 배열, 그 다음에는 4개의 부분 배열에서 비교 작업을 수행하면 마지막 8개의 부분 배열은 정렬된 결과가 되기 때문에 순환 호출은 3번 발생한다.
따라서 평균적인 시간복잡도는 단계의 비교 횟수인 n과 각 단계의 수 k인 log₂n의 곱으로 O(n log ₂ n)이 된다.
최악 시간복잡도
만약 이미 정렬된 배열 또는 역순으로 정렬된 배열의 경우 단계별 비교 횟수는 n번이고, 순환 호출이 반복될 때마다 1개의 원소가 떨어져 나오기 때문에 n번의 순환 호출이 발생한다.
따라서 최악의 시간복잡도는 O(n^2)이 된다.
📚 병합 정렬(Merge Sort)
배열을 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘
파이썬이 제공하는 heapq 모듈의 merge(a,b) 함수를 사용하면 빠른 병합 정렬이 가능하다!
병합 정렬 방법
정렬을 마친 배열의 병합을 응용하여 분할 정복법에 따라 정렬하는 알고리즘 방법이다!
1) 배열을 앞부분과 뒷부분으로 분할한다.
2) 배열의 앞부분을 병합 정렬로 정렬한다.
3) 배열의 뒷부분을 병합 정렬로 정렬한다.
4) 배열의 앞부분과 뒷부분을 병합한다.
자바의 LinkedList 정렬에 유용하다고 한다!
(퀵 정렬은 오버헤드 발생 증가!)
퀵 정렬과 병합 정렬의 차이점
- 퀵 정렬과 병합 정렬은 분할 정복 알고리즘을 사용하고, 속도가 빠른 정렬 방법이다.
- 퀵 정렬은 불안정 정렬, 병합 정렬은 안정 정렬이다.
- 퀵 정렬은 최악의 경우 O(n^2)의 시간복잡도를 가지지만, 병합 정렬은 항상 O(n log n)으로 동일하다.
- 두 정렬의 공간복잡도는 O(n)이지만 병합 정렬은 임시 메모리 공간이 필요하다.
시간복잡도
- 배열을 병합하는
merge()과정의 시간복잡도는 O(n) 이다.
배열의 모든 원소를 한번씩 비교하여 병합하기 때문이다! - 배열의 분리 횟수는 log ₂ n 번이므로 시간복잡도는 O(log ₂ n)이다.
따라서 병합 정렬 알고리즘의 시간복잡도는 O(n log ₂ n)이다.
📚 힙 정렬(Heap Sort)
힙의 특성을 이용하여 정렬하는 알고리즘
-
최대 힙(Max Heap) : 최대 트리는 각 노드의 키 값이 자식 노드의 키 값보다 작지 않은(=크거나 같은) 완전이진트리
= 부모 노드가 항상 자식 노드보다 작지 않은 완전이진트리
-
최소 힙(Min Heap) : 최소 트리는 각 노드의 키 값이 자식 노드의 키 값보다 크지 않은(=작거나 같은) 완전이진트리
= 부모 노드가 항상 자식 노드보다 작지 않은 완전이진트리
완전 이진 트리 🌳
트리에 노드를 삽입할 때 항상 왼쪽부터 차례대로 삽입하는 트리
최대 힙 구현
- 최대 힙에서의 삽입
삽입되는 원소의 정확한 위치를 결정하기 위해, 트리의 새 노드에 삽입하여 루트쪽으로 올라가며 알맞은 위치를 찾는다.
부모 노드와 삽입한 노드의 키 값을 비교하여 부모 노드보다 작지 않을 경우 위치를 교환하며 루트쪽으로 올라간다.
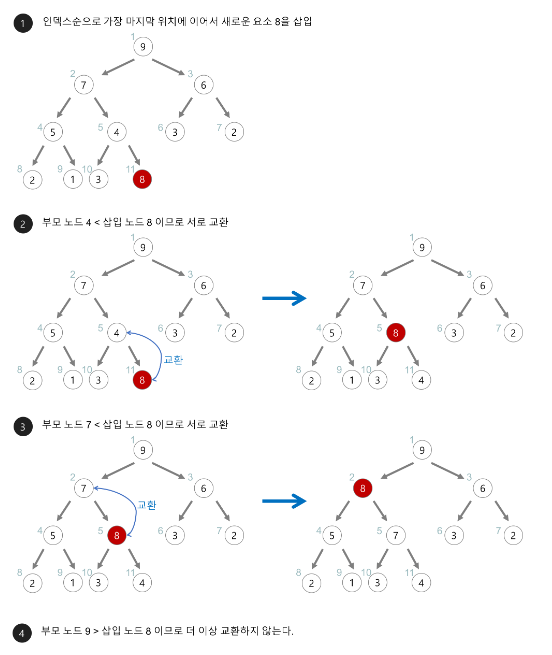
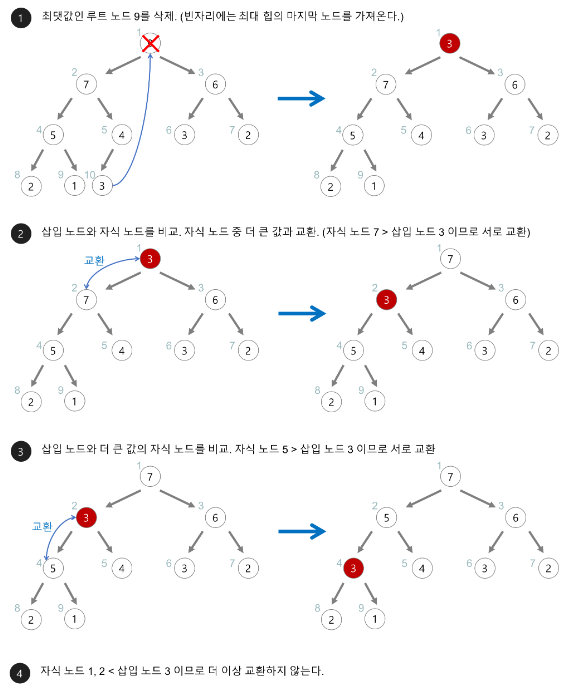
- 최대 힙에서의 삭제
최대 힙에서 원소를 삭제할 때에는 최대값인 루트 노드가 삭제된다.
삭제된 루트 노드의 위치에 힙의 마지막 노드를 이동시킨다.
삽입된 노드와 자식 노드의 키 값을 비교하여 자식 노드보다 작을 경우 위치를 교환하며 말단 노드쪽으로 내려가며 알맞은 위치를 찾는다.
출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
힙 정렬이 유용한 경우
1) 가장 크거나 가장 작은 값을 구할 때
가장 큰 값을 구하는 경우 : 최대 힙의 루트
가장 작은 값을 구하는 경우 : 최소 힙의 루트
2) 최대 k 만큼 떨어진 요소들을 정렬할 때
삽입정렬보다 더욱 개선된 결과를 얻어낼 수 있음

