그레이디언트 기반 최적화(신경망의 엔진)
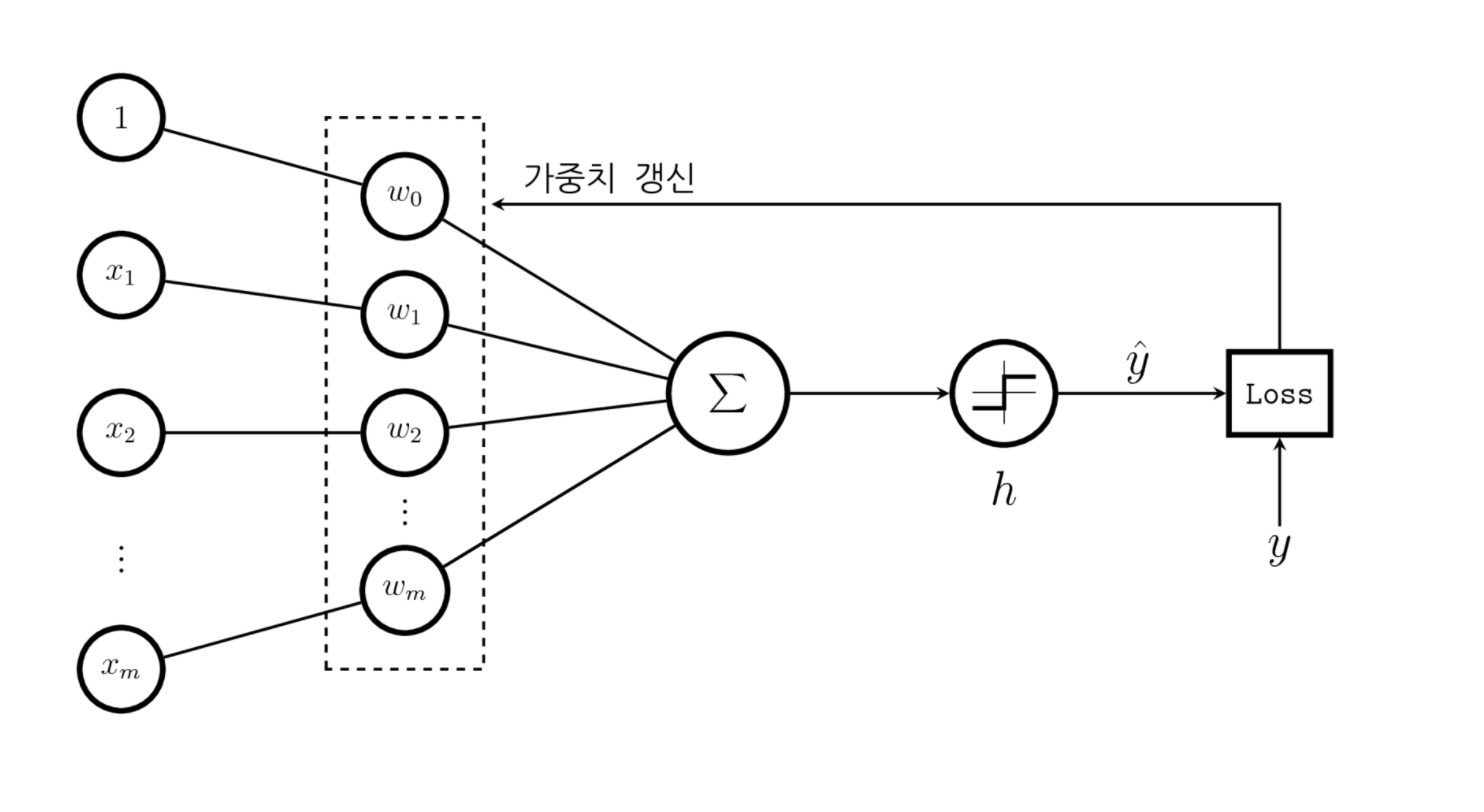
각 층의 입력데이터
output = relu(dot(W, input)+b)
- W(tensor)와 b(bias)는 층의 가중치, 훈련파라미터
- 초기의 가중치행렬은 무작위 초기화 = 의미없는 representation
- 훈련, 훈련 반복 루트를 통해 가중치가 점진적으로 조정(optimizing)
- 손실점수가 낮아질때까지 반복
- 의미 있는 representation을 출력할 때 까지 반복
가중치 업데이트를 하는 방법: 경사하강법
모델의 가중치를 업데이트 하려고 할 때 그 값을 증가할 지, 감소할 지 알 수 있는 효과적인 방법
= 경사하강법
- 함수가 학습될 바를 정의한 비용함수의 값이 최소로 하기 위해 가중치를 업데이트 하기 위한 알고리즘
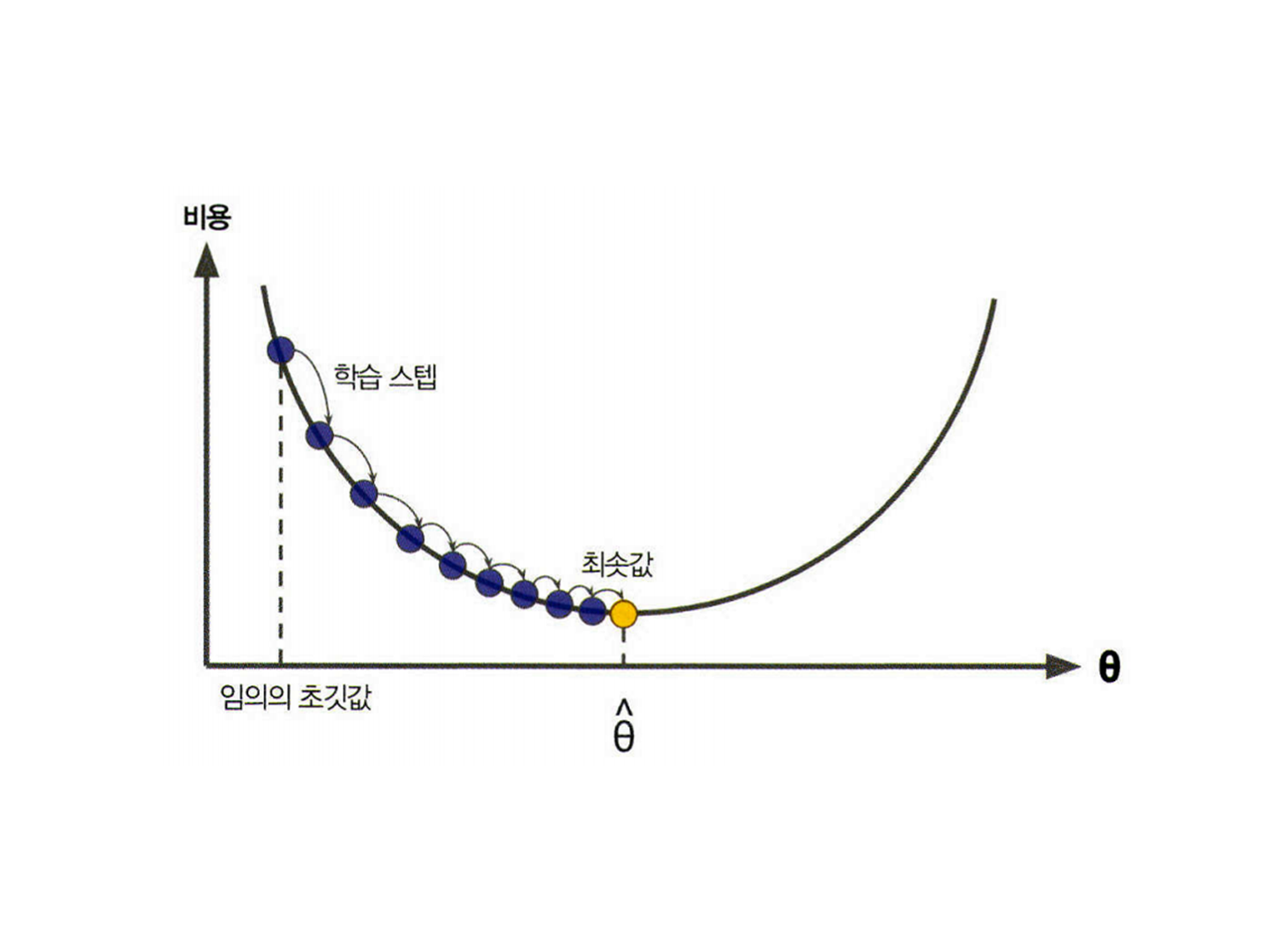
1) 도함수 이해하기
🔸 모델에 사용하는 모든 함수는 연속적이고 매끄러운 방식으로 변환된다. 이를 미분 가능하다고 말한다.
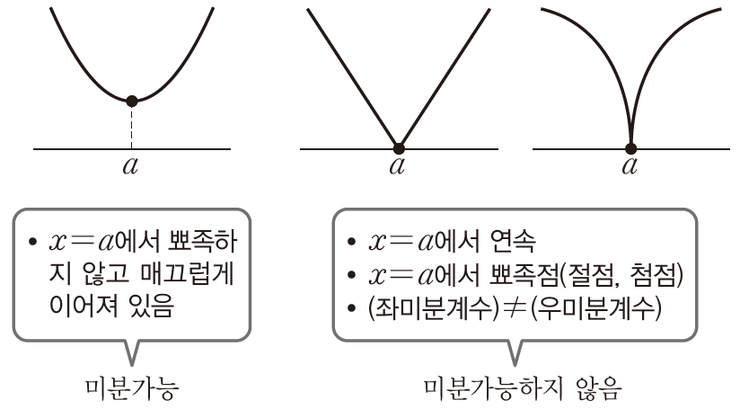
🔸 미분가능한 함수에서, 각 한 점에 대한 접선의 기울기를 미분계수라고 한다. (자세한 수학적 내용은 다루지 않음)
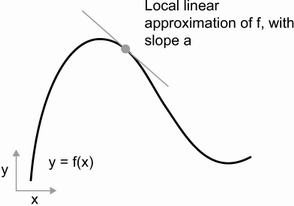
🔸 미분계수를 일일이 구하지 않고 함수로 표현한 것이 도함수
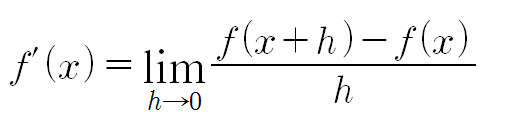
- 예시1: 의 도함수
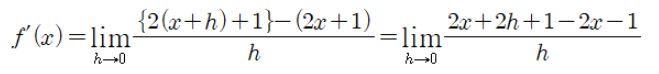
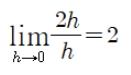
- 도함수는
- 도함수는
- 예시2:
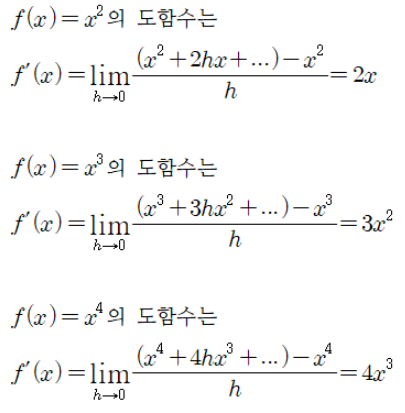
- 이를 적용한다면, 의 도함수는
- 이를 적용한다면, 의 도함수는
🔸 미분가능하다는 말은 도함수를 유도할 수 있다는 의미이며, 이는 의 값을 최소화 하는 값을 찾는 최적화에 매우 강력한 도구가 된다.
2) 그레이디언트(Gradient)
- 텐서연산의 도함수 = 그레이디언트
- 텐서 함수의 그레이디언트는 그 함수가 설명하는 다차원 표면의 곡률을 나타낸다.
🔸 머신러닝 기반의 예
- 모델가중치 W를 사용한 x추측
y_pred = dot(W,x) - 예측이 얼마나 벗어났는 지 추정
loss_value = loss(y_pred, y_true)
- f는 W가 변화할 때 손실 값이 형성하는 곡선설명
loss_value = f(W)
ex)
grad(loss_value(f(W0)), W0)
→ W0의 위치에서 loss_value(f(W))의 그레이디언트를 표현
→ W0에서 가장 크게 변화되는 방향과 그 방향의 기울기
🔸 편도함수
grad( f(W), W ) = grad_ij( f(W), w_ij )의 조합
grad_ij를 W[ i, j ]에 대한 f의 편도함수
3) 확률적 경사 하강법(SGD)
🔸 미니배치 확률적 경사 하강법(mini batch stochastic gradient)
- 훈련샘플 배치와 이에 상응하는 타깃값(실제값) _true를 추출
- 로 모델을 실행, 예측값 _pred를 구한다 ( 정방향 패스 )
- 타깃값과 예측값의 오차(_true, _pred)를 측정하여 손실 계산
- 손실함수의 그레이디언트를 계산( 역방향 패스 )
- 그레이디언트의 반대방향으로 파라미터를 이동( W -= learning_rate * gradient )
- 여기서 learning rate(학습률: 가중치가 변경되는 정도)은 경사하강법의 속도를 조정하는 역할
- '확률적': 각 배치 데이터가 무작위로 선택됨
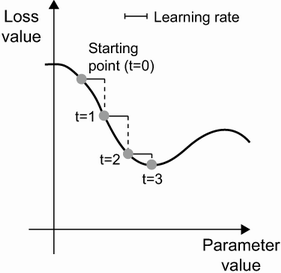
- 적절한 'learning rate' 필요, 너무 작으면 많은 반복작업이 필요하고, 너무 크면 완전 임의의 위치로 이동시킬수 있음
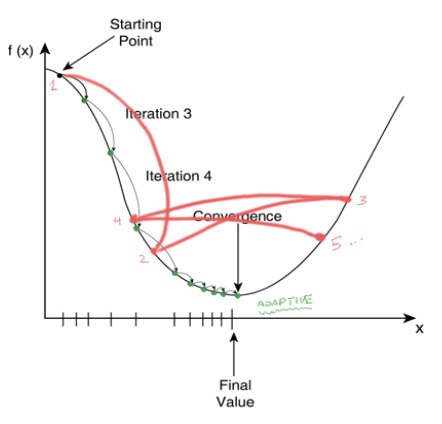
🔸 경사하강법의 시각화(2D 손실함수)
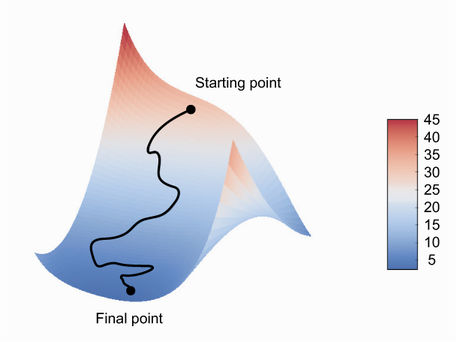
🔸 참고: 가중치 업데이트시 현재 그레이디언트 값만 보지 않고 이전에 업데이트된 가중치를 다른 방식으로 고려하는 SGD의 변종
= 모멘텀(momentum)
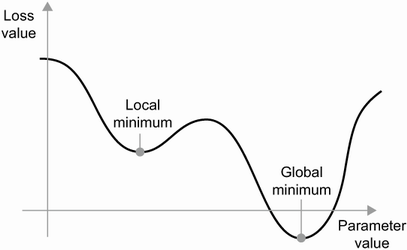
- 어떤 파라미터값에서 그 지역 최소값에 도달: 만족스런 손실값(전역 최솟값)이 되지 못할 수 있다
- 작은 공을 굴리듯 과거의 하강하는 가속도로 인한 현재속도를 고려하여 공을 움직이함
- 다시 변화하는 파라미터 값에서 만족하는 최솟값을 찾는 과정
4) 도함수의 연결: 역전파 알고리즘
🔸 연쇄법칙
-
미적분의 연쇄 법칙을 사용하면 연결된 함수의 도함수를 구할 수 있다.
-
신경망의 그레이디언트 값을 계산하는 데 연쇄법칙을 적용하는 것이 역전파 알고리즘이다.
- ex)
Dense(relu) Dense(softmax) 두개의 층으로 된 모델에서 loss_vallue = loss(y_true, softmax(dot(relu(dot(inputs, W1) + b1), W2) + b2) -
두함수를 연결한 f g 는
-
= *
-
🔸 그림 설명
-
2개의 층으로 구성된 모델의 계산 그래프
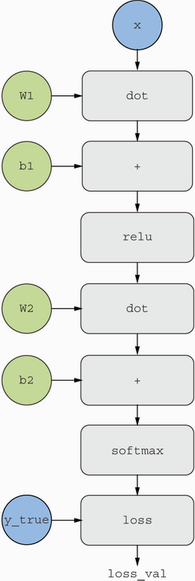
-
간단한 계산 그래프(정방향 패스)
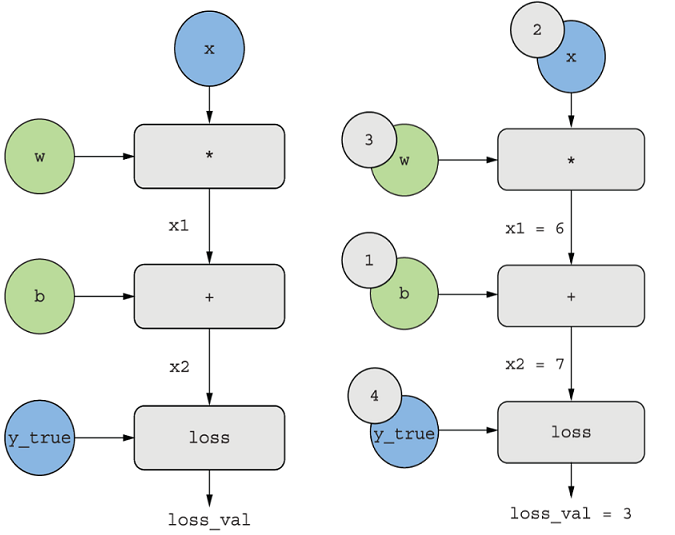
-
역방향 패스
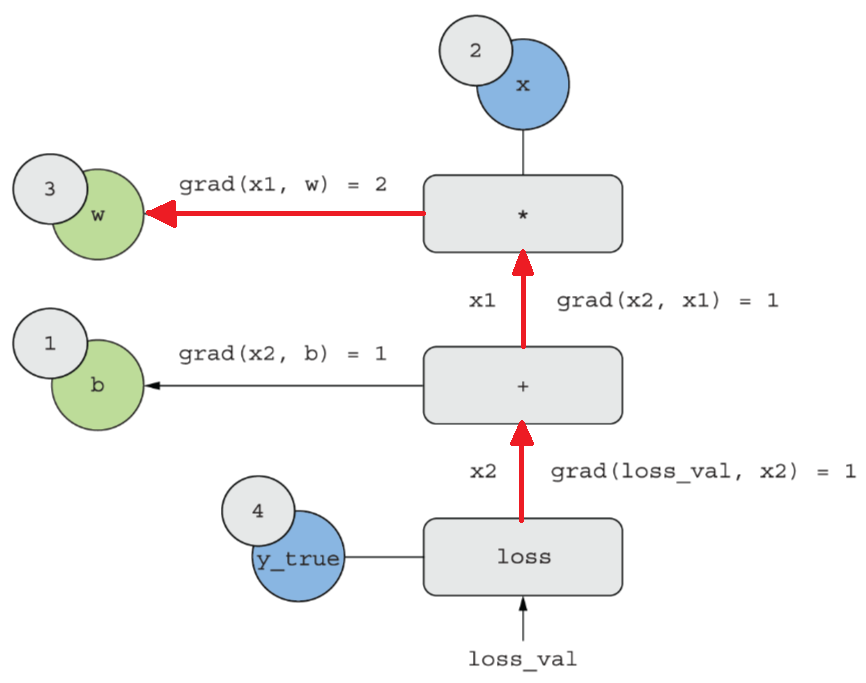
①
- 변수를 w로 두고 미분:
- grad(x1,w) = x
- grad(x1,w) = 2
- 변수를 x로 두고 미분(참고):
②
-
-
grad(x2,x1) = 1
③
-
-
grad(loss_val,x2)=1
④ 원하는 값
- grad(loss_val, w) = 1 * 1 * 2 = 2
- grad(loss_val, b) = 1 * 1 = 1
