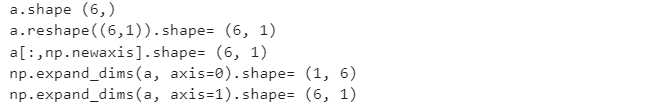딥러닝이란?
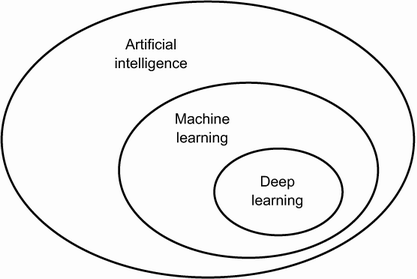
인공지능
보통의 사람이 수행하는 지능적인 작업을 자동화 하기 위한 연구활동
머신러닝
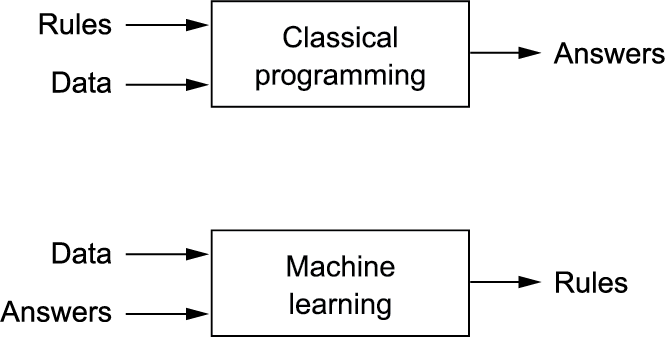
이미지분류, 음성인식, 언어 번역 같은 복잡하고 불분명한 문제를 해결하기 위한 명확한 규칙을 찾기 위한 연구
- 훈련(training): 데이터와 해답을 가지고 규칙을 찾는다
-
경험적 발견에 의해 주도되는 매우 실천적인 분야
-
머신러닝의 구성
- 입력데이터
- 기대 출력(labels)
- 성능측정 방법: 측정값은 교정을 위한 신호로 측정방법을 변환하면서 측정값을 수정해 나가는 단계를 학습(learning)이라고 한다.
딥러닝과 머신러닝
공통 핵심 문제
데이터가 의미있도록 변환 하는것
= 데이터의 유용한 representation을 학습하는 것
딥러닝에서의 'DEEP'
연속된 층(layers)(=연속된 필터(filter))을 거치면서 점진적으로 의미있는 representation을 찾아가는 것
따라서 계층적 표현학습, 층 기반 표현학습이 될 수 있다.
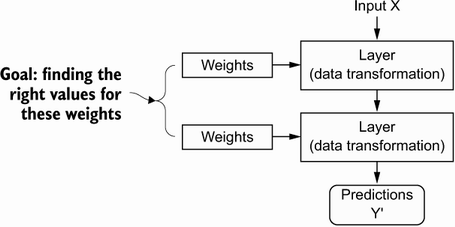
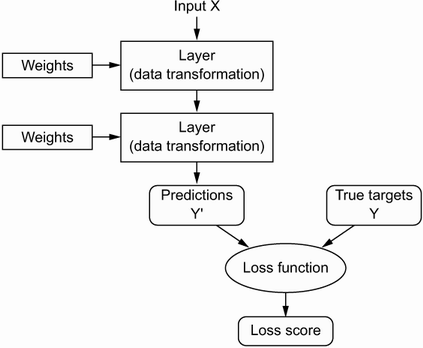
딥러닝의 작동원리(구성)
🔸 InputX: input_tensor(데이터)
🔸 Layers(텐서연산):
- 층이 데이터를 처리하는 방식
- 가중치(weight)와 편향(bias)
- 초기 가중치 행렬은 무작위 초기화
- 학습 목표는 손실을 줄일 수 있는 적절한 가중치 찾기
🔸 model-fit-prediction
- 모델의 성능을 측정(출력이 기대하는 것보다 얼마나 벗어났는지 측정)
- 손실함수(loss function) = 목적함수, 비용함수
- 손실함수의 설정은 model을 compile메서드로 호출하여 실행
- model.compile(loss = '...', )
- 손실함수의 설정은 model을 compile메서드로 호출하여 실행
- 예측측정(prediction): 타깃값(True targets)과 오류값으로 손실점수계산
🔸 optimizer(옵티마이저)
- 손실점수를 반영한 가중치 업데이트
(성능을 향상시키기 위해 입력된 데이터를 기반으로 모델을 업데이트) - 이 과정에서 뒤에서부터 그 오차의 값이 전파되며 이를 역전파(Backpropagation) 라고 한다.
- 옵티마이저는 model을 compile메서드로 호출하여 실행
- model.compile(optimizer = '...', )
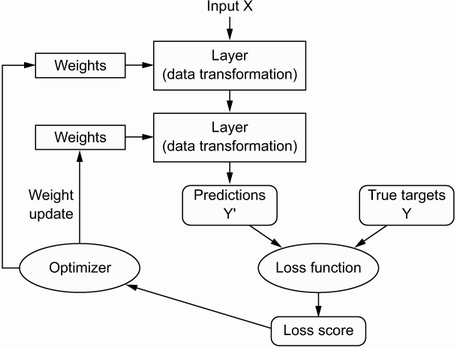
🔸 위의 과정이 반복되는 것이 훈련반복(training loop)
- 훈련 반복은 위의 model을 fit메서드로 호출하여 훈련을 반복하는 데 각 반복횟수를 epoch로 지정한다.
- model.fit(inputs, targets, epochs = ..., batch_size=...)
데이터 표현: 텐서
🔸 텐서(tensor)
- 기본 데이터 구조
- 임의의 차원 개수를 가지는 행렬의 일반화된 모습
- 차원(dimension) = 축(axis)
- 텐서 차원의 개수를 랭크(rank)라고 부르기도 함
🔸 참고 :
- 클래스(class): 분류문제에서의 카테고리
- 샘플(sample): 데이터
- 레이블(label): 특정 샘플의 클래스
랭크에 따른 텐서
1) 스칼라(랭크-0 텐서)
숫자 한개의 값
2) 벡터(랭크-1 텐서)
1차원 배열
3) 행렬(랭크-2 텐서)
2차원 배열
(samples, features)
4) 랭크-3 텐서 ~ 랭크-5 텐서
🔸 3차원 배열: 시계열 데이터, 시퀀스 데이터
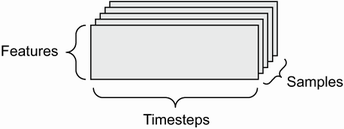
- (samples, timesteps, features)
- ex) 주식 가격 데이터 셋, 트윗 데이터셋
🔸 4차원 배열: 이미지 데이터
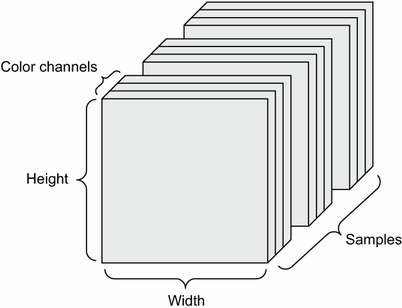
- (sample, height, width, channels)
- 채널 마지막(channel-last):(samples, height, width, color_depth)
- 채널 우선(channel-first):(samples, color_depth, height, width)
- color depth: 흑백은 1, 컬러는 3
🔸 5차원 배열: 동영상
- (sample, frame, height, width, channels)
- frame은 이미지의 연속된 길이
텐서의 핵심 속성
- ndim: 축의 개수(rank)
- shape: 크기
- dtype: 데이터 타입
- unit8 :unsigned int 8bit
- 1byte만큼의 정수표현 가능 (2**8 = 256)
- unsigned는 1byte 전부를 숫자로 표현, 부호 할당x
- unit8 :unsigned int 8bit
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()print(train_images.ndim)
print(train_images.shape)
print(train_images.dtype)3 (60000, 28, 28) dtype('uint8')
텐서 조작하기: 슬라이싱
slice1 = train_images[:100]
slice2 = train_images[100:200]
slice3 = train_images[:100,:,:]
slice4 = train_images[:,14:,14:]print(slice1.shape)
print(slice2.shape)
print(slice3.shape)
print(slice4.shape)배치 데이터
딥러닝 모델은 한번에 전체 데이터 셋을 처리하지 않는다.
데이터를 작은 배치(batch)로 나누는 데, 배치데이터의 첫번째 축을 배치 축(batch axis), 배치 차원(batch dimension)이라고 부른다.
🔸 n번째 배치를 구하는 샘플: batch size = 128
for i in range(round(len(train_images)/128)):
globals()[f'batch_{i}']= train_images[128*i:128*(i+1)]
batch_100.shape
(128, 28, 28)
텐서 연산(신경망 톱니바퀴)
- 텐서 연산을 통해 텐서를 조작한다. 이는 기하학적 변형을 적용하므로 기하학적 해석이 가능하다
케라스의 층을 만드는 코드
keras.layers.Dense(512, activation = 'relu')- layers: 층, 필터
- Dense: 조밀하게 연결된 신경망(densely connected)
- 512(임의의 값): 그 층에서 출력되는 뉴런의 수
- activation: 입력된 데이터의 가중 합을 출력신호로 변환하는 함수
output = relu(dot(W, input)+b)
- input tensor와 가중치(W tensor)의 점곱: 곱해서 더한 값
- 편항(벡터값 b)을 더함: 오차들을 감안하기 위함
- relu연산
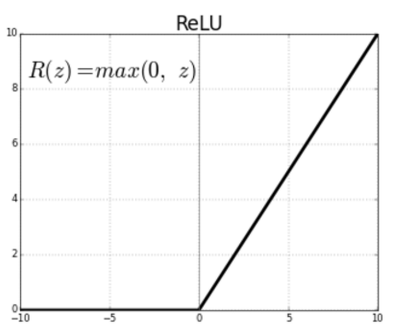
참고1: relu
relu(x) = np.maxium(0,x)
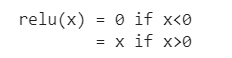
참고2: sigmoid
sigmoid(x) = 1/1+(e**-x)
sigmoid(x) = 1/1+np.exp(-x)
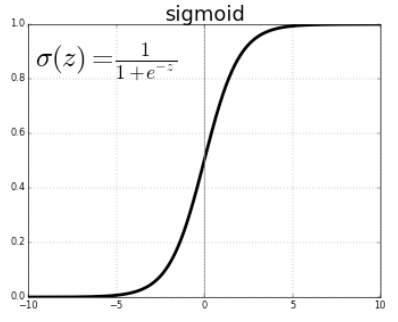
- 0과 1사이의 그래프, 중앙값은 1/2
- e = 2.71818...
- e그래프 참고
1) 브로드캐스팅
- 큰 텐서의 ndim에 맞도록 작은 텐서에 축을 추가
- 작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복
x = np.random.random((32,10))
y = np.random.random((10,))# 축 추가
y = np.expand_dims(y,axis=0)
# 반복
y = np.concatenate([y]*32,axis=0)
print(x.shape, y.shape)
(32, 10) (32, 10)
🔸 축을 추가하는 방법
- reshape
- [ : , np.newaxis] or [np.newaxis , : ]
- np.expand_dims(x, axis=0) or np.expand_dims(x, axis=1)
2) 텐서곱셈 이해하기
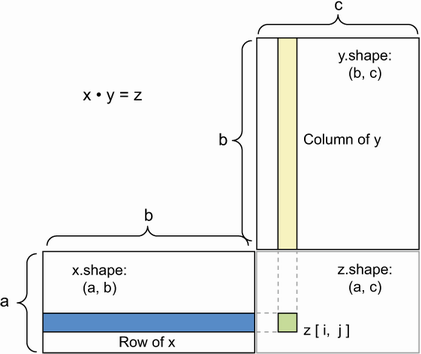
- 텐서 곱셈 또는 점곱
- 원소개수가 같은 벡터끼리 점곱할 수 있다.
- x의 두번째 차원이 y의 첫번째 차원과 같아야함
- np.dot(row_x,column_y)
- 참고 코드
def naive_matrix_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 2
# x의 두번째 차원이 y의 첫번째 차원과 같아야함
assert x.shape[1] == y.shape[0]
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
for j in range(y.shape[1]):
row_x = x[i, :]
column_y = y[:, j]
z[i, j] = naive_vector_dot(row_x, column_y)
return z3) 텐서 크기변환
- 특정 크기에 맞게 열과 행을 재배열
- 자주 사용하는 변환: 전치(transpose)
🔸 shape 이해
a= np.random.randint(0,5,6)print('a.shape',a.shape)
print('a.reshape((6,1)).shape=',a.reshape((6,1)).shape)
print('a[:,np.newaxis].shape=',a[:,np.newaxis].shape)
print('np.expand_dims(a, axis=0).shape=',np.expand_dims(a, axis=0).shape)
print('np.expand_dims(a, axis=1).shape=',np.expand_dims(a, axis=1).shape)4) 텐서연산의 기하학적 해석
이동, 회전, 크기변경, 기울이기 등과 같은 기본적 기하학적 연산은 탠서 연산으로 표현 가능
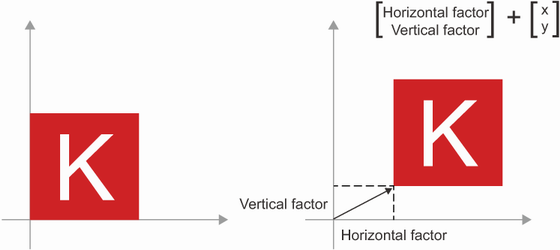
🔸 이동
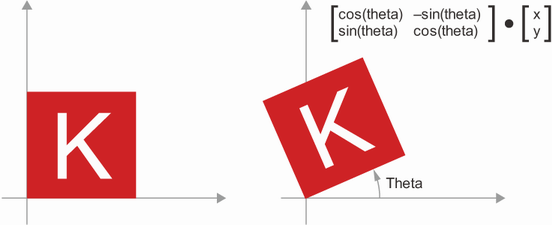
🔸 회전
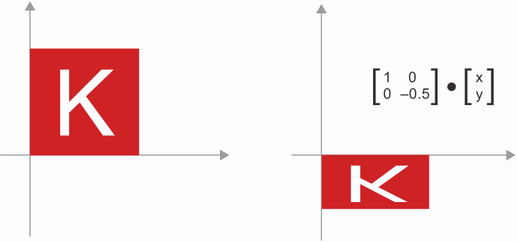
🔸 크기변경
🔸 아핀변환: 선형변환과 이동의 조합
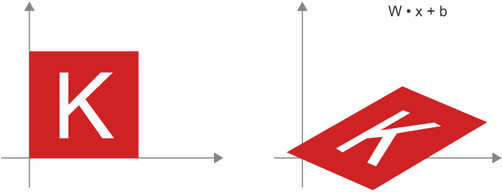
🔸 relu activation을 사용하는 Dense층
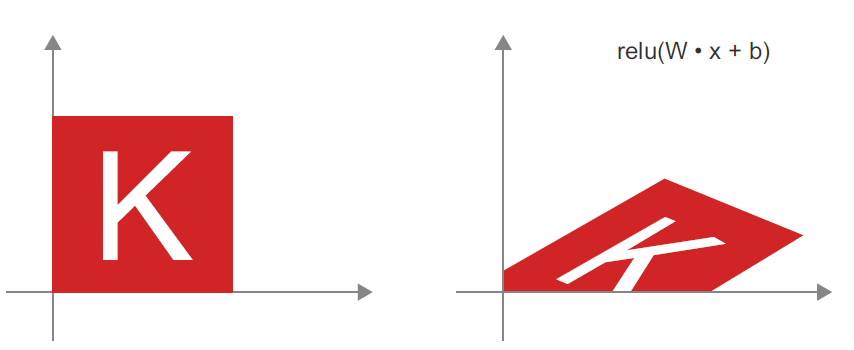
기초적인 연산을 길게 연결하여 복잡한 기하학적 변환을 조금씩 분해하는 방식이 딥러닝의 방식(종이공을 펼치기위한 전략)