Evaluating MCMC models

해당 문서는 Coursera 강의 Bayesian Statistics: Techniques and Models
를 보고 공부한 것을 정리한 노트입니다.

---

1. JAGS model

지난 시간엔 jags를 파이썬에서 실행하는 방법을 알아보았다.
이제 모델의 실행 결과를 자세히 보도록 하자.

지난 게시물 에서 썼던 코드를 그대로 가져오겠다.

import pyjags
import numpy as np
import pandas as pd
import seaborn as sns

anscombe = sns.load_dataset('anscombe')
mydf = anscombe[anscombe['dataset']=='I']

y = mydf['y'].values
X = mydf['x'].values

jags_model_string = ''' 
model {
  for (i in 1:n) {
    y[i] ~ dnorm(mean[i], 1/sig2)
    mean[i] <- int + b*X[i]
  }
  b ~ dnorm(0, 1e-5)
  int ~ dnorm(0, 1e-5)
  sig2 = 1.0
}
'''

jags_data = {'y':y, 'X':X, 'n':len(mydf)} # jags_data에 데이터 할당
parameters = ['int', 'b']

jags_model = pyjags.Model(code=jags_model_string, 
                          data=jags_data, 
                          chains=3)

jags_model.sample(1000, vars=[])

n_iter = 3000
jags_samples_from_model = jags_model.sample(n_iter, vars=parameters)

위 과정의 bayesian 모델은 다음과 같다.

$y_i \sim N(\mu_i,1)$
$\mu_i = b_0 + b_1 x_i$
$b_1 \sim N(0, 1e+5)$
$b_0 \sim N(0, 1e+5)$

$b_1$과 $b_0$에 대한 사전분포는 분산이 매우 큰 non-informative prior로 가정해 주었다.
JAGS에서는 dnorm을 정의할 때 평균과 $\tau$값이 argument로 들어가기 때문에 $\sigma^2$의 역수의 값을 넣어줘야 한다.

과정을 간단히 요약하자면
1. seaborn의 anscombe 데이터를 가져온다.
2. y값이 정규분포를 따르는 단순선형회귀 모델을 정의한다.
3. 각각의 파라미터들의 사전분포를 정의한다.
3. 1000번의 burn-in iteration을 수행한다.
4. 3000번의 iteration을 통해 파라미터 각각의 Monte-Carlo 샘플을 뽑는다.

2. Convergence

지난 게시물에서 말했듯이 az.plot_trace함수로 모델의 수렴성을 볼 수 있다.

import arviz as az
idata_jags_model = az.from_pyjags(jags_samples_from_model)
az.plot_trace(idata_jags_model)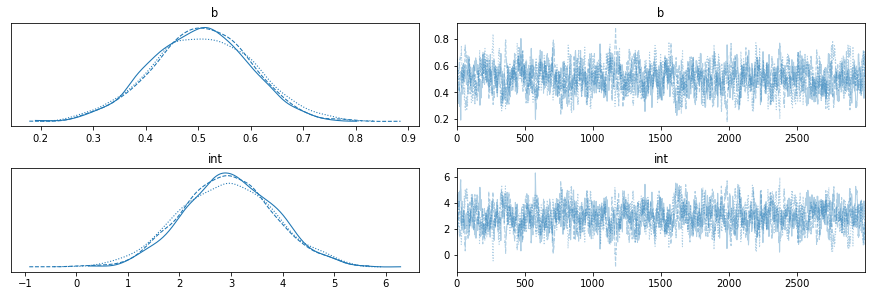

파라미터 당 3개의 독립적인 chain을 돌렸으니 파라미터 당 3개의 분포 그림이 있다.
오른쪽은 파라미터의 수렴성을 볼 수 있는 부분이다. 우리는 1000번의 burn-in iteration을 수행해서 안정적인(것으로 보이는) 분포를 얻었다. 만약 burn-in을 수행하지 않는다면 어떻게 될까?

burn-in을 수행하지 않고 3000번 iteration을 돌렸다.

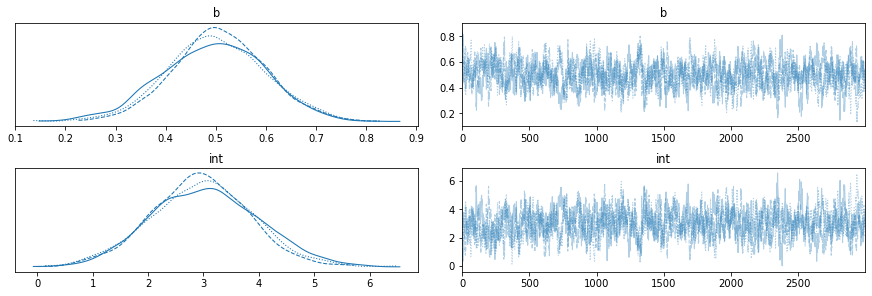
이 task에서는 burn-in이 크게 상관 있어 보이지는 않는다. 하지만 각각의 chain의 수렴 속도가 달라 분포에서 차이가 큼을 볼 수 있다. 타겟 데이터가 커질수록 수렴 속도는 더 큰 차이를 보일 것이다.

MCMC로 수집된 표본의 수렴성을 측정해 볼 수 있는 검정 방법이 있다.
바로 gelman-rubin diagnostic이다.

해당 검정은

az.rhat(idata_jags_model)

코드로 실행해 볼 수 있다. 파라미터당 rhat 값이 1에 가까울수록 표본의 분포가 수렴성을 띠고 있다고 볼 수 있다.

3. Autocorrelation

MCMC를 시행한 후 iteration의 표본이 모두 독립적인 것은 아니다. marcov chain의 기본 가정으로 인해 각 iteration의 샘플은 그 이전 샘플에 종속적이다. 그렇다면 n iteration 이전 샘플에 대해서도 어느 정도 correlation이 존재할 수 있다. 이것을 autocorrelation plot으로 나타낼 수 있다.

az.plot_autocorr(idata_jags_model, combined=True)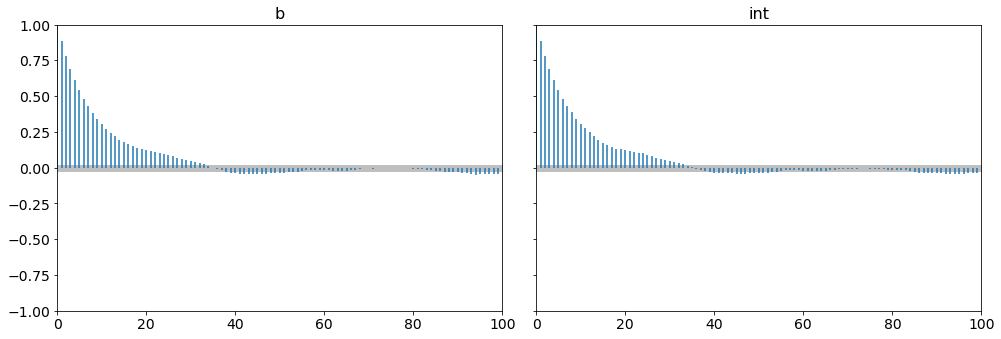

correlation은 정의에 의해 -1, 1사이의 값이다. 값이 1에 가까우면 양의 상관관계가 있고, -1에 가까우면 음의 상관관계가 있다고 본다. correlation plot을 보면 MCMC의 특정 iteration의 sample이 30~40 lags까지 상관관계가 존재하는 것을 확인할 수 있다.

상관관계는 MCMC sampling에서 아주 중요한 문제이다. marcov chain의 상관관계가 높다면 iteration에 비해 우리가 얻을 수 있는 독립적인 sample이 줄어들게 되고, 그렇다면 우리가 획득할수 있는 정보량(information gain) 또한 적어진다.

4. Effective Sample Size

위의 개념을 그대로 적용시킨 개념이 ESS(effective sample size)이다. 한마디로 말해서 stationary distribution에서 서로 독립인 sample이 몇 개나 수집되는가? 이다.

ESS는 pyjags에서 해당 코드로 얻을 수 있다.

az.ess(idata_jags_model)

만약 우리가 원하는 것이 사후분포의 평균을 추정하는 것이라면 몇 백개~ 몇 천개의 ESS로도 추정이 가능할 수 있다. 하지만 95% posterior interval을 추정하기 위해서는 더 많은 ESS가 필요하다.

그러면 수리적으로 얼마나 많은 ESS가 있어야 interval을 추정할 수 있는가?
raftery-lewis diagnostic을 활용하면 marcov chain에서 필요한 ESS의 개수를 구할 수 있다. 다만 해당 검정을 pyjags에서 실행하는 방법을 찾지 못했다. R에서는 rjags라이브러리의 raftery.diagfunction으로 실행시킬 수 있다.

---