Discriminant Analysis

Logistic regression과 다른 방법으로도 classification을 진행할 수 있다.

각 class 별 X의 distribution을 modeling하고, Bayes theorem을 적용해 $Pr(Y\mid X)$를 얻는다. 이를 discriminant analysis 방법이라고 한다.

Bayes Theorem for Classification

$X=x$ 일 때, $Y=k$에 대한 conditional probability에 대해 Bayes theorem을 적용하면 다음과 같이 표현할 수 있다.

$Pr(Y = k)$와 $Pr(X = x)$는 data를 통해 쉽게 알 수 있다. 또한, condition이 $X$일 때보다 $Y$일 경우에 각 condition 별 data sample의 개수가 훨씬 많아지기 때문에 distribution을 추정하기 용이하다.

위 식을 다음과 같이 표현하자.

• $f_k(x) = \Pr(X = x \mid Y = k)$: density for X in class k
  • 여기서는 gaussian distribution으로 가정
• $\pi_k(x) = \Pr(Y = k)$: prior probability for class k

이를 이용하면, 새로운 data point $X=x$에 대해 다음과 같이 class를 정할 수 있다.

1. 각 k에 대해 $\pi_k f_k(x)$를 계산
2. 가장 높은 값을 갖는 class k로 x를 할당

Discriminant Analysis vs. Logistic Regression

현실에서는 별로 그럴 일은 없지만, data가 well-seperated 되어있는 경우에 logistic regression model은 unstable하다 (결과의 차이는 없을지라도). 하지만 discriminant analysis을 사용하면 안정적인 model을 가질 수 있다.

또한, X의 distribution이 어느정도 예측이 되는 경우(특히 normal에 가까울 때)에는 X의 density를 보다 정확하게 가정할 수 있으므로 더욱 안정적인 model을 만들 수 있다.

추가적으로 Multiclass classification 문제에서 logistic regression에 비해 보다 low-dimensional view를 제공할 수 있다.

Linear Discriminant Analysis (LDA)

When $p=1$

$f_k(x)$가 Gaussian density를 따르고 (Gaussian을 따른다고 가정하면 많은 부분에서 편리해진다), 모든 k에 대해 $\sigma_k=\sigma$라고 가정하자.

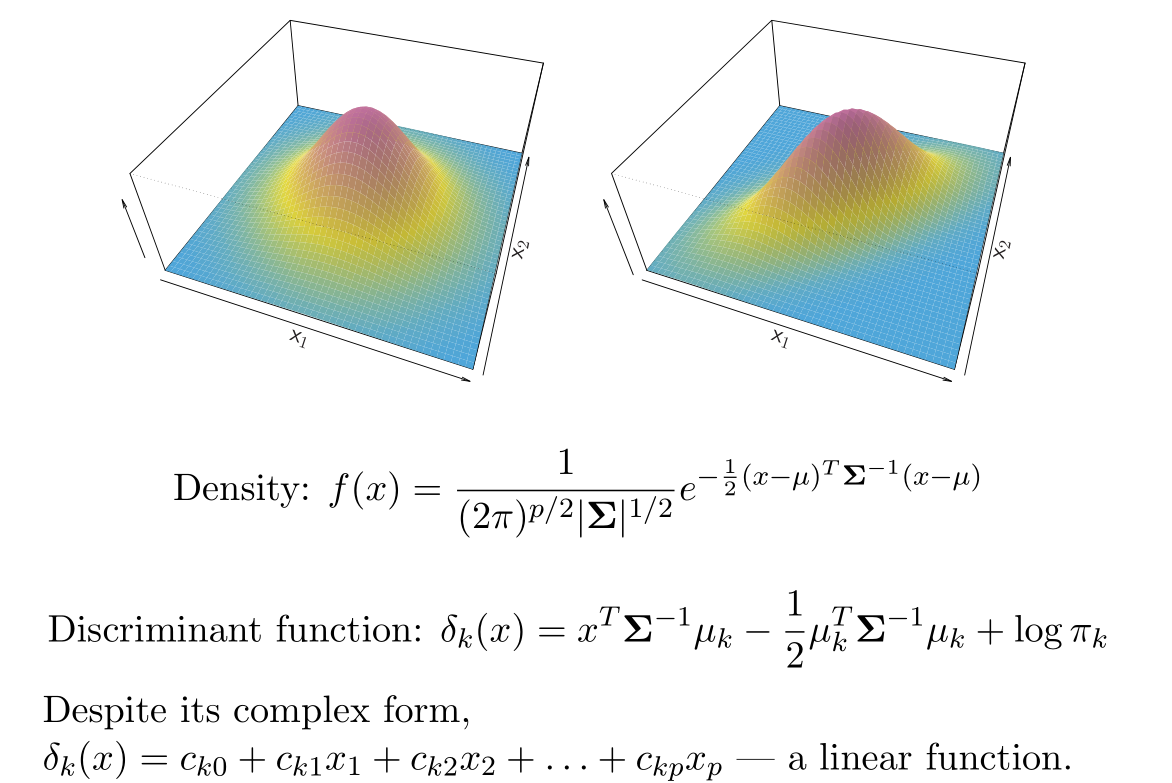
그렇다면, $p_k(x)=\Pr(Y = k \mid X = x)$는 다음과 같다.

위 식을 이용하면, 결국 새로운 data point $X=x$에 대해, discriminant score $\delta_k(x)$ 값이 가장 큰 k로 할당하는 것과 동일한 문제가 된다.

이 때, $\delta_k(x)$는 $x$의 linear function이 된다.

위와 같은 방식의 discriminant analysis를 linear discriminant analysis (LDA)라고 말한다.

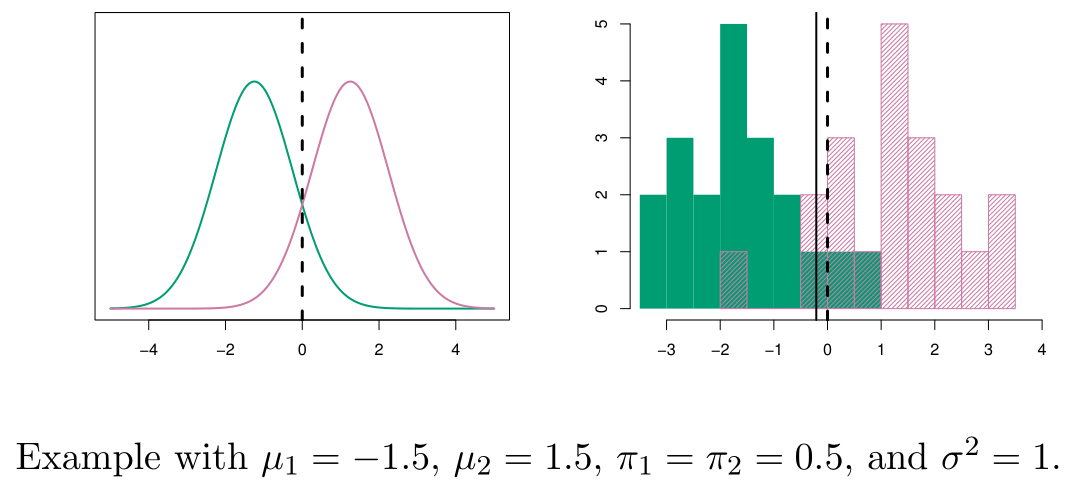
When $p>1$

아래는 $p=2$이고 $K=3$인 경우에 대한 LDA 예시 그림이다.

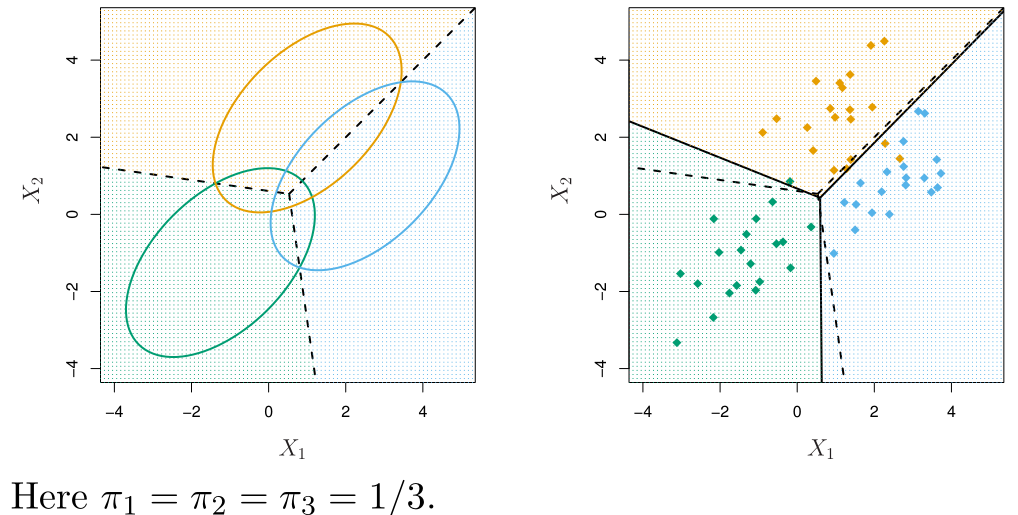
위 그림에서 점선은 Bayes decision boundaries 라고 불리며, 가장 적은 misclassification을 보장하는 boundary이다.

Other Forms of Discriminant Analysis

$f_k(x)$의 형태에 따라 다양한 discriminant analysis 방법이 존재한다.

Quadratic Discriminant Analysis (QDA)

만약, 각 class 별로 Gaussian이지만 variance가 다 다른 경우, quadratic discriminant analysis (QDA)이 된다.

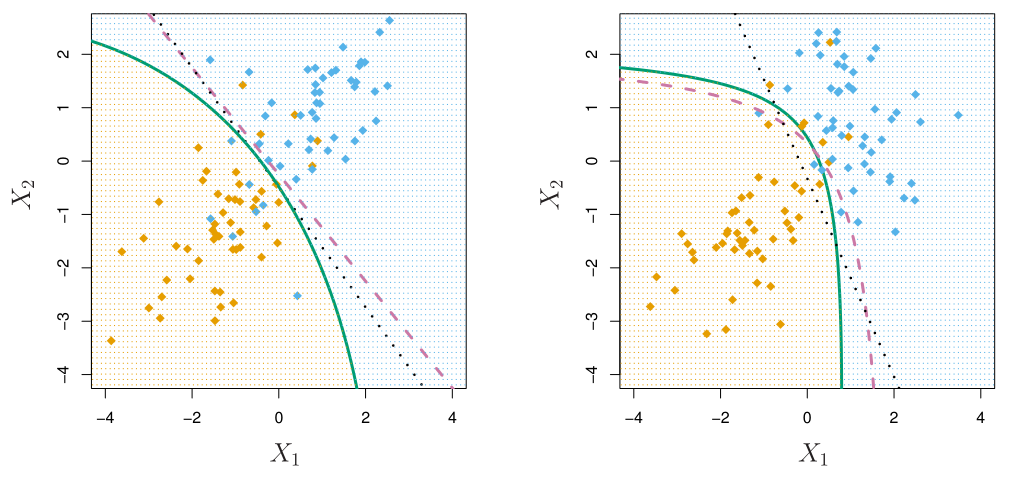
Naive Bayes

만약, 각 class에서 $X$들이 independent한 경우(condtional independence), 즉 $f_k(x) = \prod_{j=1}^p f_{jk}(x_j)$이면, naive Bayes classification model이 된다.

Naive Bayes는 feature의 개수가 매우 많을 때, 유용하게 사용된다.