Mathematics for Deep Learning

Roh's warehouse·2025년 9월 22일

Introduction to DL

목록 보기

2/17

Distributions

Logistic Sigmoid

\sigma(x) = \frac{1}{1+\exp(-x)}

Softplus Function

\zeta(x) = \log(1+\exp(x))

softened version of $x^+ = \max(0,x)$

Properties of Sigmoid

$\sigma(x) = \frac{1}{1 + \exp(-x)} = \frac{\exp(x)}{\exp(x) + \exp(0)}$
$\frac{d}{dx} \sigma(x) = \sigma(x)(1 - \sigma(x))$
$1 - \sigma(x) = \sigma(-x)$
$\log \sigma(x) = -\zeta(-x)$
$\frac{d}{dx} \zeta(x) = \sigma(x)$
$\forall x \in (0, 1), \; \sigma^{-1}(x) = \log \left( \frac{x}{1 - x} \right)$

Information Theory

Entropy

Information theory는 information이라는 개념에 대한 quantifying하는 것에 대한 학문이다. 여기서 가장 기본 개념은, 발생 확률이 낮은 event가 더 informative하다는 것이다.

어떤 event $x$ 이 가지고 있는 information quantity 또는 self-information은 event $x$ 가 발생할 확률 $P(x)$ 를 표현하기 위한 최소 bits 개수로, 다음과 같이 정의한다.

I(x) = -\log_2 P(x)

$P(x)$ 가 낮을수록 $I(x)$ 는 증가한다는 것을 알 수 있다.

이 때, entropy란 self-information의 expectation을 말하며, 다음과 같이 정의된다.

H(x) = E_{x \sim P} [I(x)] = -E_{x \sim P} [\log P(x)]

어떤 distribution에서 발생한 event의 information quantity의 기댓값이므로, 해당 distribution의 uncertainty 크기에 대한 measure로 볼 수 있다.

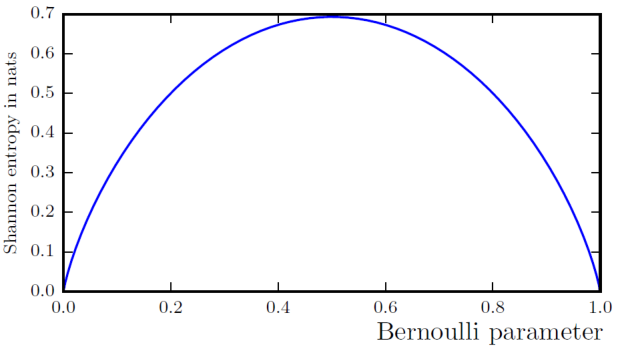
예를 들어, Bernoulli distribution을 고려하자. 이 때의 entropy는 다음과 같이 정의된다.

H(x) = -p\log p - (1-p) \log (1-p)

만약, distribution이 deterministic하다면, 즉 $p=0$ 또는 $p=1$ 이면, $H(x)$ 는 0이 된다 (여기서 $0\log 0 = 0$ 으로 고려).

반면에, 가장 uncertain 한 상황인 $p=0.5$ 인 경우, $H(x)$ 는 약 0.693 정도로 가장 큰 값을 갖는다.

KL Divergence

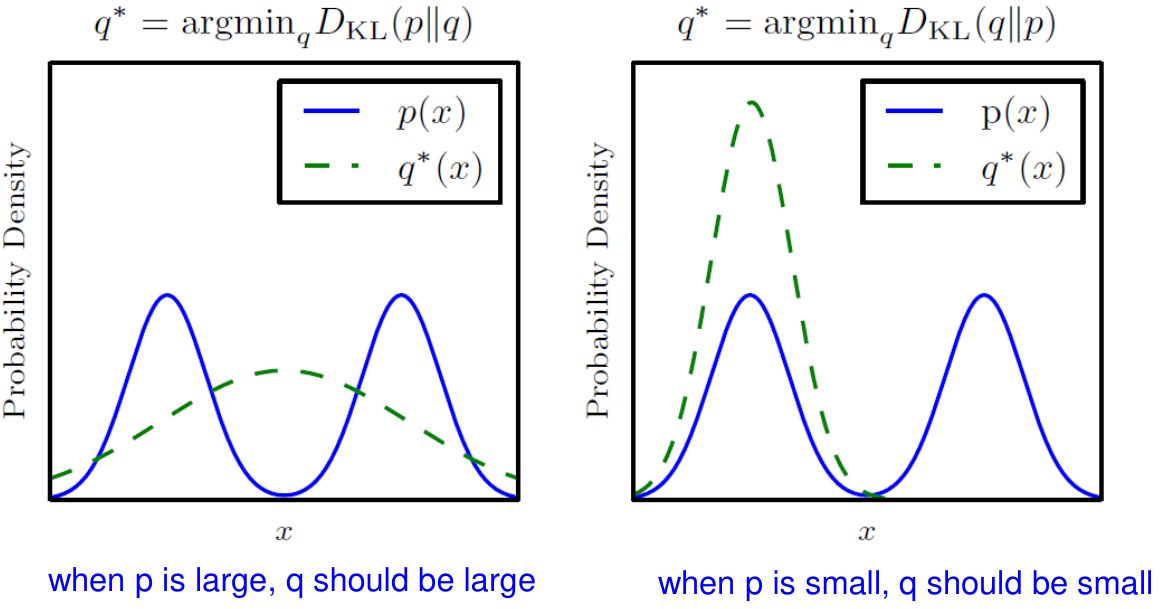
Kullback–Leibler divergence, 또는 KL divergence는 두 distribution에 대한 차이를 나타내는 비대칭적 지표이다.

D_{KL}(P \parallel Q) = E_{x \sim P} \left[ \log \frac{P(x)}{Q(x)} \right] = E_{x \sim P} \left[ \log P(x) - \log Q(x) \right]

$D_{KL}(P \parallel Q) = 0$ if and only if $P$ and $Q$ are the same.
Asymmetric: $D_{KL}(P \parallel Q) \ne D_{KL}(Q \parallel P)$

Cross-entropy

우리가 관심있는 것이 data의 distribution $P$ 라고 하자. 하지만, 일반적으로 우리는 $P$ 에 대해서는 알지 못한다. 따라서 우리는 $P$ 를 모사하는 model을 만들고 $P$ 에 대한 추정을 진행한다. 이 때, model의 (output에 대한) distribution을 $Q$ 라고 하자.