Non-Linear Regression Model

Roh's warehouse·2025년 9월 21일

Introduction to ML

목록 보기

12/19

현실의 data는 결코 linear하지 않지만, linear model은 interpretability에서 큰 장점을 가지고 있기에 자주 사용된다. 여기서는 기존 linear model에 non-linearity를 더해 accuracy와 interpretability를 모두 잡기위한 노력으로 개발된 방법론들을 소개한다.

Piecewise Polynomial

Polynomial Regression

Polynomial regression은 feature의 제곱수들을 새로운 feature로 가정하고 multiple linear regression을 적용한 것이다.

Degree- $d$ polynomial regression는 다음과 같다.

y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \cdots + \beta_d x_i^d + \varepsilon_i

위 식을 통해, logistic regression도 자연스럽게 다음과 같이 유도된다.

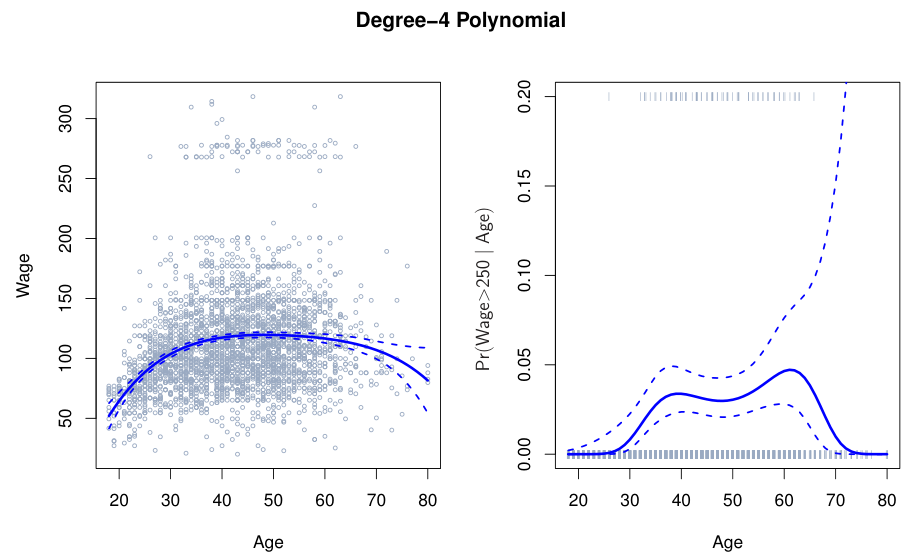
p(Y=y_i|X=x_i)=\frac{\exp(\beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \cdots + \beta_d x_i^d)}{1+\exp(\beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \cdots + \beta_d x_i^d)}

Polynomial regression은 tail behavior가 좋지않다. 따라서, extrapolation 성능이 매우 나쁘다.

Step Function

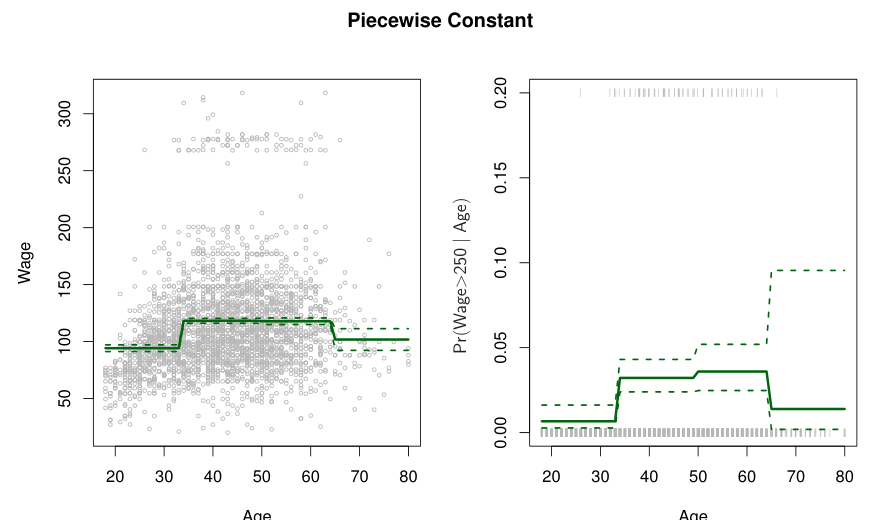
Feature의 범위에 따라 다른 값을 할당하는 step function으로도 non-linearity를 표현할 수 있다.

C_1(X) = I(X < 35), \; C_2(X) = I(35 \leq X < 50),\; \dots,\; C_4(X) = I(X \geq 65)

Piecewise Polynomial

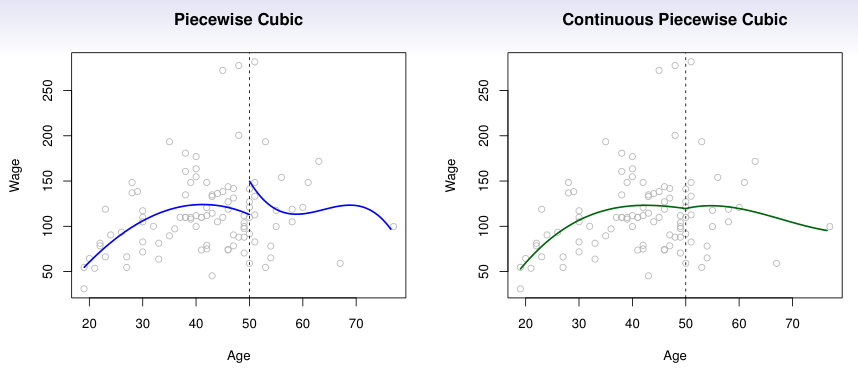
Piecewise polynomial은 polynomial regression과 step function을 합한 것으로, feature를 구간 별로 나눈 후, 구간 별로 다른 polynomial regression을 적용한 것이다.

y_i = \begin{cases} \beta_{01} + \beta_{11}x_i + \beta_{21}x_i^2 + \beta_{31}x_i^3 + \varepsilon_i & \text{if } x_i < c \\ \beta_{02} + \beta_{12}x_i + \beta_{22}x_i^2 + \beta_{32}x_i^3 + \varepsilon_i & \text{if } x_i \geq c \end{cases}

이 때, 나누는 구간 지점을 cutpoints 또는 knots라고 한다.

위 경우의 degrees of freedom (dof, 추정해야 할 parameter 수)은 8이다.

Knots에서 polynomial이 서로 연결되어 있으면, 이를 continous piecewise polynomial이라고 한다.

Splines

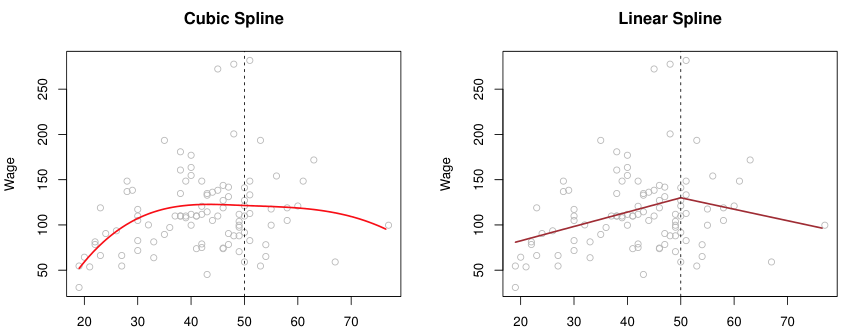
Spline이란, continous piecewise polynomial의 continuity를 최대로 만든 것을 말한다. Degree- $d$ spline은 각 knot에서 $d-1$ -th derivative가 존재해야 한다.

Linear Splines

구간 별로 linear regression을 적용한다.

K개의 knots가 있을 때, 각 knot에서의 continuity 제약에 의해 첫번째 구간을 제외한 나머지 구간은 1개의 parameter만을 추청하면 된다. 따라서, dof는 K+2가 된다.

y_i = \beta_0 + \beta_1 b_1(x_i) + \beta_2 b_2(x_i) + \cdots + \beta_{K+1} b_{K+1}(x_i) + \varepsilon_i

b_1(x_i) = x_i, \quad b_{k+1}(x_i) = (x_i - \xi_k)_+, \quad k = 1, \ldots, K

여기서 $\xi$ 는 knot을 의미한다.

Cubic Splines

각 knots에서 2nd derivative가 존재하는 continous piecewise cubic을 말한다.

dof는 첫번째 구간에서 4, 나머지 구간에서 1 씩 총 K+4가 된다.

y_i = \beta_0 + \beta_1 b_1(x_i) + \beta_2 b_2(x_i) + \cdots + \beta_{K+3} b_{K+3}(x_i) + \varepsilon_i

b_1(x_i) = x_i, \ b_2(x_i) = x_i^2, \ b_3(x_i) = x_i^3, \ b_{k+1}(x_i) = (x_i - \xi_k)_+^3, \quad k = 1, \ldots, K

Natural Cubic Splines

Cubic spline은 polynomial regression이 갖는 낮은 extrapolation 성능 문제를 여전히 가지고 있다. 이러한 문제를 완화하고자, K개의 knots가 있을 때, 첫번째와 마지막 구간의 경우 linear spline을, 사이 구간들은 cubic spline을 적용하는 방법을 생각해 볼 수 있다. 이를 natural cubic spline이라고 한다.

Natural cubic spline은 기존 cubic spline에서 2개의 구간이 linear하게 바뀌었으므로, dof = K가 된다.

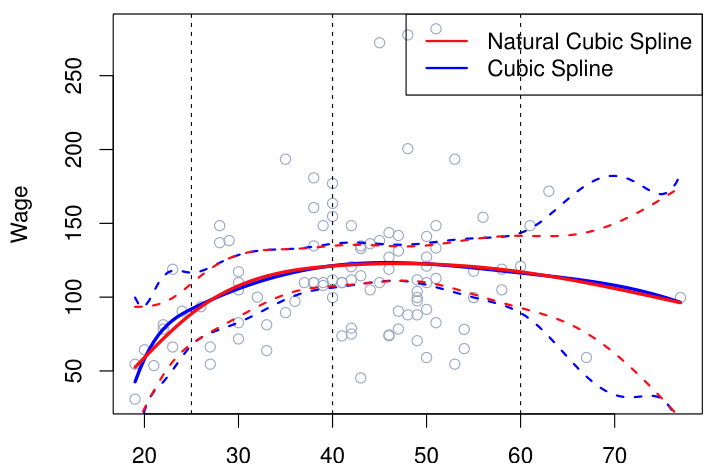
아래 그림은 degree-14 polynomial과 natural cubic spline(둘 다 dof=15)를 나타낸다. 동일한 dof를 갖지만 natural cubic spline이 더 안정적인 형태를 가지는 것을 볼 수 있다.

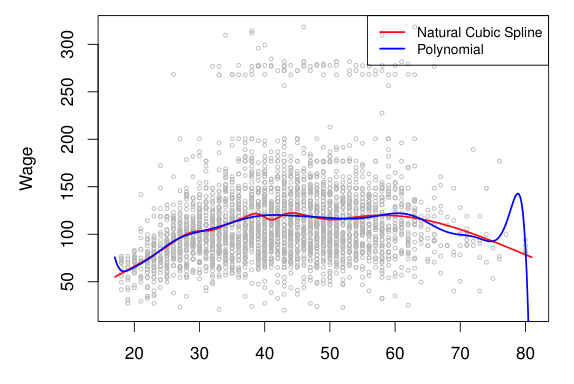
Knot Placement

Spline은 구간을 구분짓는 knot을 어떻게 설정하는지가 중요한 의사결정 요소이다. 무수히 많은 knot은 model의 flexibility를 지나치게 키울 수 있으므로 주의해야 한다.

일반적으로 knot는 같은 간격으로 배치하며, knot의 개수는 cross-validation을 통해 결정한다.

data가 flexible한 부분에는 knot을 많이 설정하고, 상대적으로 stable한 부분에선 보다 적은수의 knot를 설정하는 것도 하나의 방법이다.

Smoothing Splines

앞서 언급한대로, spline은 기본적으로 knot의 개수를 늘릴수록 flexibility가 증가하여 overfitting에 빠지기 쉽다. 이러한 관점에서 regularization이 적용된 optimization problem으로 spline을 최적화 하는 방법을 생각해 볼 수 있다.

Smoothing spline은 regularization이 추가된 spline regression으로, 아래 optimization problem의 solution이 되는 smooth function $g(x)$ 을 말한다.

\text{minimize}_{g \in S} \sum_{i=1}^n (y_i - g(x_i))^2 + \lambda \int (g''(t))^2 dt

여기서 $\lambda \int (g''(t))^2 dt$ 는 regularization을 위한 penalty term이다. 즉, $\lambda$ 로 smoothing spline의 flexiblity를 결정한다 (클수록 linear).

2nd derivative 크기에 penalty를 준다는 것은 $g(x)$ 의 굴곡진 정도를 어느정도 제한한다는 것이다.

Local Regression

Local regression이란 특정 data point 근처의 다른 data point들로부터 해당 지점에서의 prediction을 수행하고, 이를 모든 data point 지점에 대해 수행하여 non-linear function을 만들어 내는 방법을 말한다.

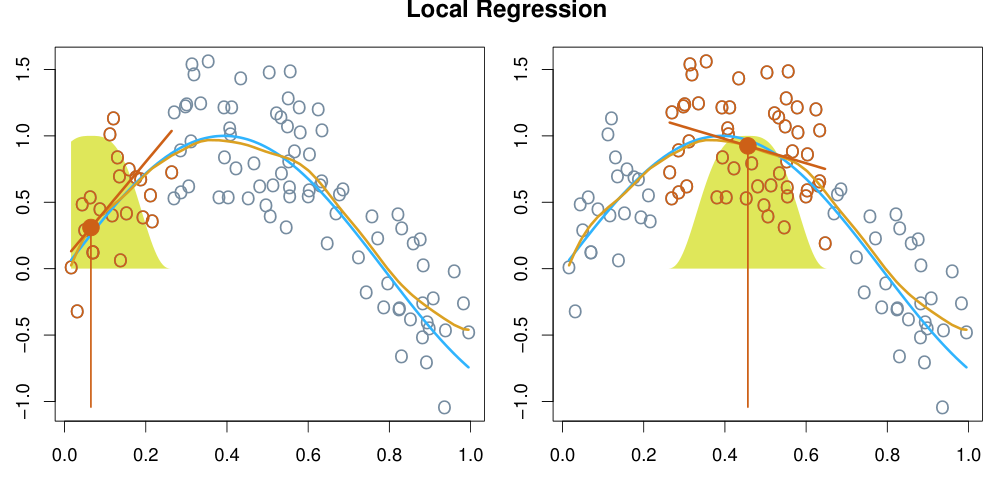
High-dimension data에 대한 local regression은 the curse of dimensionality에 의해 성능이 크게 떨어진다.

Generalized Additive Models

Generalized additive models (GAMs)은 여러개의 non-linear function들을 linear model처럼 연결하는 방법이다. 각 coefficient의 효과를 non-linear function으로 나타낼 수 있다. ( $\beta_j$ 는 각 $f_j$ 에 포함된다.)