Variational Inference

RECAP: Approximate Bayesian Method

Bayesian inference를 요약하면 다음과 같다.

• 데이터의 분포에 관한 모형 (likelihood, $L(\theta\mid X)$)와
• 모델을 정하는 모수 (parameter)의 사전분포 (prior distribution, $\pi(\theta)$)를 이용하여
• 모수의 사후확률 (posterior probability, $\pi(\theta\mid X)$)를 구하고,
• 이를 이용하여 모수에 관한 추론을 진행

이 때, likelihood가 복잡하거나, 데이터가 아주 큰 경우에는 사후확률을 계산하는 것이 쉽지 않다.

이에 따라, 여러 근사 베이지안 방법 (approximate Bayesian method)들이 제안되었다.

• 참고: Markov Chain Monte-Carlo (MCMC)

Variational Inference

Variational inference (변분 추론)은 또다른 근사 베이지안 방법의 일종이다. 이는 사후분포에 가까우면서 sampling이 상대적으로 쉬운 분포를 찾아, 이를 이용해 추론을 진행하는 것이다. 일반적으로 사후분포의 후보가 되는 분포에 대한 class를 정해두고, 이 가운데서 분포를 정하게 된다.

일반적으로 variational inference가 MCMC보다 속도가 빠르다.

꼭 Bayesian 방법이 아니더라도, MCMC는 분포로부터 표본을 sampling하는 기법으로, variational inference는 분포를 근사시키는 기법으로 사용되고 있다.

Variational inference의 과정을 설명하기 위해 다음을 가정하자.

• 데이터: $\mathbf{X} = (X_1, \cdots, X_n)$
• 은닉변수(잠재변수): $\mathbf{Z} = (Z_1, \cdots, Z_m)$
• 추가 모수: $\alpha$
• 목적: 사후분포 $p(\mathbf{Z} \mid \mathbf{X}, \alpha)$와 가까우면서 다루기 쉬운 분포(근사분포) $q(\mathbf{Z} \mid \nu)$를 찾아서 $\mathbf{Z}$를 생성하거나 사후분포의 특성값들을 근사적으로 구한다.

Finding the Approximate Distribution

우선 $p(\mathbf{Z} \mid \mathbf{X}, \alpha)$와 가까운 $q(\mathbf{Z} \mid \nu)$를 찾아내자. 이는 $q(\mathbf{Z} \mid \nu)$가 $p(\mathbf{Z} \mid \mathbf{X}, \alpha)$에 가장 가깝도록 하는 $\nu$를 찾는 문제로 볼 수 있다.

여기서 $\nu$는 variational parameter (변분 모수)라고 부른다.

그렇다면, 두 분포가 가깝다는 기준, 즉 분포 사이의 "가까움"을 나타내는 기준은 어떻게 정의할 수 있을까? 이에 대해서는 다양한 기준이 존재하지만, 가장 널리 쓰이는 기준으로는 Kullback–Leibler divergence, 또는 KL divergence가 있다.

KL Divergence

KL divergence는 정보이론 (information theory)에서 온 개념으로, 두 distribution의 가까움을 나타내는 값이다.

• If $q(\mathbf{Z}) = p(\mathbf{Z} \mid \mathbf{X})$, then $KL(q \parallel p) = 0$.
• $KL(q \parallel p) \geq 0$
• Asymmetric: $KL(q \parallel p) \neq KL(p \parallel q)$

KL divergence는 비대칭이므로 거리(distance)로 볼 수 없다.

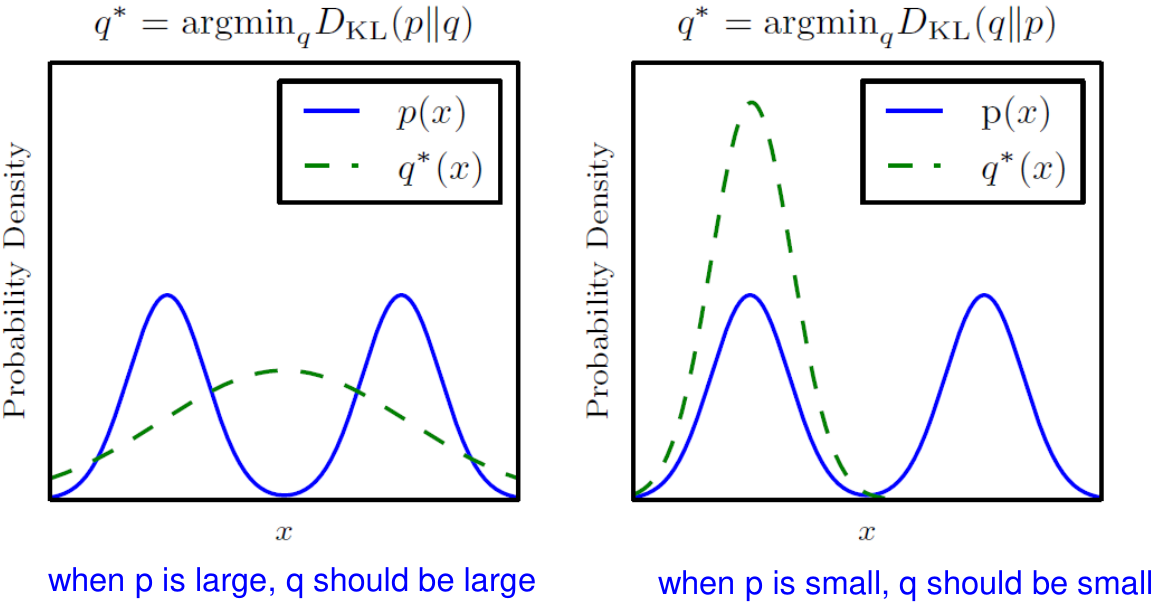
Minimize KL Divergence

다시, 원래의 근사분포를 찾는 문제로 돌아가자. KL divergence를 이용하면 해당 문제를 다음과 같이 표현할 수 있다.

$KL(q(\mathbf{Z}) \parallel p(\mathbf{Z} \mid \mathbf{X}))$을 직접 계산하기 위해서는 알지 못하는 분포 $p$에 대한 log 값에 대한 계산이 필요하다. 이에 대한 대체로 evidence lower bound (ELBO)라는 값을 이용한다.

Evidence Lower Bound (ELBO)

즉, evidence lower bound (ELBO)는 다음과 같이 정의된다.

이 때, $\log p(\mathbf{X})$는 $q$에 대해서 상수이므로 KL divergence 최소화 문제에 필요가 없다.

따라서, KL divergence 최소화 문제는 다음과 같이 쓸 수 있다.

$\log p(X)$는 관측값의 likelihood로 evidence라고도 불리며, ELBO는 이 evidence의 lower bound를 말한다.

ELBO는 다음과 같이 다시 쓸 수 있다.

마지막 식의 첫번째 항의 $\log p(\mathbf{X} \mid \mathbf{Z})$는 잠재변수 $\mathbf{Z}$가 주어졌을 때의 관측값 $\mathbf{X}$의 확률 (log scale)로, $\mathbf{Z}$의 log-likelihood로 볼 수 있다. 따라서, 첫번째 항은 $\mathbf{Z}$의 log-likelihood의 기대값이 된다. 따라서, ELBO를 최대화 하는 것은 $p(\mathbf{X} \mid \mathbf{Z})$를 크게 하도록 하는 것과 같고, 이는 likelihood를 증가시키는 또는 데이터를 더 잘 설명하는 $q(\mathbf{Z})$를 찾으려 하는 것과 같다고 볼 수 있다.

마지막 식의 두번째 항은 $\mathbf{Z}$의 사전분포 $p(\mathbf{Z})$와 $q(\mathbf{Z})$ 사이의 KL divergence이다. 따라서, ELBO를 최대화 하는 것은 사전분포 $p(\mathbf{Z})$와 가까운 $q(\mathbf{Z})$를 찾으려 하는 것으로 볼 수 있다.

즉, ELBO($q$)를 최대화 하는 것은 likelihood와 prior 사이에서 적절한 $q$를 찾는 것을 말한다.

Variational Familiy

위 문제에서 $q$를 찾는 것은, $Q$를 어떤 분포 집합 (probability distribution family)으로 놓느냐에 따라 계산 복잡도가 달라진다. 주로 많이 사용되는 가정은 mean-field variational family로, 이는 잠재변수가 서로 독립이면서 각기 다른 변분인자 (variational factor)에 의존하는 분포 집합을 말한다. 즉, $q(\mathbf{Z}) = \prod_{j=1}^m q_j(Z_j)$. 따라서, ELBO($q$)를 찾는 $\{ q_j^\ast \}$를 찾는 문제가 된다.

이러한 variational family는 $\mathbf{X}$에 의존하지 않는다.

Mean-field variational family보다 복잡한 family를 고려할 수도 있으나 일반적으로 계산상의 복잡도가 커진다. 구체적으로 어떤 variational family를 고려할지는 문제에 따라 다르며, variational family가 정해지면 최대화 시키는 최적화 알고리즘을 상황에 맞게 적용한다.

주어진 데이터 $\mathbf{X}$와, variational family $Q$가 정해져서 $\{ q_j^\ast \}$를 찾으면 필요에 따라 이를 이용하여 $Z_i$를 생성할수 있다. 이렇게 생성된 $\{Z_i\}$를 이용하여 데이터 $\mathbf{X}$와 유사한 $\mathbf{X^\ast}$를 생성할 수도 있다 (generative model).