[Python] MST 알고리즘

gramm·2021년 10월 13일

python 알고리즘

코딩 테스트 대비

목록 보기

5/6

선행 지식

그래프 자료구조
트리 자료구조

최소 신장 트리 (MST)

신장 트리 (Spanning Tree)

그래프 내의 모든 정점을 포함하는 트리

트리의 일종이므로, 사이클이 존재하지 않는다.
그래프의 정점이 n개라면, n - 1개의 간선을 가진다.

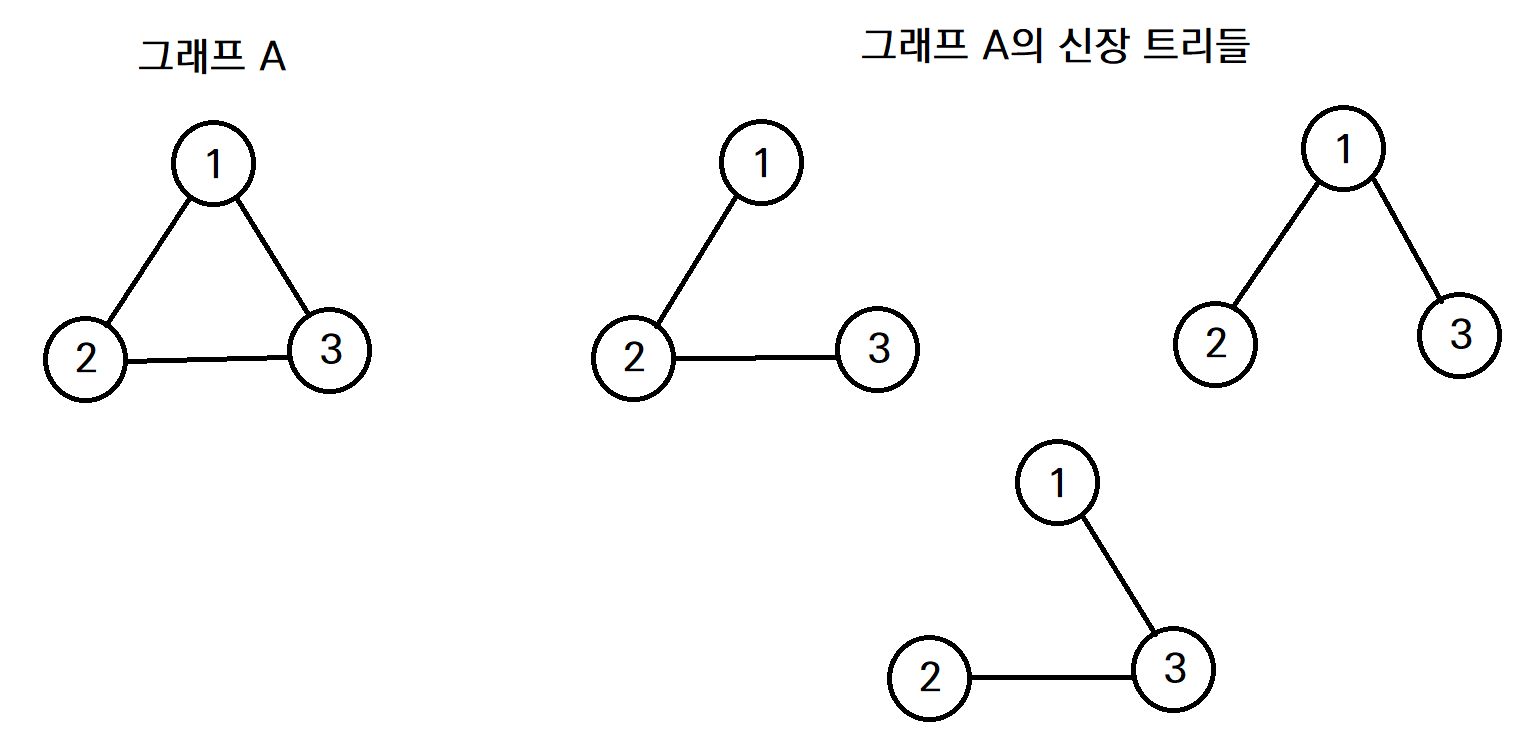
최소 신장 트리 (Minimum Spanning Tree)

무방향 그래프에서 간선들의 가중치 합이 최소인 신장 트리

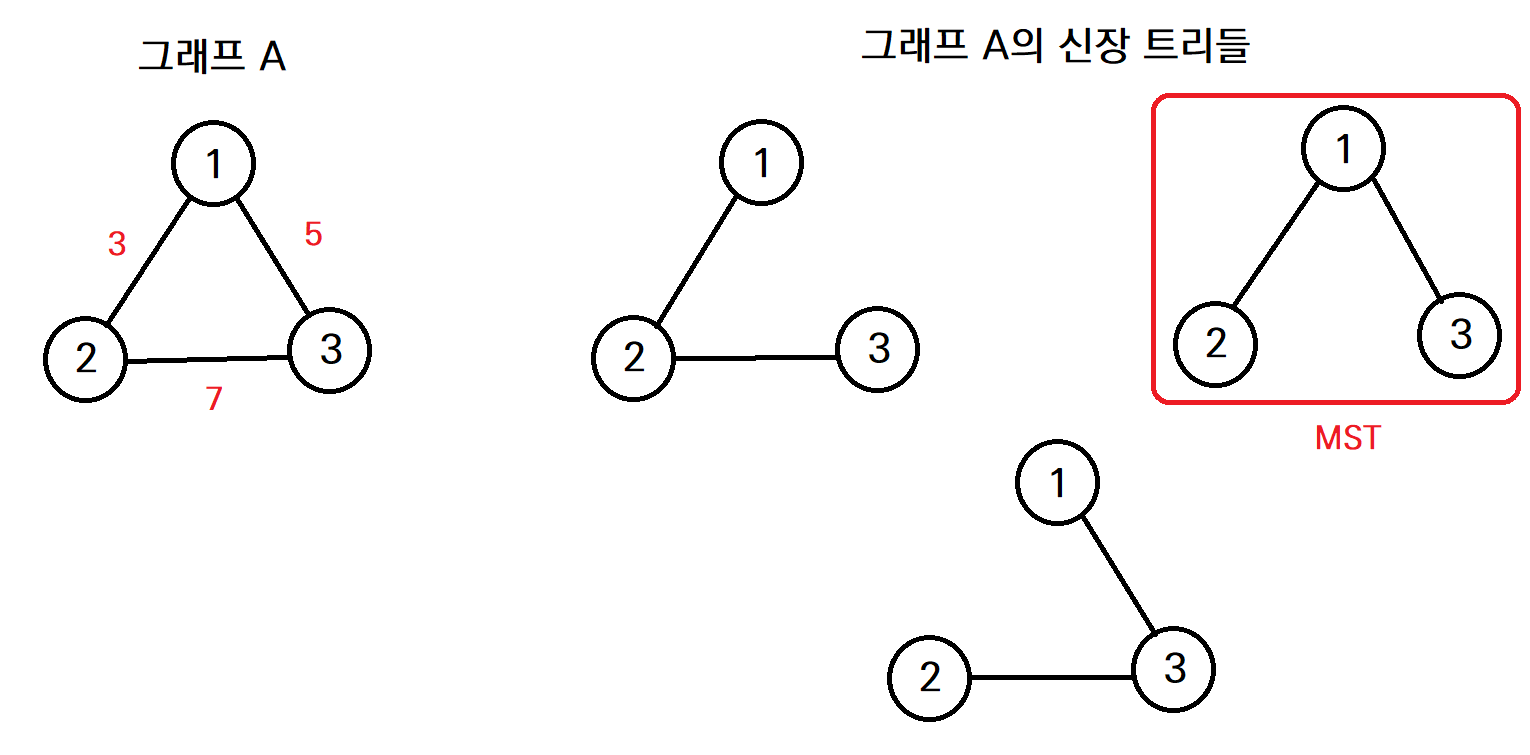
아래 그림에서, 3개의 신장 트리 중 오른쪽 신장 트리의 가중치 합이 8로 가장 적으므로, 해당 신장 트리가 그래프 A의 최소 신장 트리가 된다.

cf) 위키피디아에 따르면, 방향 그래프에서의 최소 신장 트리 문제는 Arborescence 문제라 불리며, Chu-Liu/Edmonds 알고리즘을 사용하여 풀 수 있다고 한다. (Chu-Liu/Edmonds 알고리즘)
최소 신장 트리를 구현하는 알고리즘으로는 Prim 알고리즘, Kruskal 알고리즘이 대표적이다.

Prim 알고리즘

시작 정점에서 출발하여 정점을 하나씩 선택하며 신장트리 집합을 확장해나가는 방법

그리디 알고리즘의 일종이다.

작동 순서

임의의 시작 정점을 하나 정한다. 시작 정점만 포함된 신장 트리 집합을 만든다.
N개의 정점이 모두 선택될 때까지
- 신장 트리 집합에 포함된 정점에 인접했으며 아직 방문하지 않은 정점 중, 최소 비용의 간선이 존재하는 정점을 선택한다.
- 선택한 정점은 신장 트리 집합에 포함시킨다.

인접 행렬을 이용한 코드 (직접 구현)

from math import inf


def prim(start):
    global N, adj_mat
    # visited_set: 현재까지 방문한 정점들의 집합
    visited_set = set()
    visited_set.add(start)
    distance = 0

    # N - 1개의 간선을 선택할 때까지 반복한다.
    for _ in range(N - 1):
        # min_dist: 현재 방문한 정점에서 갈 수 있는 간선의 최단 거리
        # next_node: 현재 방문한 정점에서 최단 거리로 갈 수 있는 정점
        min_dist, next_node = inf, -1

        # 현재까지 방문한 모든 정점에 대하여
        for node in visited_set:
            # 해당 정점과 연결되어 있고 아직 방문하지 않은 모든 정점 중
            # 소요 비용이 가장 작은 정점을 찾는다.
            for j in range(1, N + 1):
                if j not in visited_set and 0 < adj_mat[node][j] < min_dist:
                    min_dist = adj_mat[node][j]
                    next_node = j

        distance += min_dist
        visited_set.add(next_node)

    return distance


"""
N: 정점의 개수 (1번 ~ N번)
M: 간선의 개수
adj_mat: 그래프의 인접 행렬
"""
N, M = map(int, input().split())
adj_mat = [[0] * (N + 1) for _ in range(N + 1)]

for _ in range(M):
    # x와 y 사이의 가중치 = value
    x, y, value = map(int, input().split())
    adj_mat[x][y] = value
    adj_mat[y][x] = value

# 1번 정점에서 탐색을 시작
print(prim(1))

우선순위 큐를 사용한 코드 (링크)

코드는 아래 출처에서 확인할 수 있다.

[알고리즘] 프림 알고리즘(Prim Algorithm)

Kruskal 알고리즘

비용에 따라 정렬된 간선을 하나씩 선택하며 MST를 찾는 방법

프림 알고리즘과 마찬가지로, 그리디 알고리즘의 일종이다.

작동 순서

그래프의 간선들을 가중치를 기준으로 오름차순 정렬한다.
N - 1개의 간선이 선택될 때까지
- 가중치가 낮은 간선부터 탐색하면서, 사이클을 형성하지 않으면 간선을 선택한다.
- 사이클 형성 여부는 union-find 자료구조를 활용하여 판단한다.

union-find

서로소 집합을 표현하는 자료구조

서로소 집합은 중복된 원소가 없는 집합을 뜻한다.
집합에 속한 하나의 대표 원소를 통해 집합들을 구분한다.
find
- 원소가 속한 집합을 반환한다. (일반적으로 집합의 대표 원소를 반환)
- 여러 원소끼리 대표 원소를 비교하여, 같은 집합에 속했는지의 여부를 판단할 수 있다.

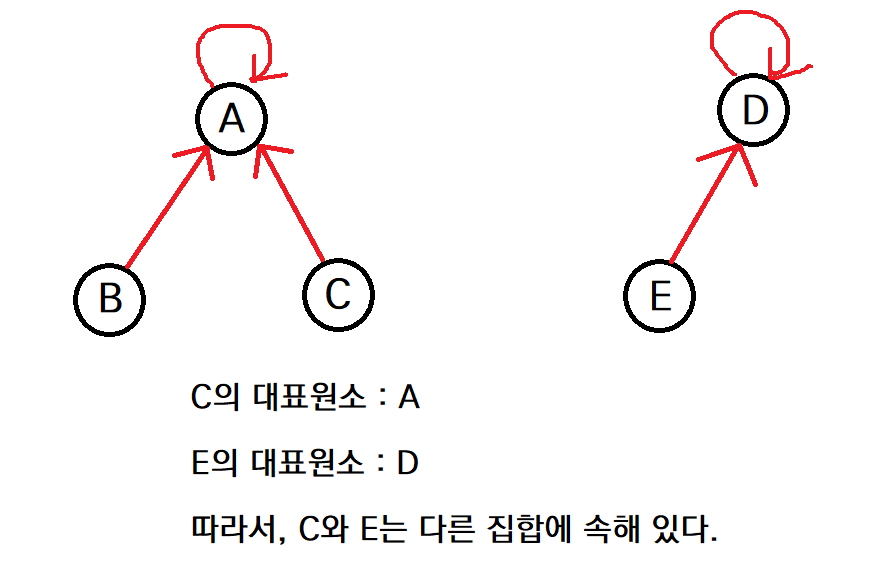
union
- 두 개의 집합을 하나의 집합으로 합친다.
- 한 집합의 대표 원소가 다른 집합의 대표 원소를 가리키게 하는 방식으로 구현한다.

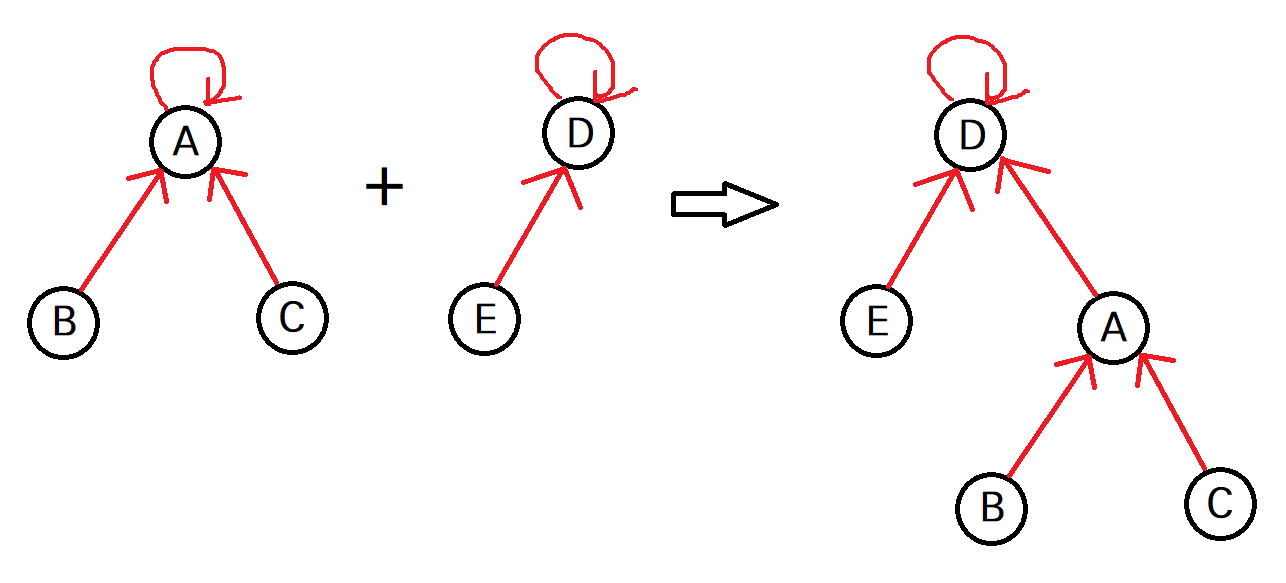
# 합치기 전
parents = [0, 0, 0, 3, 3]  # A, A, A, D, D

# 합친 후
parents = [3, 0, 0, 3, 3]  # D, A, A, D, D

예시 코드 (직접 구현)

def find_set(x):
    # x의 대표원소를 찾아서 리턴한다.
    while x != parents[x]:
        x = parents[x]
    return x


"""
N: 정점의 개수 (0번 ~ N-1번)
M: 간선의 개수
edges: 그래프의 간선 정보
"""
N, M = map(int, input().split())
edges = []

for _ in range(M):
    a, b, value = map(int, input().split())
    edges.append((a, b, value))

# 간선을 비용순으로 오름차순 정렬
edges.sort(key=lambda x: x[2])

# parents : 각 정점의 부모 원소 (초기 설정: 모두 자기 자신)
# cnt : 찾은 간선의 개수
parents = [x for x in range(N)]
distance, cnt = 0, 0

for a, b, value in edges:
    # 해당 간선이 사이클을 만들지 않는다면
    if find_set(a) != find_set(b):
        # union 연산을 수행한다. (b의 대표 원소가 a의 대표 원소를 가리키게 한다.)
        parents[find_set(b)] = find_set(a)
        distance += value
        cnt += 1

        # N - 1개의 간선을 모두 찾은 경우, 탐색을 종료한다.
        if cnt >= N - 1:
            break

print(distance)