최적화 문제
특정 조건을 만족하는 변수의 최대값 혹은 최소값을 찾는 문제
-
실제로 최적화 문제의 개념은 이보다 훨씬 복잡하다.
-
하지만 파라메트릭 서치를 이해하기 위해서는 위의 정의 이해해도 충분할 것이다.
-
ex. 모두에게 같은 개수의 구슬을 나누어줄 때, 가능한 구슬의 개수의 최대값은?
결정 문제
계산 문제 중 그 결과를 'Yes' 혹은 'No'로 답할 수 있는 문제
-
ex. 101은 소수인가?
-
ex. 그래프의 노드 A에서 노드 B로 가는 경로가 존재하는가?
파라메트릭 서치
최적화 문제를 결정 문제로 바꾸어 푸는 기법
파라메트릭 서치를 적용할 수 있는 문제
-
1 또는 0을 값으로 가지는 함수
f(i)가 있고, -
f(i) = 0이면 i보다 작은 모든 j에서f(j) = 0일 때 -
f(i) = 1인 i의 최소값 /f(i) = 0인 i의 최대값을 구한다.
최적화 문제 => 결정 문제
f(i) = 1이 되는 i의 최소값을 구하여라=>f(i) = 1인가?
위의 수학적 설명은 잘 와닿지 않지만, 사실 이해하면 어렵지 않은 내용이다. 예시를 통해 이해해보자. 친구의 생일 선물을 사려는 A는 자신이 살 수 있는 가장 비싼 선물을 사고자 한다. 이를 위해, 우선 쇼핑몰에서 파는 물건들을 가격순으로 정렬한다.
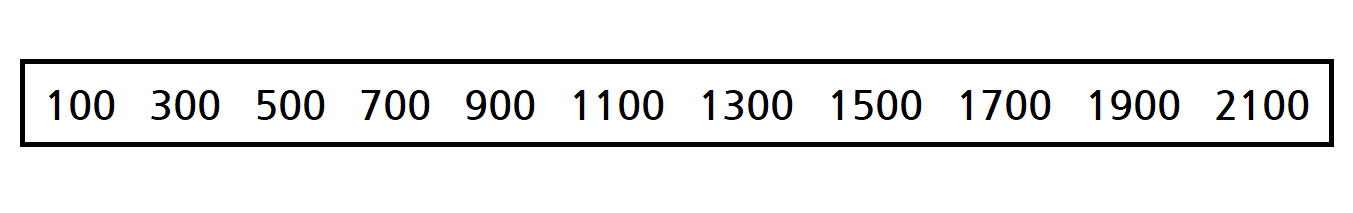
그리고 이분 탐색 알고리즘을 활용하여 살 수 있는 가장 비싼 선물의 가격을 탐색한다.
양쪽 끝을 각각 left, right로 둔 뒤, 매번 left와 right의 가운데를 mid로 두고, mid에 있는 물건의 가격을 지불 가능한 가격과 비교한다.
아래는 A가 낼 수 있는 가격이 1600원일 때, A가 살 수 있는 가장 비싼 선물을 찾는 과정이다.

위 이미지를 보면 이분 탐색과 약간 다른 점이 있다.
-
만약 가격이 1600원인 물건을 찾는 이분 탐색이었다면, 첫 줄에서
1100 < 1600이므로 left는 1100의 다음 인덱스로 두고 탐색을 이어갔을 것이다. 1100원짜리 물건은 찾는 물건일 수 없기 때문이다. -
반면 위에서는 left를 mid 자리에 두고 탐색을 이어갔다. 이는 1100원짜리 물건이 여전히 찾고자 하는 물건, 즉 살 수 있는 가장 비싼 물건일 수 있기 때문이다. 그리고 이는 곧 이분 탐색과 파라메트릭 서치의 차이를 보여준다. 이분 탐색이 특정 값 자체를 찾는 것이라면, 파라메트릭 서치는 특정 조건을 만족하는 최적의 (최소 or 최대의) 값을 찾는 것이다.
-
이렇게 이분 탐색과 파라메트릭 서치에서 조건문을 다르게 처리하는 부분은 실수하기 쉬운 부분이므로 주의해서 보는 것이 좋다.
예시 문제 - 나무 자르기 (백준 2805번)
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구한다.
해결 방법 : left, right을 각각 0, 1000000000 (나무의 최대 높이)로 설정한 뒤, 파라메트릭 서치를 통해 나무의 길이가 M미터 이상이 되는 절단기 설정 높이의 최대값을 구한다.
from sys import stdin
def get_tree_length(cut_height):
"""
절단기의 높이를 cut_height로 설정했을 때 얻을 수 있는 나무의 총 길이를 구한다.
"""
global trees
return sum([(tree - cut_height) for tree in trees if tree > cut_height])
def get_max_height(target):
"""
target미터 이상의 나무를 가져가기 위해 절단기에 설정 가능한 높이의 최댓값을 구한다.
"""
global trees
start, end = 0, 1000000000
while start <= end:
mid = (start + end) // 2
if get_tree_length(mid) >= target:
start = mid + 1
else:
end = mid - 1
return end
N, M = map(int, stdin.readline().split())
trees = [int(x) for x in stdin.readline().split()]
print(get_max_height(M))