연결리스트
원소를 저장할 때 다음 원소가 있는 원소의 위치를 포함해서 저장하는 방식의 자료구조이다.
원소들은 여러곳에 흩어져 있다.
예를 들면 '안', '녕', '하', '세', '요' 5개를 순서대로 기억해야 하는데 모든 문자가 일렬로 붙어있지 않고 여러 군데 흩어져 있는 상황이다.
연결 리스트에서는 '안'이 '녕'을 기억하고 '녕'이 '하'를 기억하는 방식으로 처음 시작인 '안' 만 기억하고 있어도 '안', '녕', '하', '세', '요'를 순서대로 알아낼 수 있게 된다.
연결 리스트 특징
배열과 연결리스트를 비교하는 경우가 많기 때문에 배열의 특징과 연결 리스트의 특징 차이점을 비교해보자.
-
k번째 원소를 확인하거나 변경할 때는
O(k)만큼의 시간 복잡도가 필요하다.
연결리스트의 구조상 n번째 원소를 찾기 위해서는 연결 리스트의 시작부터 확인해야 하기 때문이다.
배열과 달리 원소들이 연속된 공간에 위치하고 있지 않기 때문이다. -
임의의 위치에 원소를 추가하거나 제거할 때는
O(1)이다.
연결리스트의 큰 장점이라고 볼 수 있다. 배열과는 달리 앞 또는 뒤의 요소를 한 칸씩 이동시키지 않아도 되기 때문이다. -
원소들이 메모리 상에 연속되어 있지 않기 때문에 Cache hit rate는 낮지만 할당은 다소 쉽다.
연결 리스트 종류
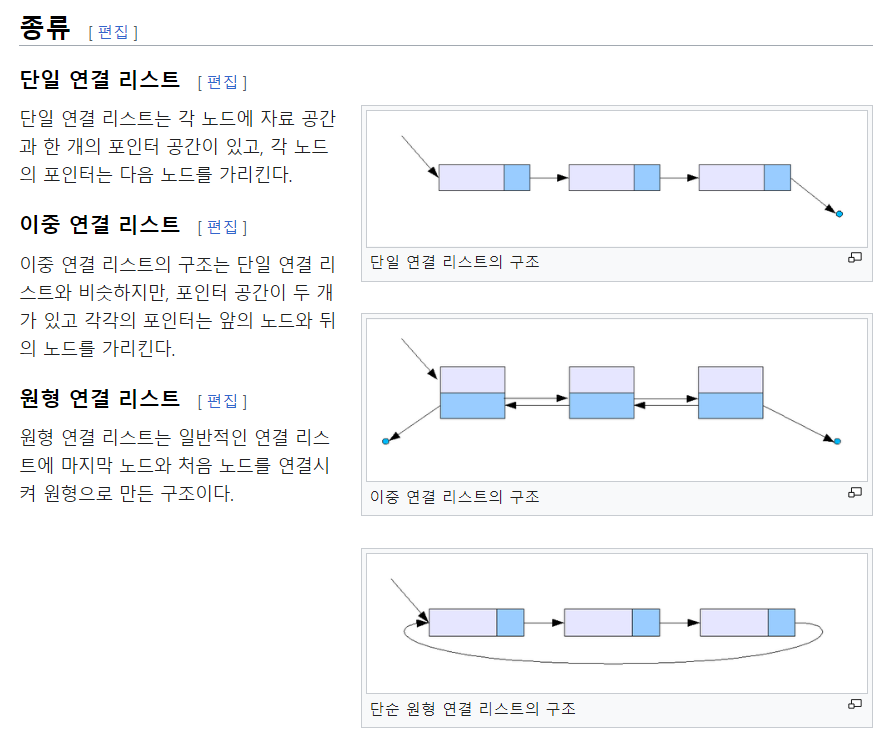
-
단일 연결 리스트(Singly Linked List)
각 원소가 자신의 다음 주소를 가지고 있는 연결 리스트이다. (다음 주소만 가지고 있기 때문에 이전 원소는 알 수 없다.) -
이중 연결 리스트(Doubly Linked List)
각 원소가 자신의 이전 원소와 다음 원소를 둘 다 가지고 있다. 원소가 가지고 있어야 하는 정보가 1개 더 추가되므로 단일 연결 리스트보다는 메모리가 더 추가된다는 특징이 있다. -
원형 연결 리스트(Circular Linked List)
원형 연결 리스트는 끝이 처음과 연결되어 있다.
각 원소가 단일 연결 일 수도 있고 이중 연결일 수도 있지만, 원소의 맨 마지막 원소가 첫번째 원소와 연결되어 있다는 특징이 있다.
배열과 연결 리스트 비교
| 배열 | 연결 리스트 | |
|---|---|---|
| k번째 원소 접근 | O(1) | O(k) |
| 임의 위치에 원소 추가/제거 | O(N) | O(1) |
| 메모리 상의 배치 | 연속 | 불연속 |
| 추가적으로 필요한 공간 (overhead) | - | O(N) |
참고 : 연결리스트에서 임의 위치에 원소를 추가/제거 할 때 일단 n번째 원소의 위치를 알아야 O(1)에 추가할 수 있다.
연결 리스트는 각 원소가 다음 원소나 이전, 다음 원소의 주소 값을 가지고 있어야 하므로 추가적으로 필요한 공간이 있어야 한다. (N에 비례하는 메모리를 추가로 소모)
배열과 연결 리스트는
선형 자료구조라고도 불린다.
연결 리스트 : 임의의 위치에 있는 원소를 확인/변경
연결 리스트에서 임의의 위치의 원소를 확인하거나 변경할 때는 O(N)의 시간 복잡도를 가진다.
왜냐하면, 해당 위치의 원소로 가기 위해서는 첫 번째부터 그 위치까지 순차적으로 찾아가야 하기 때문이다.
즉, 연결 리스트에서 우리는 첫번째 주소만 알고 있기 때문에 첫 번째 원소에서 N번째 원소로 찾아가기 까지 O(N)만큼 걸리는 것이다.
연결 리스트 : 임의의 위치에 원소를 추가
임의의 위치에 원소를 추가하는 연산은 O(1)이다.
왜냐하면, 예를 들어 1 뒤에 4를 추가하고 싶다고 가정했을 때 배열처럼 뒤의 원소를 모두 한 칸씩 이동시키는 작업이 필요하지 않기 때문이다. 연결 리스트에서는 원소의 주소만 변경을 해주면 되기 때문에 O(1)에 해결할 수 있다.
단, 추가하고 싶은 위치의 주소를 알고 있는 경우에만 O(1)이다. 주소를 모른다면 O(1)이 될 수 없다.
연결 리스트 : 임의 위치의 원소를 제거
추가와 마찬가지로 O(1)이다.
중간의 원소 하나를 지운다고 했을 때 배열처럼 한칸씩 이동시키는 작업 없이 다음/이전 원소의 주소값만 알려주면 되기 때문이다.
메모리 누수를 막기 위해 제거한 원소는 메모리에서 제거해주는 것이 좋다.
