[알고리즘] 추상자료형 ADT 개념과 종류

추상자료형(ADT)이란?

기능 구현 방법에 대해 명시하지 않고 순수한 데이터(자료)의 구조와 연산에 대한 명세이다.
구현 방법은 명시하지 않는다는 점에서 자료구조와 다르다.

✏️ 데이터 구조 기본 재료 : 배열 & 연결리스트

• 배열
  • 구성 : 베이스 + 오프셋
• 연결리스트
  • 구성 : 명(시작 위치) + 크기(노드 수)
  • 연결 리스트는 동적 메모리 할당
  • 열결 리스트 종류 : 단일, 이중, 원형 등

1. 리스트 ADT

• 연속적인 임의 개체
• 순위(rank)를 통해 접근, 삽입, 삭제
• 순서가 있는 집단을 저장하기 위한 기초적/일반적 구조
• 스텍, 큐, 집합, 소규모 데이터베이스 등 더 복잡한 데이터 구조 구축을 위한 재료로도 많이 사용
• 실행시간(Big Oh)

작업	배열	연결리스트
size, isEmpty	1	1
get	1	n
set	1	n
add, remove	n	n
addFirst, removeFirst	n	1
addLast, removeLast	1	1

2. 집합 ADT

• 중복 x, 순서 x
• 일반적으로 연결리스트로 구현(배열로도 가능은 함)
• 기억장소 사용 : $O(n)$

3. 스택 ADT

• First In Last Out 순서
• Top(최상위 요소 위치)에서 삽입, 삭제
• 배열, 연결리스트 둘 다 사용가능
  (일반적으로 연결리스트가 효율적인 다른 ADT들과 달리, 배열 이용도 good)
• 기억장소 사용 : $O(n)$
• 각 작업 실행시간 : $O(1)$

4. 큐 ADT

• First In First Out 순서
• 삽입은 뒤(rear), 삭제는 앞(front)에서 수행
• 배열에 기초한 큐
  • 배열을 원형으로 사용
  • f : front 위치. 빈 큐와 만원 큐를 차별하기 위해 항상 비워둠
  • r : rear 위치
• 연결리스트에 기초한 큐
  • f : 첫 번재 노드를 가리키는 포인터
  • r : 마지막 노드를 가리키는 포인터
  • 각 노드는 원소와 포인터로 구성
• 성능
  • 기억장소 사용 : O(n)
  • 실행시간 : O(1)

4-1. 우선 순위 큐 ADT

• 각 항목을 (키, 원소) 쌍으로 저장
• 삭제 시, removeMin()으로 최소 키를 가진 원소를 삭제하여 반환
• 무순리스트로 구현
  • 삽입 시간 : O(1)
  • 삭제 시간 : O(n) - 최소 키를 찾기 위해 전체 순회
• 순서 리스트로 구현
  • 삽입 시간 : O(n) - 삽입할 위치 찾기
  • 삭제 시간 : O(1) - 최소 키가 리스트 맨 앞에 있음
• 위 2가지 경우 모두, 배열과 연결리스트 무엇으로 구현하든 차이가 없다. (배열의 경우 move연산이 필요하다는 차이는 있다.)

5. 사전 ADT

• (키, 원소) 쌍의 모음

• 탐색

  • key와 연관된 데이터 원소를 반환하는 것
  • 사전을 구현하는 가장 큰 목적이다.

A. 무순사전 ADT

• 무순리스트로 구현된 사전
• 성능
  • 삽입 : O(1) - 맨 앞이나 맨 뒤에 삽입
  • 탐색, 삭제 : O(n) - 선형탐색(리스트 전체 순회, key 하나씩 다 검사)

B. 순서사전 ADT

• 순서리스트로 구현된 사전
• 성능
  • 삽입, 삭제 : O(n) - 최악의 경우 n개의 기존 항목 이동 필요
  • 탐색 : O(log n) - 이진탐색

---

6. 트리 ADT

• 계층적으로 데이터 저장
• 부모 원소와 자식 원소 구조
• 사이클이 없는 연결 그래프
• 경로 길이 : 경로 내 간선의 수
  • 깊이 : 루트->노드의 경로 길이
  • 높이 : 외부노드->노드의 경로길이 중 최대값
• 깊이 / 높이 구하기 성능
  • 실행시간 : O(n)
  • n은 트리 내 총 노드의 수
  • 깊이 : 루트부터 내려가며 depth+1을 재귀적 실행
  • 높이 : 자식 노드 중 가장 높은 높이+1을 재귀적 반환
• 순회
  • 선위순회, 중위순회, 후위순회
  • 부모노드를 방분하는 타이밍 기준
• 순서트리 : 각 노드의 자식들 사이에 선형 순서가 정의되어 있는 트리

A. 이진트리 ADT

• 각 내부노드가 2개의 자식을 갖는 순서 트리
  • 왼쪽, 오른쪽 순서
• 한쪽으로 너무 치우치지 않게 적정 이진 트리로 구현하기
• 외부 노드 수 : 내부 노드 수 + 1
• 이진 트리 높이 $h$ >= $log_2(n+1)-1$
• 배열에 기초한 이진트리
  • 왼쪽 자식의 위치 : 2i
  • 오른쪽 자식의 위치 : 2i+1
  • 부모 위치 : $\lfloor 2i \rfloor$
  • 적정 이진트리가 아닐 경우, 빈 공간이 많이 비효율적
• 연결이진트리
  • 각 노드는 4가지 요소로 구성된다.
  • 부모 포인터, 원소, 왼쪽 자식 포인터, 오른족 자식 포인터
• size, isEmpty, root, parent, children(v), leftChild, rightChild, sibling, isInternal, isExternal, isRoot, setElement, swapElements
  위 함수 모두 O(1)3

B. 힙 ADT

• 정의
  • key(v) >= key(parent(v)) 를 만족하는 완전이진트리
    • 위->아래, 왼쪽->오른쪽 순서로 빈곳 없이 채움
    • 부모 key < 자식 key
  • 내부노드에 키 저장(외부 노드는 null)

• 높이 : $O$ (log $n$)
  • 각 깊이 별 노드 수 : $2^h$
  • 모두 더하면 1+2+$2^2$+...+$2^h$
  • 트리의 전체 깊이가 h이면
    1+2+...+$2^{h-1}$+1 = $2^{h-1}$+1 <= n
  • h <= $log_2n$+1
• 우선순위 큐로 사용 가능하다.
  • 삽입 : 맨뒤에 삽입 후, upheap
  • 삭제 : 루트 키 삭제 후, 맨 뒤 값을 루트에 넣고, downheap
  • upheap
    • 부모 노드가 더 크면 swap
    • 부모 노드가 더 작거나 루트에 도달하면 종료
  • downheap
    • 두 자식 중 더 작은 노드와 swap
    • 두 자식노드가 모두 더 크거나 외부 노드 도달하면 종료
• 배열로 구현하는 것도 좋다.
  • 일반적으로 트리는 연결리스트로 구현한다.
  • 하지만 힙은 완전이진트리로서 중간에 빈 칸이 없기 때문에 배열로 구현하기에도 적합하다.
  • 배열로 구현하는 경우 외부노드는 표현하지 않는다.
  • 첨자 0은 사용하지 않고, 마지막 노드는 첨자 n으로 표시한다.
• 실행시간
  • size, isEmpty : O(1)
  • 삽입, 삭제 : O(log $n$)
  • 마지막 노드 갱신 : 배열 O(1), 연결리스트 O(log $n$)

C. 이진탐색트리

• 모든 subtree에서
  왼쪽부트리 속 노드의 key < 기준 노드의 key <= 오른쪽 부트리 속 노드의 key
• 중위순회 시, 키가 증가하는 순서로 방문하게 된다.

• 탐색 : 이진탐색
• 삽입 : 삽입할 키를 탐색해서, 해당 키가 없을 경우 외부노드에 도착하게 된다. 해당 외부 노드에 삽입하고 내부 노드로 확장한다.(해당 키가 이미 있을 경우 삽입하지 않는다. 중복은 허용하지 않기 때문이다.)
• 삭제
  • 자식 중 외부노드가 있는 경우 : 부모노드를 외부노드의 형제노드인 자식노드와 연결한다.
  • 자식이 모두 내부노드인 경우 : 삭제해야할 노드 자리에 중위순회 계승자를 이동시킨다.
    • 중위순회 계승자 : 삭제할 노드의 오른쪽 자식노드를 기준으로, 왼쪽 자식노드를 따라 계속 내려가면 나오는 노드
• 성능
  • 최악 : O(n) - 한쪽으로 계속 이어지는 트리
  • 최선 : O(log n)

D. AVL 트리

높이균형속성(좌우 높이 차이가 1이 넘지 않는) 이진탐색트리

• 삽입, 삭제 시 개조(회전)를 통해 높이 균형 속성을 회복한다.

  • 단일 회전, 이중 회전이 있다.
  • 둘 다, 3개의 중심 중 가운데를 중심으로 회전한다.
    가운데 : 3개를 중위순회하며 차례로 a, b, c라고 부를 때, b를 의미한다.
    

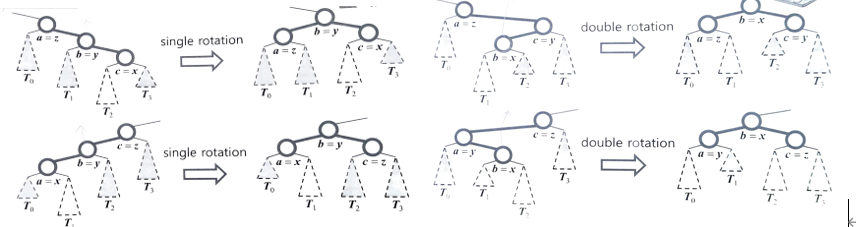
• 개조 기준

  • 삽입/삭제한 위치에서 루트로 올라가다가 처음 만나는 불균형노드를 z
  • z의 높은 자식을 y
  • y의 높은 자식을 x

• 삭제 시엔 개조 후에도 불균형이 있을 수 있다. 따라서 개조를 다시 호출해야 한다.

  • 방근 개조된 subtree의 루트에서, 전체 tree의 루트로 타고 올라가며, 불균형이 있을 시 개조 작업을 계속한다.

• 성능
  • 공간 사용량 : O(n)
  • 높이 : O(log n)
  • 3-노드 개조(한번의 재구성) : O(1)
  • 탐색 : O(log n)
  • 삽입/삭제 : O(log n) - 찾기 log n, 트리따라 올라가며 개조 log n

E. 스플레이 트리

• 트리의 노드가 접근되면, 그 후 스플레이 되는 자기조정 이진탐색트리
• 스플레이 : 노드가 접근되면, 노드를 연속적인 재구성으로 루트로 이동시킴
  • 탐색 : 발견된 내부노드 혹은 탐색 실패한 외부노드의 부모노드를 스플레이
  • 삽입 : 삽입한 내부노드를 스플레이
  • 삭제 : 삭제된 내부노드의 부모노드를 스플레이
• 성능
  • 탐색, 삽입, 삭제 시간 : O(log n) 상각 실행 시간
  • 각 항목에 대한 접근빈도가 균등하지 않은 사전에 사용하면 유리하다.

F. 최소신장트리(MST)

• 신장부그래프(모든 정점 포함하는 부그래프) 중 가중그래프의 총 간선 무게가 최소인 트리
• 속성
  • 사이클속성
    : 프래프G의 최소신장트리T가 있다. 이때 T에 포함되지 않지만 G에 포함되는 간선 e를 추가해서, 사이클C을 형성해보자. 이때 사이클 C의 e이외의 모든 간선의 가중치보다 e의 가중치가 크다.
  • 분할속성
    : 분할을 가로지르는 최소 무게 간선e를 포함하는 최소신장트리가 반드시 존재한다.

---

7. 그래프 ADT

간선 + 정점의 쌍

• 종류
  방향그래프, 무방향그래프

• 용어
  간선의 끝점, 정점의 부착간선, 정점의 인접정점
  차수 : 정점에 연결된 간선의 수
  병렬간선 : 양 끝점을 공유하는 간선
  루프 : 양끝점이 같은 간선
  경로 : 정점과 간선의 교대열
  단순경로 : 모든 정점과 간선이 유일한 경로
  싸이클 : 시작정점 == 끝 정점
  단순싸이클 : 모든 정점과 간선이 유일한 싸이클
  연결성 : 모든 정점쌍에 대해 경로가 존재
  연결요소 : 서로 연결되어 있는 부그래프
  밀집도 : 정점 대비 간선의 수

• 부그래프 subgraph
  정점과 간선이 모두 부분집합인 그래프

• 신장부그래프(spanning subgraph)
  : 정점은 모두 사용, 간선은 부분집합

  • 신장 트리 : 신장 부그래프 중 트리인 것

---

8. 해시테이블 ADT

• 키-주소 매핑에 의해 구현된 사전 ADT
  • Dictionary ADT와 유사 (엄밀하겐 구분할 때도 있지만, 구분 없이 사용되기도 한다)
• 버켓배열 + 해시함수 구조
  • 버켓배열
    • 버켓(슬롯) : 원소 쌍을 담는 그릇, 버켓 배열의 각 셀
  • 해시함수 : 주어진 key를 주소(고정된 범위의 인덱스)로 메핑하는 함수
    • 해시코드맵 : keys -> integers
      • 메모리 주소, 정수 캐스트(비트값 활용), 요소합, 다항누적 등
    • 압출맵 : integers -> [0, m-1]
      • 나누기, 승합제(선형+나누기)
• 성능
  • 탐색, 삽입, 삭제 시간복잡도
    • 최악의 경우 O(n)
    • 기대시간은 O(1) - 키들이 A[0, M-1] 범위의 유일한 정수인 경우
      • 종종 비현실적이라는 단점이 있다.
  • 공간복잡도 : n
    • M >> n 공간낭비로 비효율적일 수 있다.
• 좋은 해시함수 : 무작위하게 분산, 빠르고 쉬운 계산

• 충돌해결
  • 분리연쇄법 : 포인터
  • 개방주소법
    • 선형조사법 : 바로 다음 셀(1차 군집화 문제)
    • 2차 조사법 : $i^2$를 더하기
    • 이중해싱 : i*h(k)를 더하기
• 적재율 : 해시배열 크기대비 얼마나 저장되었나
  • 분리연쇄법 : a<=1 이 좋다.
  • 개방주소법 : 항상 a<=1이다. a<=0.5이면 좋다.
• 재해싱 : 적재율을 상수 이하로 유지. 배열 크기 증가 & 재배치