[MDP] Markov Decision Process (MDP) 의 개념

MDP 란?
- Markov Decision Process의 약자
- Sequential Decision Making under Uncertainty를 위한 기법
- 강화학습(Reinforcement Learning, RL)을 위한 기본 기법
- 알고리즘(transition probability, reward function)을 알고 있을 때는 MDP(stocasitc control 기법)을 이용한다.
- 알고리즘을 모르고 simulation 결과(reward 값)를 활용할 때는 강화학습을 이용한다.
MDP 구성요소 <S,A,P,R,γ>
- S : set of states(state space)
- state st∈S : the status of the system, environment
- discrete인 경우, S={1,2,...,n}, continuous인 경우, S=ℜn
- A : set of actions(action space)
- action at∈A : input to the system
- discrete인 경우, A={1,2,...,n}, continuous인 경우, A=ℜn
- the decision maker observes the system state and choose an action either randomly or deterministically
- p : state transition probability
- p(s′∣s,a):=Prob(st+1=s′∣st=s,at=a)
- 현재 state가 s, action은 a 일 때, 다음 state가 s'이 올 확률
- deterministc의 경우, 하나의 state(s')에 대해서만 1, 나머지는 0으로 한다.
- reward function rt
- rt=r(st,at) : 현재 상태 st에서 action at를 수행할 시의 결과
- 현재(t) step에 agent가 얼마나 잘 하고 있는가
- long term effect을 측정할 순 없다. 즉각적인 것만 방영한다.
- 장기적인 영향은 이후 이를 누적해서 판단한다.
- discount factor γ
- γ∈(0,1]
- 미래에 대한 discount 정도
- 0에 가까울 수록, 미래에 대한 가중치를 크게 감소시키는 것이고
- 1에 가까울 수록, 미래와 현재의 가중치를 거의 동일하게 주는 것이다.
그 외 주요 용어
- Decision Rule
- 각 state에서 어떤 action을 선택할지에 대한 규칙
- 분류 1 : 사용하는 information 범위
- Markov : 현재 state에만 의존
- history dependent : 현 step까지 방문한 모든 state에 의존
- 분류 2 : implementation 방법
- deterministic : state 하나 입력 시, action 하나 나옴
- stochastic(randomized) : state 하나 입력 시, A 확률 분포 나옴(해당 확률에 따라 random으로 action 선택)
- 일반적으로 Deterministc Markov decision rule을 가장 선호한다.
- history보단 Markow이, stochastic보단 deterministic이
상대적으로 훨씬 간단하여 효율적이기 때문이다.
- 이 다음으로는 Randomized Markov가 선호된다.
- 표기 : πt:S→A (Markov Deterministic decision rule)
- Deterministic Markov : πt(s)=a
- Randomized Markov : πt(⋅∣s) 확률 분포
- e.g. πt(a1∣s1)=0.3,πt(a2∣s1)=0.7
- 확률 값으로 나타난다.
- s가 같을 경우, 그 합은 1이 되어야한다.
- Deterministic History : πt(s0,a0,s1,a1,…,st)=a
- Randomized History : πt(⋅∣s0,a0,s1,a1,…,st) 확률 분포
- policy
- mapping from state to action
- 모든 state에 대한 decision rule을 모아둔 것
- π:=(π1,π2,…)
- in Deterministic case, π(st)=at
- in Stochastic(randomized) case, π(a∣s)=Prob(at=a∣st=s)
- stationary : t에서 decision rule이 같음
- 이때 optimal 인 경우가 많다.
- 이땐 decision rule과 policy를 구분하지 않는다.(일반적으로 policy 사용)
- value function vπ(s)
- 현재 state st에서 출발해서, 앞으로 얻을 수 있는 누적 reward
- vπ(s):=Eπ[∑γ=t∞γτ−tr(sτ,aτ)∣st=s]
- t which used in st,at, etc.
MDP 의 목표
- 누적 reward를 최대화하는 optimal policy를 찾는다.
π∈ΠmaxEπ[t=0∑∞γtr(st,at)]
- value function으로 정의하면 아래와 같다.
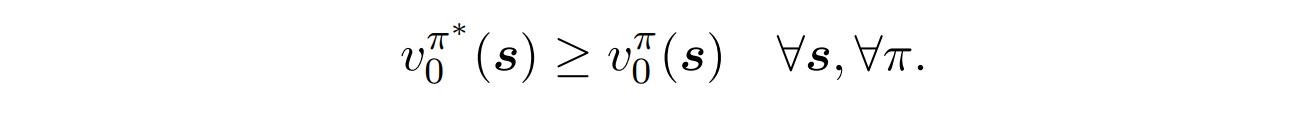
- st에서 action 선택 시 long term effect를 고려해야한다.
- 장기적 이득을 위해 현재를 희상할 수 있다.
- action에 따라 다음 state이 달라지는 것을 고려한다.
사용 방법
- policy 최적화의 어려움
- policy는 규칙/함수이므로, MDP는 함수최적화문제이다.
- 따라서 무한 차원 문제로 풀기가 어렵다.
- 직접적인 gradient descent나 optimization 알고리즘을 적용할 수 없기 때문이다.
- DP(Dynamic Programming) 사용
- 하나의 문제를 여러 개의 쉬운 문제로 나누어 푼 후, solution을 모아 푸는 것
- sequential Decision Making에 특화된 알고리즘
- value function과 Bellman Equation을 이용한다.(다음 포스트 참고)

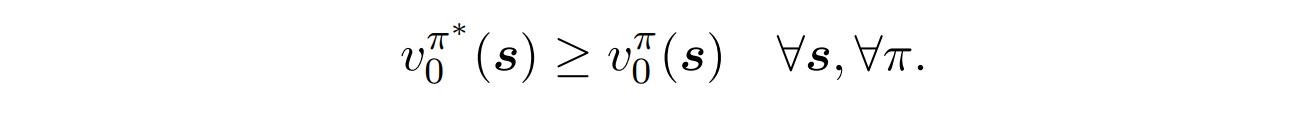

중간중간 책 사진이 있던데 무슨 책인지 알 수 잇을 가요?