- MDP의 목표는 누적 reward를 최대화하는 optimal policy를 찾는 것이다.(Policy Evaluation)
- optimal policy를 찾는 것은 함수 최적화 문제이다. 따라서 Gradient Descent나 일반적인 최적화 알고지름으로 풀기 어렵다.
- 따라서 상대적으로 쉬운 문제인 optimal value function 구하기를 반복하는 방식을 대신 사용한다.(Dynamic Programming)
- 이때 필요한 식이 Bellman Equation이다.
Optimal Value Function
-
value function은 현 state s 이후로 얻을 수 있는 누적 reward를 의미한다. (이전 포스트 참고)
-
optimal value function 는 모든 가능한 policy case에서 최대의 value function을 의미한다.
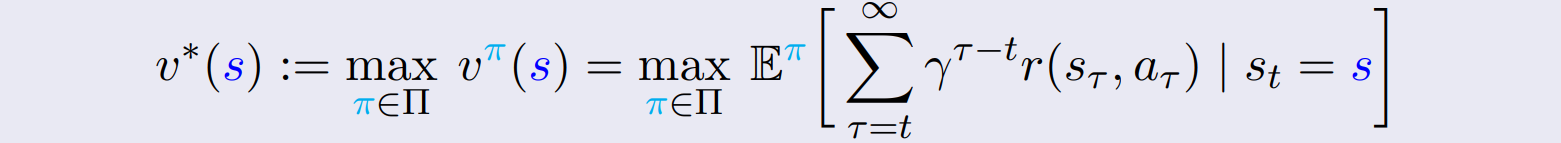
-
optimal policy를 통해 구하는 value function은 optimal value function과 일치한다.
- 드물게 optimal policy의 존재가 보장되지 않는 경우가 있다. 이 경우 아래와 같이 -optimal policy를 정의해 사용한다. (for an )
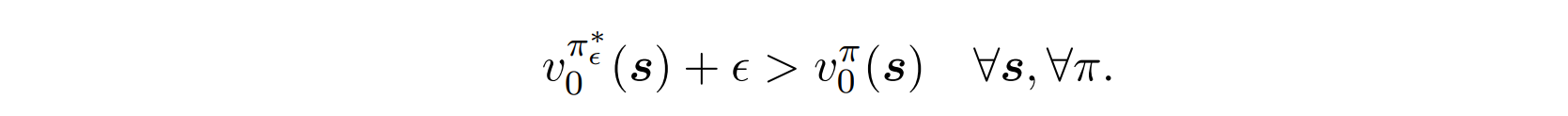
- 증명(finite-horizon deterministic MDPs의 경우)

- 드물게 optimal policy의 존재가 보장되지 않는 경우가 있다. 이 경우 아래와 같이 -optimal policy를 정의해 사용한다. (for an )
-
따라서 를 찾으면 optimal police를 찾을 수 있다.(MDP 문제를 풀 수 있다.)
이를 아래에 나올 Bellman Equation으로 표현하면 아래와 같다.
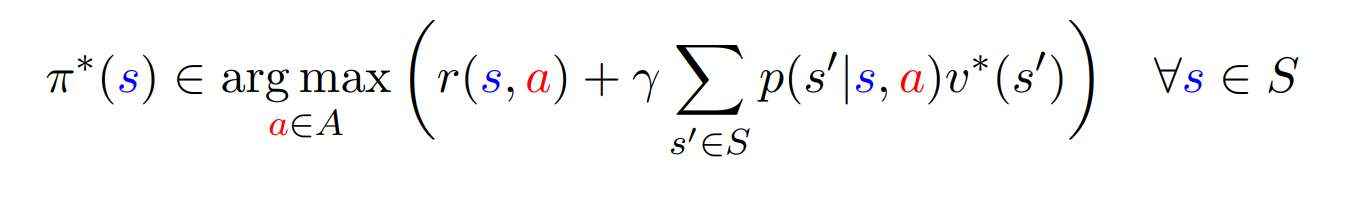
Bellman Equation

- optimal value function은 위와 같은 Bellman Equation의 unique solution이다.
식 구하기
- 를 나누기
- value function을 immediate reward + value of next state로 나눈다.
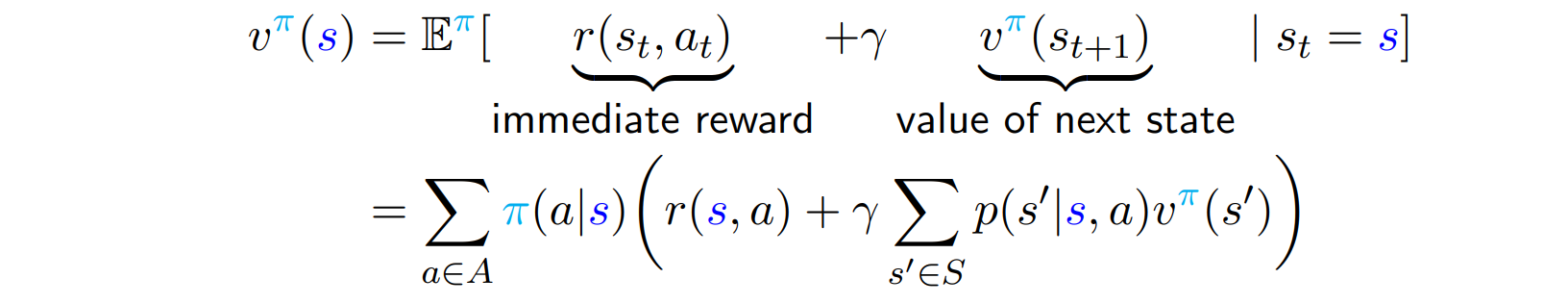
- 위 식을 matrix form으로 나타낼 수 있다.
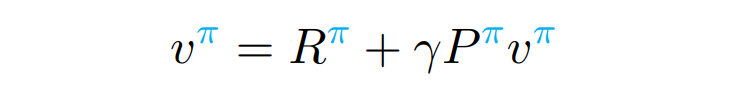
- 위 식을 operator form으로 나타낼 수 있다.
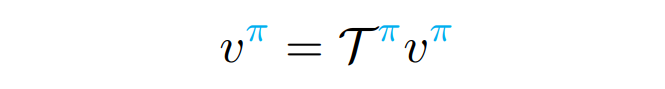
- 위 식을 matrix form으로 나타낼 수 있다.
- max 적용
optimal value function의 조건대로 위 식에 max를 취한다. - policy 대신 a를 maximize한다.
- 문제가 훨씬 쉬워지는 대신, 여러 개로 쪼개진다.(Dynamic Programming)
- operator form으로 아래와 같이 나타낼 수 있다.
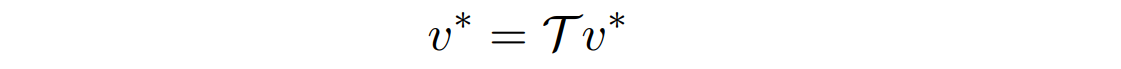
증명하기(Finite-Horizon MDPs 경우)
- Bellman Equation의 unique solution이 Optimal Value Function임을 증명한다.
- <= 증명
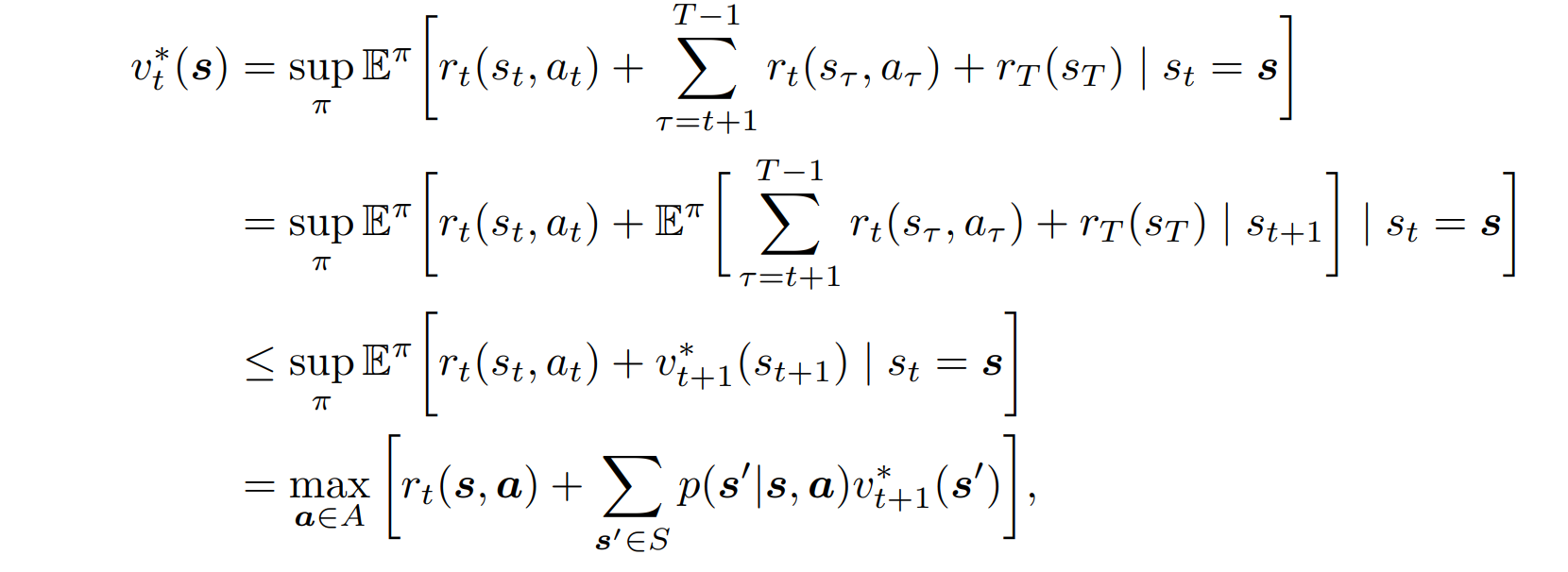
- 증명

