구성요소

- 종류는 기본 MDP 구성요소에서 설명한 것과 동일
- reward와 transition probability는 시간에 따라 변하지 않는다(stationary)
- finite에선 각각 지정 가능하지만, infinite에선 너무 난해 혹은 불가능하다.
- A와 S는 finite이고, 따라서 reward는 bounded
- 아래를 만족하는 상수 M이 존재한다.
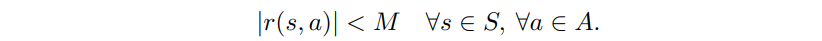
- 아래를 만족하는 상수 M이 존재한다.
Value Function
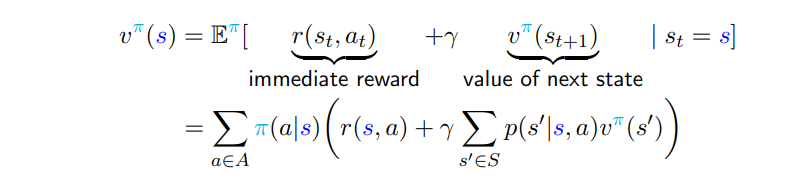
증명
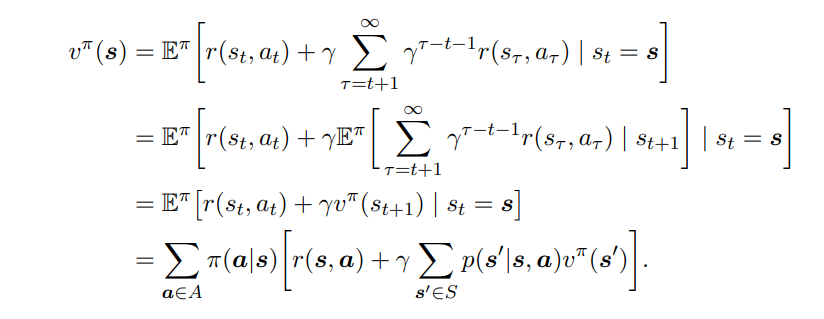
Vector Form

- 의 eigenvalues <= 1
eigenvalue는 matrix의 사이즈가 얼마나 바뀌는가를 나타내는 값이다.
P는 transition probability로 질량이 추가되거나 하지 않는다. - unique solution을 갖는다.
- 이므로 의 eigenvalue 는 0이 아니다. 따라서 inverse를 갖는다.
- 따라서 아래와 같은 linear solution으로 나타낼 수 있다.
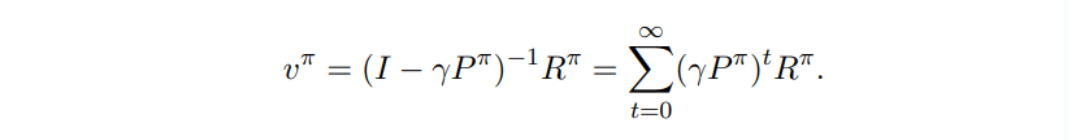
- large scale problem 용으로는 inverse 계산이 비효율적이다.
Operator Form
- operator 를 아래와 같이 정의한다.
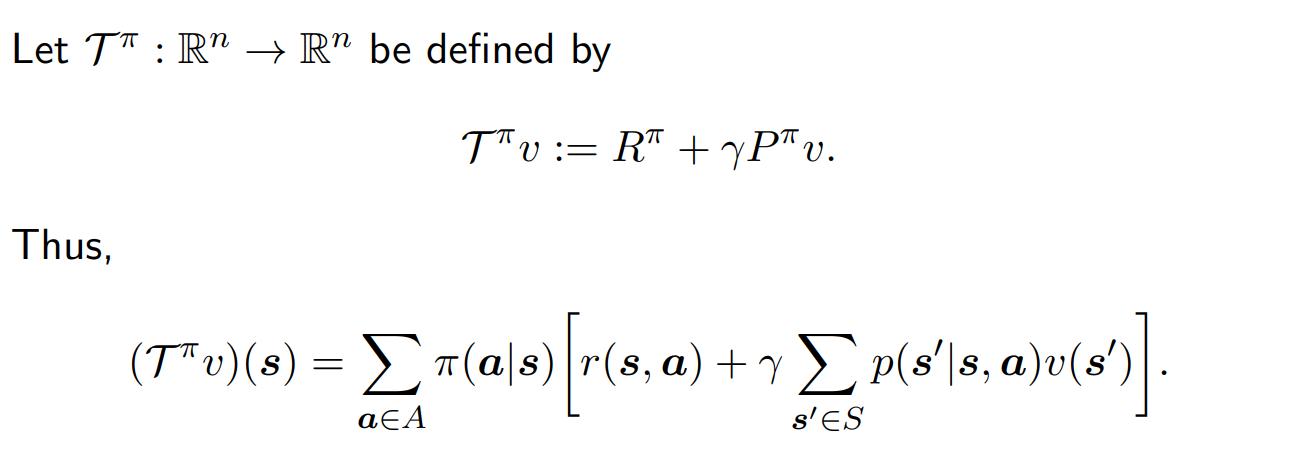
- 이때 아래와 같이 operator를 이용해 나타낼 수 있다.
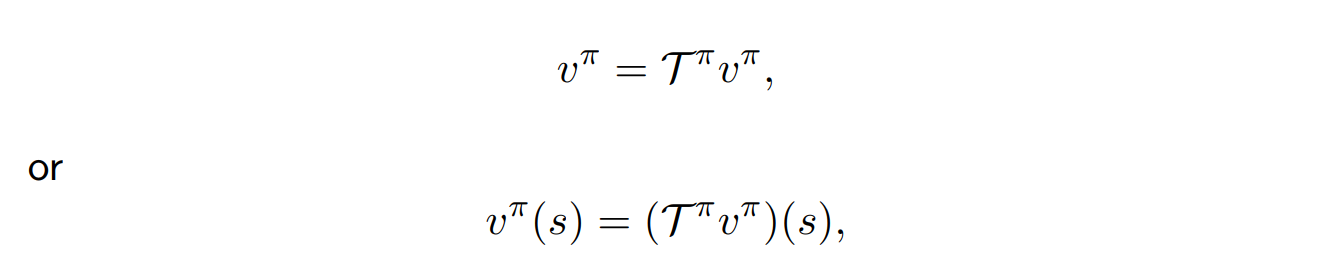
- 를 대입하면 가 나오는 fixed point problem이다.
Bellman Operator
- 앞서 보였던 operator form에 sup을 취해주면, Bellman Operator이다.
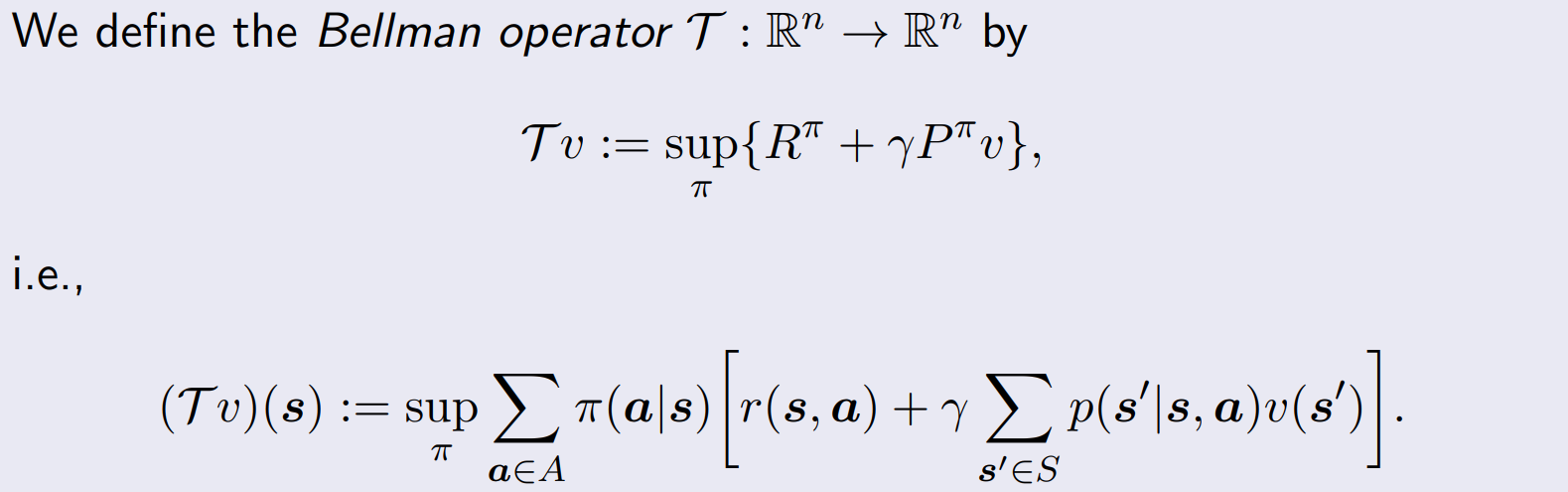
- 아래와 같이 action에 대한 max로 나타낼 수도 있다.
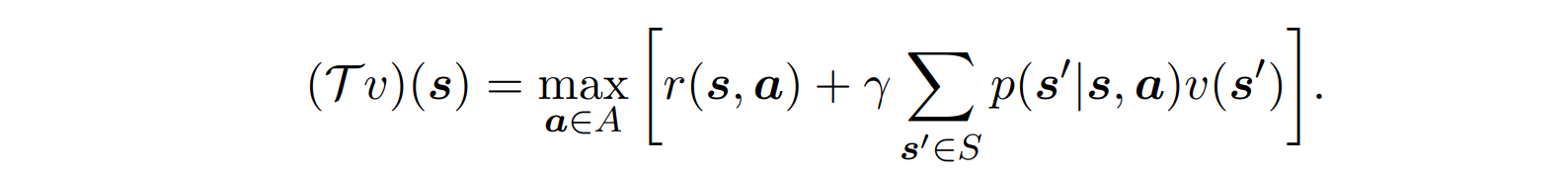
- 증명
- policy의 sup으로 나타낸 식을 (A), action의 max로 나타낸 식을 (B)라고 하자.
- (A)<=(B)

- (A)>=(B)

- 증명
Bellman Equation
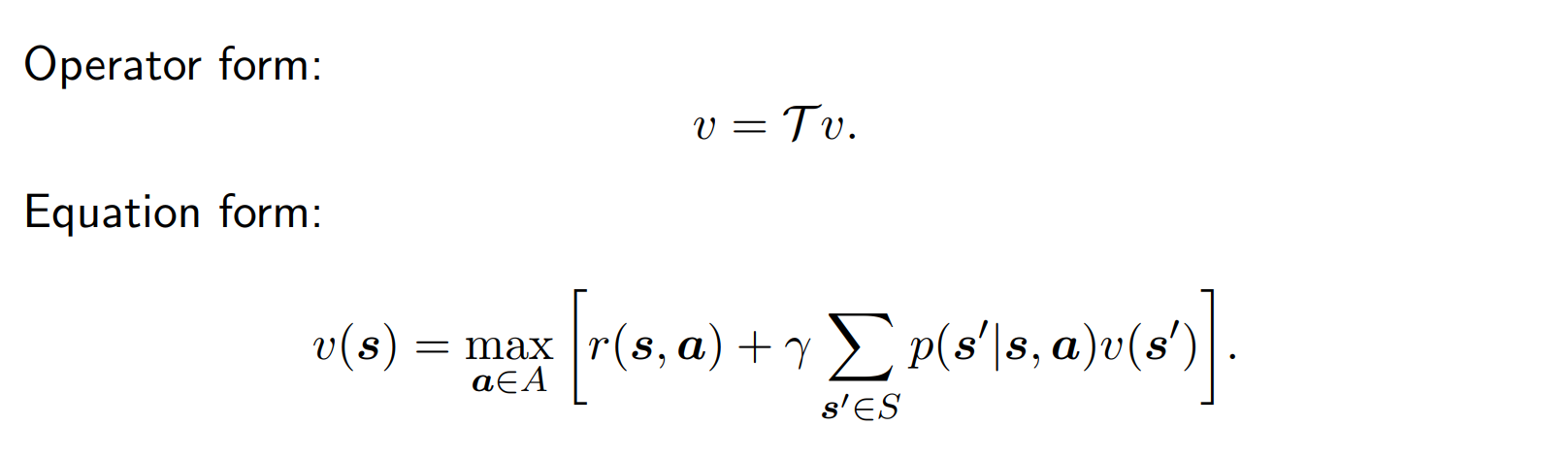
- unique solution이 optimal value function이다.
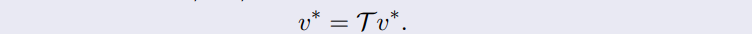
- 증명

- 증명
Value Iteration
contraction property
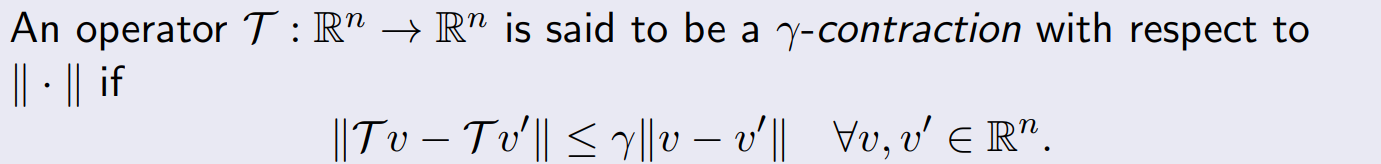
- operator 적용 시, 둘 사이의 간격이 줄어든다.
- 증명
- 아래 식을 이용해서 을 구한다.
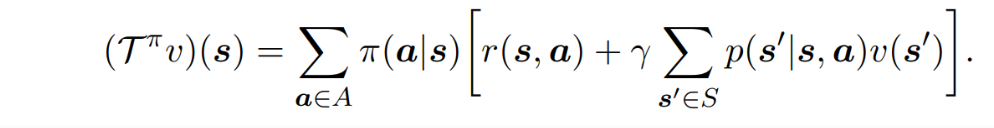
- 이때 양쪽에 sup norm을 취한다.
- 우변에서 을 제외한 부분들은 모두 확률 값으로 0이상 1이하이다. 따라서 만 남기면 크기가 커진다.
- 아래 식을 이용해서 을 구한다.
Monotonicity
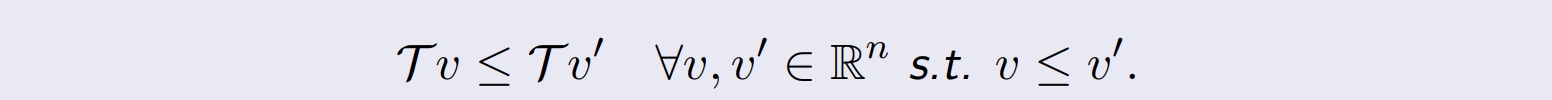
- compinent size( 에 적용됨)
Banach Fixed Point Theorm

-
는 unique fixed point 을 갖는다.
-
에 를 반복 적용하는 value iteration을 수행할 경우, 로 수렴한다.
-
이를 통해 Value Iteration Algorithm for policy evaluation 가능
- 이때까지 하던 policy evaluation 방법과 같음
- 를 임의의 vector 로 초기화 한다.
- 수렴할 때까지 반복 적용한다.
Optimal Policy
- if S, A are finite sets, there exists an optimal policy, which is
- 증명

Policy Iteration
-
value 뿐만 아니라, policy도 같이 돌며 update한다.
-
임의의 로 시작한다.
-
수렴할 때까지 policy evaluation과 policy improvement를 반복한다.
- policy evaluation
- update value by solving this (value iteration이나 matrix inversion 등 활용)
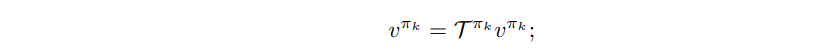
- update value by solving this (value iteration이나 matrix inversion 등 활용)
- policy improvement
- 바로 앞에서 구한 value function을 반영한다.
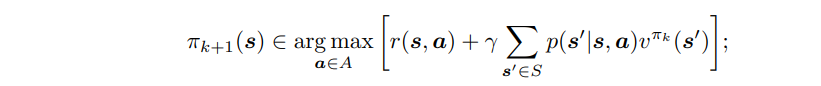
- 바로 앞에서 구한 value function을 반영한다.
- policy evaluation
-
Monotonic Improvement
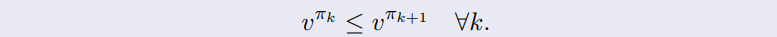
- 다음 차례의 policy가 더 좋은 policy이다.
- 증명
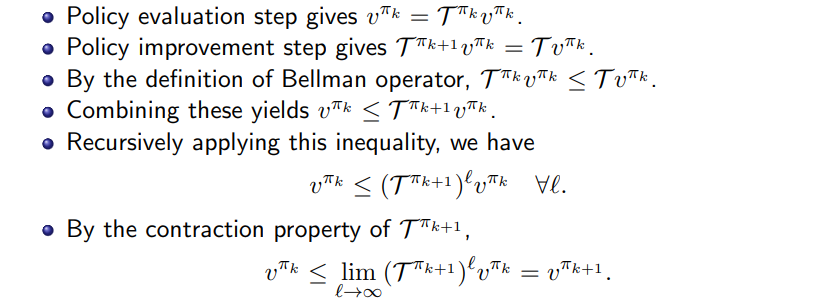
- monotone conergence theorem
으로 monotonically non-decreasing & bouned sequence이면, finite limit를 갖는다.
-
수렴하는 지점이 optimal policy이다.

- 증명

- 증명

정리하신 내용이 많은 도움 되었습니다. 더 자세한 내용을 보고 싶은데, 어떤 강의자료로 공부하셨는지 알 수 있을까요?