[MDP] Finite-Horizon MDPs

구성요소

• finite horizon의 경우 discounting factor $\gamma$를 표시하지 않는다. function 자체가 시간에 따라 변하기 때문이다.
  • 해당 요소를 원할 경우엔 reward function $r_t$ 정의 자체에 포함시킨다.
    e.g. $r_t=r^t*\gamma$

Value Function

• policy $\pi := (\pi_0, ..., \pi_{T-1})$ 이 주어졌다고 가정한다.
• $s_t$로 부터 자체로 reward $r_\tau(s_\tau, a_\tau)$를 더한다.
• 마지막 $s_T$ 이후엔 action 이 없으므로, reward를 $r_\tau(s_\tau)$로 표기한다.
  

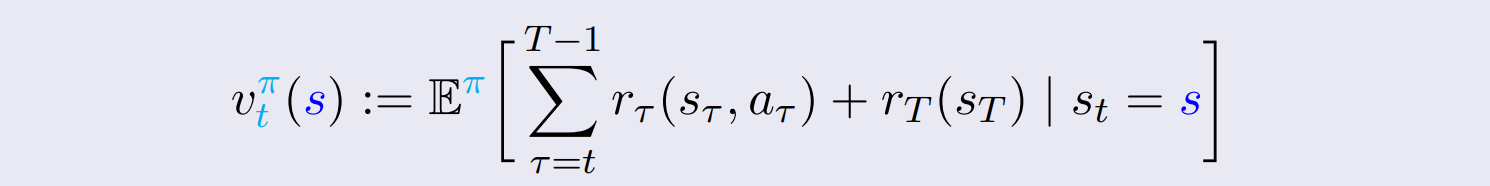
Policy Evaluation

• value function을 immediate reward와 expected value of next state로 나눈다.
  
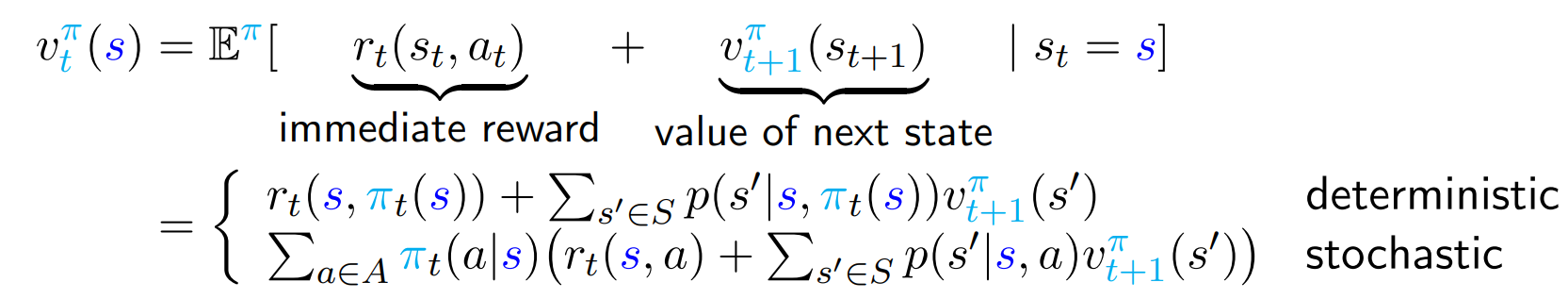
• 마지막 state에서 시작한다.
  마지막엔 다음 action과 stage이 없으므로 value function은 immediate reward이다.
  
• t=T-1 에서부터, t를 하나 씩 빼가며 거꾸로 따라간다.
  계속 반복 시, $v_0$까지 구할 수 있다.

Dynamic Programming Algorithm(optimal policy evauation)

• 마지막 state에서 시작한다.
  마지막엔 다음 action과 stage이 없으므로 value function은 immediate reward이다.
  
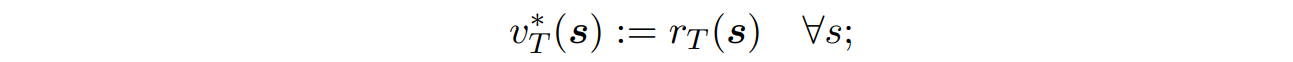
• t=T-1 에서부터, t를 하나 씩 빼가며 거꾸로 따라간다.
  

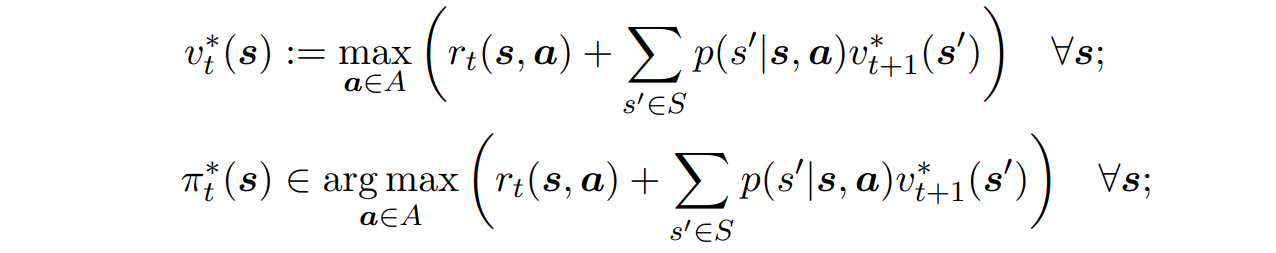
Continuous Control로 확장

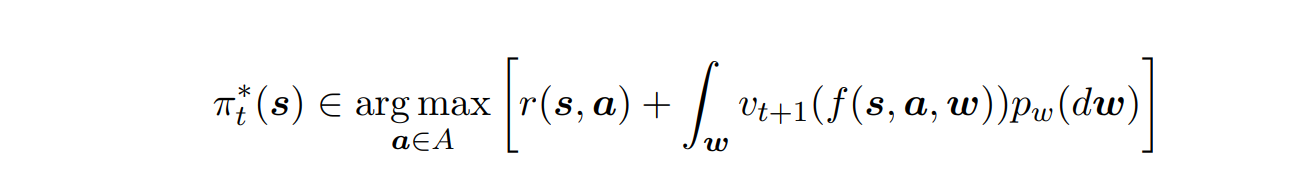
• continuous의 경우, optimal policy의 존재가 보장되지 않는다.
  • 없을 경우, $\epsilon$-optimal policy 사용하기
• 모든 state를 비교할 수 없어서, 일정 간격으로 몇 개 선택해서 비교한다.

+ optimal policy가 stochastic일 수 있을까?

• 가능하다.
• $\argmax_{a \in A}$ 에서 결과로 a가 하나가 아닌 여러 개 나올 때
• 각각에 대해 확률로 표현 e.g. $\pi_t^*(a_2^*|s)=p_2^*$
• 각각의 p는 0보다 크고, 그 합은 1