[선형대수학] 행렬의 개념과 연산

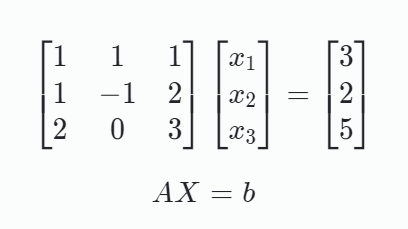
0. Summary

• 행렬(Matrix)은 수나 다항식을 직사각형 모양으로 배열한 것이다.

• 행렬은 선형대수학에서 식을 간략하게 표현하는 역할을 한다.

• 관련 용어

  • identity matrix $I_n$ : $AI_n=A$
  $I_n := \begin{bmatrix} 1&0& \cdots & 0 \\ 0&1& \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots & 1 \end{bmatrix} \in R^{n \times n}$
  • Inverse : $AB=I_n$이면, $B=A^{-1}$
  • Transpose : $A \in R^{m \times n}$와 $B \in R^{n \times m}$에서, $b_{ij}=a_{ji}$이면, $B=A^T$이다.
  • Symmetric matrix : $A=A^T$이면, A는 symmetric하다고 말한다.

• 기본 연산

  • 행렬 간 덧셈 : 차원이 같은 두 행렬에서, 같은 위치의 원소끼리 더한다.
  • 행렬 간 곱셈 : $C_{ij}$ = $A$의 i번째 row와 $B$의 j번째 column의 내적(inner product)
  • 분배법칙과 결합법칙이 성립한다.

• 주요 특징

  $AA^{-1} = I = A^{-1}A \\ (AB)^{-1} = B^{-1}A^{-1} \\ (A+B)^{-1} \ne A^{-1} + B^{-1} \\ (A^T)^T = A \\ (A+B)^T = A^T+B^T \\ (AB)^T = B^TA^T$

• 선형방정식 해 구하기
  • A가 invertible 할 때(n*n 행렬) : $X = A^{-1}b$
  • $A^{-1}A$가 invertible 할 때 : $X = (A^TA)^{-1}A^Tb$
  • 일반적인 경우 : guissian elimination
  • inverse 구하기 : 일반적인 선형방적식 구하는 방법에서, 우측을 identity matrix로 둔다.

---

1. 행렬(Matrix)의 정의

• 행렬이란 수나 다항식을 직사각형 모양으로 배열한 것을 의미한다.
• 사각형의 가로 줄을 row, 세로 줄을 column 이라고 부른다.
• $m$ rows, $n$ columns 로 구성된 행렬 $A \in R^{m \times n}$가 있을 때, 아래와 같이 표현할 수 있다.

• 행렬도 벡터(vector)의 일종으로 볼 수 있다.(행렬 간 덧셈과 스칼라 곱이 가능하다.)

  vector의 정의
  수학적 관점에서, 아래 2가지 성질을 만족하면 모두 벡터로 볼 수 있다.

  • 두 벡터를 서로 더할 수 있다.
  • 벡터들에 scalar를 곱할 수 있다.

2. 행렬의 필요성

• 행렬은 선형대수학(Linear Algebra)에서 핵심적인 역할을 한다.

  • 선형방정식(Linear equation)을 간략히 표현하여 복잡한 연산 및 표현을 돕는다.
    예를 들어, 아래의 (A) 방정식들을 (B)로 표현할 수 있다.
    (A)

    $x_1 + x_2 +x_3 = 3 \\ x_1 - x_2 + 2x_3 = 2 \\ 2x_1 \ \ \ \ \ \ \ + 3x_3 = 5$

    (B)

    $\begin{bmatrix} 1&1&1\\ 1&-1&2\\ 2&0&3 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 3\\2\\5 \end{bmatrix}$
    $AX=b$

  • 행렬은 linear function으로 볼 수도 있다.
    행렬로 나타낸 $AX=b$ 를 A 행렬에 input $X$가 들어가 output $b$가 나온다고 보는 것이다.

  • 데이터 표현/저장 용도로도 사용할 수 있다.

3. 관련 개념 및 용어

• Identity matrix

  • 다른 행렬에 곱하면, 자기 자신이 나오는 행렬을 identity matrix라고 부른다.
    $AI_n=A \\ I_nA=A$
  • 대각선은 모두 1이고, 나머지는 모두 0인 행렬이다.
    $I_n := \begin{bmatrix} 1&0&0& \cdots & 0 \\ 0&1&0& \cdots & 0 \\ 0&0&1& \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \cdots \\ 0&0&0& \cdots & 1 \end{bmatrix} \in R^{n \times n}$

• Inverse

  • $AB=I_n$이면, $B$는 $A$의 역(inverse)이다.
  • $A$의 inverse는 $A^{-1}$로 표기한다.
  • inverse는 $A \in R^{n \times n}$ 일 때만 존재할 수 있다. (column의 수와 row의 수가 같아야 한다.)
    • 모든 n*n matrices가 inverse를 갖는 것은 아니다.

      ✔️ matrix determinant : inverse 존재 여부 판단하기
      $A=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$ 일 때, $A$의 determinant는 $a_{11}a_{22} - a_{12}a_{21}$이다.
      만약 $det(A)=0$ 이면 $A^{-1}$는 존재하고, $det(A) \ne 0$이면 존재하지 않는다.

  • inverse가 존재하면 regular/invertible/nonsingular라고 하고,
    inverse가 존재하지 않으면 singular/noninvertible이라고 한다.

• Transpose

  • $A \in R^{m \times n}$와 $B \in R^{n \times m}$에서, $b_{ij}=a_{ji}$이면, $B=A^T$이다.
  • 예시)
    $A= \begin{bmatrix} 3 & 1\\ 2 & 2 \\ 1 & 3\end{bmatrix}, A^T = \begin{bmatrix} 3 & 2 & 1 \\ 1 & 2 & 3 \end{bmatrix}$

• Symmetric matrix

  • $A=A^T$이면, A는 symmetric하다고 말한다.
  • $A$와 $B$가 모두 symmetric하면
    • $A+B$는 symmetric하다.
    • $AB$는 symmetric하고 말한 수 없다.
      (반례) $\begin{bmatrix} 1&0\\0&0\end{bmatrix}\begin{bmatrix} 1&1\\1&1 \end{bmatrix}=\begin{bmatrix} 1&1\\0&0\end{bmatrix}$

4. 기본 연산

• Addition
  • 같은 위치의 원소끼리 더하기
    $A \in R_{m \times n},\ B \in R_{m \times n}$ 일 때,

• Multiplication (두 행렬 간의 곱)

  • A의 column의 수와 B의 row의 수가 같아야 곱할 수있다.
    • $A \in R^{m \times k}, \ B \in R^{k \times n}$
    • $A \times B = C$라면, $C \in R^{m \times n}$
  • $C_{ij}$ : $A$의 i번째 row와 $B$의 j번째 column의 내적(inner product)이다.
    
  $C_{ij} = a_{i1}b_{i1} + a_{i2}b_{i2} + \cdots + a_{in}b_{in} = \sum_{l=1}^{n}a_{il}b_{li}$
  • $AB \ne BA$

• Associativity

  $(AB)C=A(BC)$

• Distributivity

  $(A+B)C=AC+BC \\ A(C+D)=AC+AD$

5. 주요 특징

6. 선형방정식 해 구하기

• [case 1] A가 invertible (반드시 $A\in R^{n \times n}$)
  $AX=b \\ A^{-1}AX=A^{-1}b \\ I_nX = A^{-1}b \\$
  $\therefore X = A^{-1}b$
• [case 2] $A^{T}A$가 invertible ( $A \notin R^{n \times n}$이어도, $A^TA \in R^{n \times n}$은 늘 성립)
  $A^TAX=A^Tb \\ (A^TA)^{-1}A^TAX=(A^TA)^{-1}A^Tb \\ \therefore X = (A^TA)^{-1}A^Tb$
• [case 3] general case(앞 두가지 모두 해당 안될 때도 포함)

  • Gaussian Elimination 활용

    • 연립 방정식을 특수한 하나의 행렬로 표현한다.
      (예시)

      $-2x_1+4x_2-2x_3-x_4+4x_5 = -3 \\ 4x_1 -8x_2 +3x_3 -3x_4 +x_5 = 2 \\ 1x_1 -2x_2 +x_3 -x_4 +x_5 = 0 \\ 1x_1 -2x_2 -3x_4 +4x_5 = a \\ \downarrow \\ \begin{bmatrix} \begin{array}{rrrrr|r} -2 & 4 & -2 & -1 & 4 & -3\\ 4 & -8 & 3 & -3 & 1 & 2\\ 1 & -2 & 1 & -1 & 1 & 0 \\ 1 & -2 & 0 & -3 & 4 & a \end{array} \end{bmatrix}$

    • 행 간의 곱셈/덧셈을 통해, diagonal(대각선) 부분은 1, diagonal(대각선)의 왼쪽 아래는 0으로 만든다.
      (예시)

      $\begin{bmatrix} 1&a&b \\ 0&1&c \\ 0&0&1 \end{bmatrix}$

    • 다시 다항식으로 바꿔 해를 구한다.
      (예시)

      $\begin{bmatrix} \begin{array}{rrrrr|r} 1 & -2 & 1 & -1 & 1 & 0\\ 0 & 0 & 1 & -1 & 3 & -2\\ 0 & 0 & 0 & 1 & -2 & 1 \\ 0 & 0 & 0 & 0 & 0 & a+1 \end{array} \end{bmatrix} \\ \downarrow \\ x_1-2x_2+x_3-x_4+x_5 = 0 \\ x_3-x_4+3x_5 =-2 \\ x_4-2x_5 = 1 \\ 0=a+1$
• Inverse 구하기
  • 앞의 [case 3]에서와 같이 Gauissian Elimination을 통해 구한다.
  • 행렬의 우측에 identity matrix를 적고, 좌측이 identity matrix가 되게 Gaussian Elimination을 수행하면, 우측이 inverse가 된다.
    (예시)
    $A=\begin{bmatrix} 1&0&2&0 \\ 1&1&0&0 \\ 1&2&0&1 \\ 1&1&1&1 \\ \end{bmatrix}$
    이면
    $\begin{bmatrix} \begin{array}{rrrr|rrrr} 1&0&2&0&1&0&0&0\\ 1&1&0&0&0&1&0&0 \\ 1&2&0&1&0&0&1&0 \\ 1&1&1&1&0&0&0&1 \end{array} \end{bmatrix} \\ \downarrow \\ \begin{bmatrix} \begin{array}{rrrr|rrrr} 1&0&0&0&-1&2&-2&2\\ 0&1&0&0 &1&-1&2&-2\\ 0&0&1&0 &1&-1&1&-1\\ 0&0&0&1 &-1&0&-1&2 \end{array} \end{bmatrix}$
    그 결과
    $A^{-1}= \begin{bmatrix} -1&2&-2&2\\ 1&-1&2&-2\\ 1&-1&1&-1\\ -1&0&-1&2 \end{bmatrix}$