[통계] 확률론 기초

딥러닝은 확률론 기반의 기계학습 이론에 기반을 두고 있다.
기계학습에서 사용되는 손실함수들은 데이터 공간을 통계적으로 해석해서 유도되는 것이다.

따라서 딥러닝을 배우기 전에 알아두어야 할 통계 이론의 기초를 알아보겠다.

1. 기본용어 & 표기법

• 데이터 공간 : X * Y
• 관측 가능한 데이터 : (x, y) ∈ X*Y
• 확률분포(데이터 공간에서 관측가능한 데이터의 분포) : D

2. 확률 변수

• 종류 : 이산확률변수, 연속확률변수

• 분류 방법 : D 기준
  확률변수가 데이터 공간에 의해 결정되는 것으로 오해하는 경우가 있다. 하지만 실제론 확률 분포에 따라 결정된다.
  예를 들어, 데이터 공간이 실수형(연속)이더라도, 실제 분포는 -0.5와 0.5 둘 중 하나를 고르는 것이라면, 이산확률분포이다.

• 모델링
  모델링 방법도 이산형인지 연속형인지에 따라 달라진다.

이산확률변수	연속확률변수

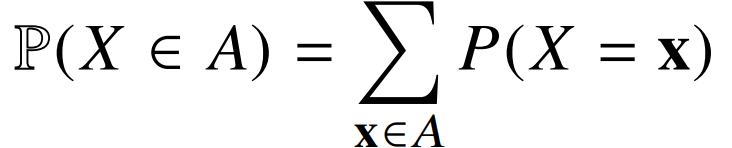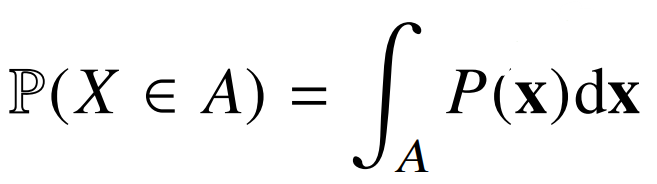3. 결합분포

결합분포란 확률변수가 여러 개인 확률분포를 의미한다.
P(x, y) 표기하곤 한다.

결합분포의 경우 각 확률 변수의 영향을 해석하기 위해
주변확률분포와 조건부확률분포를 이용한다.

A. 주변확률분포

P(x)의 형태로 표기하며, y의 영향을 배제하고 x에 따라 데이터 빈도를 나타낸 것이다.

결합분포 P(x,y)에서 y의 경우의 수를 모두 대입 후 더함으로써, x에 따른 결과를 표현하는 것이다.

이산형	연속형

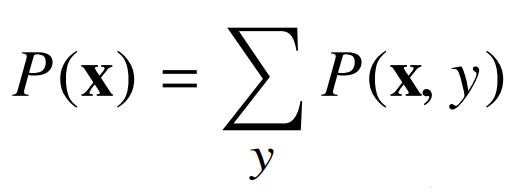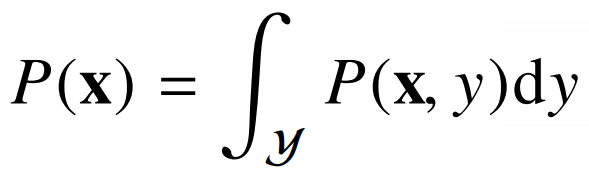반대로 x의 영향을 베제하고 y에 따라서 P(y)를 나타낼 수도 있다.

B. 조건부 확률 분포

P(x|y)의 형태로 표기하며, y 조건에서 x의 분포를 나타낸다.