Counting Inversions

다음 문제를 참고하였습니다.
https://www.acmicpc.net/problem/10090
영어 그대로 순서 대비 크기가 역전되어 있는 것을 세주는 문제입니다. 예를 들어서 1 ~ 7까지의 수에 대해 4 2 7 1 5 6 3 라는 배열이 있다고 할 때,
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
4 2 7 1 5 6 3
총 10개의 케이스가 존재합니다.

접근 방법

Brute Force

그냥 일일이 본인보다 작은 수가 뒤쪽에 몇개가 있는지를 살피면 됩니다. 시간 복잡도는 O(N^2)이고, 따로 설명은 하지 않겠습니다.

Merge Sort

Merge Sort의 진행과정 중간을 살펴보겠습니다.

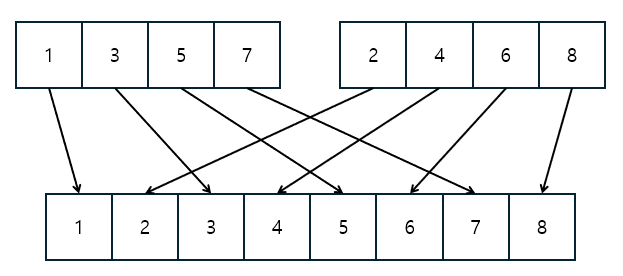
다음과 같이 Merge Sort가 진행되면서 다음과 같은 특징을 볼 수 있습니다.

3과 2 처럼 순서가 맞지 않으면 swap이 일어난다.

즉, 순서가 맞지 않으면 swap이 일어나는데, swap이 된다면 위 그림에서 화살표가 교차합니다.

Merge Sort의 경우 정렬된 배열에서 진행하기에, 실제로 2 화살표와의 교점의 갯수는 3의 오른쪽에 있는 모든 수, 즉 2보다 큰 모든 수 중 2 앞에 있는 수들과 다 만나게 됩니다.

즉 순서가 맞지 않다면, 그 지점의 수만큼 교차점이 발생하게 됩니다.

다시 문제의 예시를 보겠습니다.

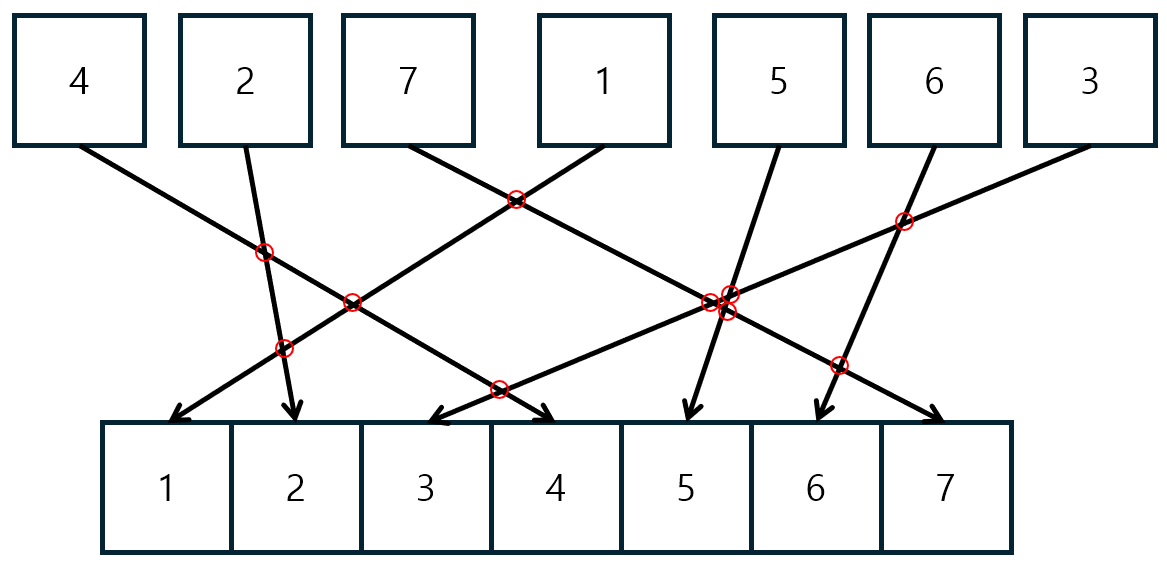
이 문제에서도 역시 교차점의 갯수가 inversion의 갯수 10개임을 알 수 있습니다.

이 방법을 이용해서 위에서 언급한 해당 문제를 풀어보면 다음과 같습니다.

import java.io.*;
import java.util.*;

public class Main {
	static int n;
	static int[] arr, tmpArr;
	static long mergeSort(int start, int end) {
		long result = 0;
		if(start == end) return 0;
		int mid = (start + end) / 2;
		result += mergeSort(start, mid);
		result += mergeSort(mid + 1, end);
		result += merge(start, mid, end);
		return result;
	}
	static long merge(int start, int mid, int end) {
		int i = start, j = mid + 1, k = start;
		long result = 0;
		while(i <= mid && j <= end) {
			if(arr[i] <= arr[j]) {
				tmpArr[k++] = arr[i++];
			} else {
				result += mid - i + 1;
				tmpArr[k++] = arr[j++];
			}
		}
		if(i <= mid) {
			for(int l = i; l <= mid; l++) {
				tmpArr[k++] = arr[l];
			}
		} else {
			for(int l = j; l <= end; l++) {
				tmpArr[k++] = arr[l];
			}
		}
		for(int l = start; l <= end; l++) {
			arr[l] = tmpArr[l];
		}
		return result;
	}
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		n = Integer.parseInt(br.readLine());
		arr = new int[n];
		tmpArr = new int[n];
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		for(int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		System.out.println(mergeSort(0, n - 1));
		br.close();
	}
}

Segment Tree

세그먼트 트리로도 구현이 가능합니다. 구현 전 4 2 7 1 5 6 3에 대해 역전되어 있는 쌍의 수를 다시 한번 살펴보겠습니다.

4 : 0개
4 2 : 1개
4 2 7 : 1개
4 2 7 1 : 4개 (+3)
4 2 7 1 5 : 5개 (+1)
4 2 7 1 5 6 : 6개 (+1)
4 2 7 1 5 6 3 : 10개 (+4)

어떤 새로운 숫자 K가 추가될 때마다 K보다 큰 수의 갯수만큼 추가되는 것을 알 수 있습니다. 이 때 큰 수의 갯수는 반대로 큰 수 기준으로 본인보다 작은 수가 +1 갱신되는 것을 알 수 있습니다. 이는 세그먼트 트리 구간합으로 구할 수 있습니다.

예를 들어 보면 4 2 7 에서 4 2 7 1이 추가되는 상황을 보겠습니다.

K	1	2	3	4	5	6	7
count	0	1	0	1	0	0	1
sum	0	1	1	2	2	2	3

여기서 어떤 수 K가 추가되면 구간합 [K, 7]을 구합니다.
1이 추가된 경우 3이 됩니다.

그리고 이렇게 구간합을 구하고 난 후에는 이제부터 1은 이미 사용되었기 때문에 새로운 수에 대해 무조건 왼쪽에 있습니다. 겹칠 수 있도록 카운트를 증가합니다.

K	1	2	3	4	5	6	7
count	1	1	0	1	0	0	1
sum	1	2	2	3	3	3	4

import java.io.*;
import java.util.*;

public class Main {
	static int n;
	static long[] tree;
	static void update(int node, int s, int e, int idx) {
		if(idx < s || e < idx) return;
		if(s == e) {
			tree[node]++;
			return;
		}
		int mid = (s + e) / 2;
		update(2 * node, s, mid, idx);
		update(2 * node + 1, mid + 1, e, idx);
		tree[node] = tree[2 * node] + tree[2 * node + 1];
	}
	static long get(int node, int s, int e, int ts, int te) {
		if(te < s || e < ts) return 0;
		if(ts <= s && e <= te) return tree[node];
		int mid = (s + e) / 2;
		long left = get(2 * node, s, mid, ts, te);
		long right = get(2 * node + 1, mid + 1, e, ts, te);
		return left + right;
	}
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = null;
		n = Integer.parseInt(br.readLine());
		tree = new long[4 * n];
		long answer = 0;
		st = new StringTokenizer(br.readLine());
		for(int i = 0; i < n; i++) {
			int idx = Integer.parseInt(st.nextToken());
			answer += get(1, 1, n, idx, n);
			update(1, 1, n, idx);
		}
		System.out.println(answer);
		br.close();
	}
}