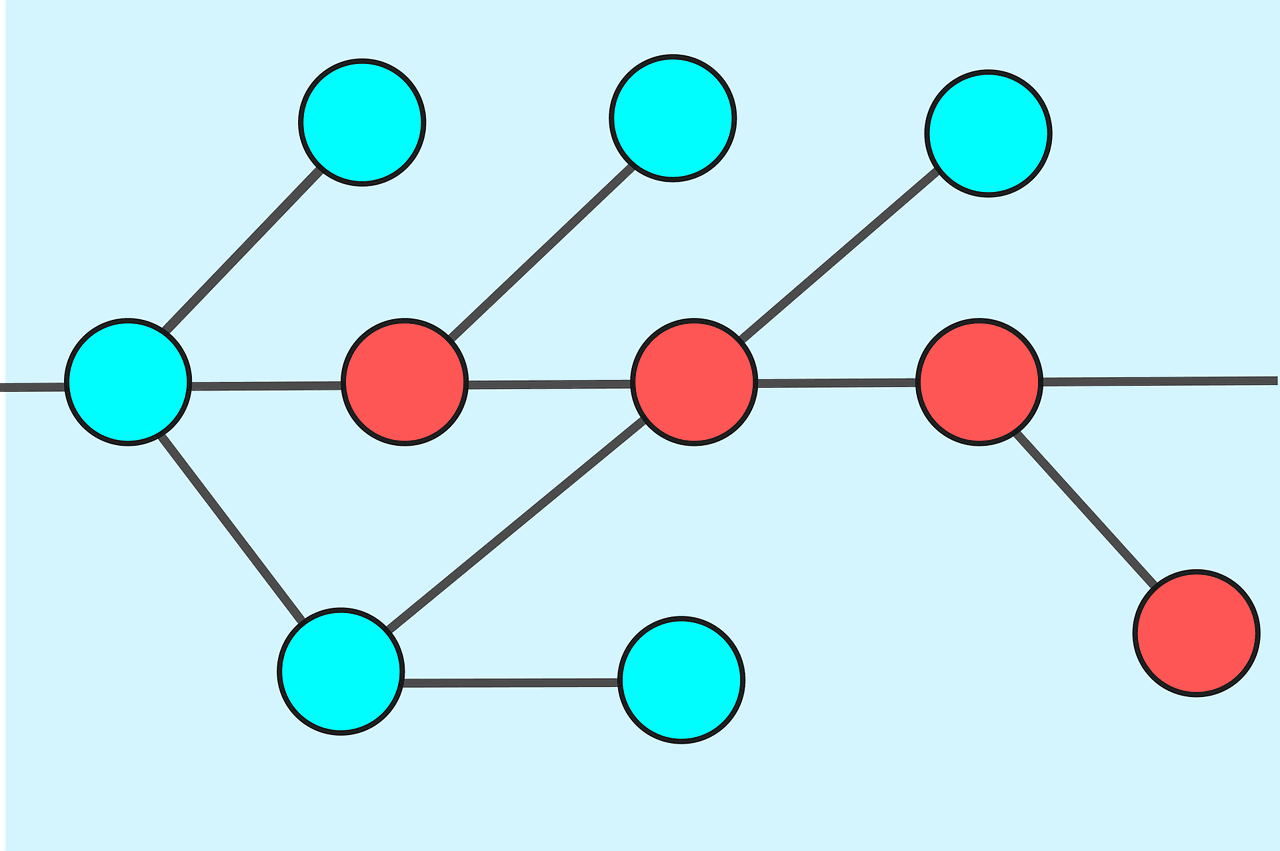
배경

세그먼트 트리가 값이 갱신되는 상황에서 구간합을 구하는 방법임은 익히 알고 있다고 합시다. 그런데 뭔가 더 최적화가 가능할까? 이 상황에서 세그먼트 트리에서 불필요한 연산과 메모리를 더더더 줄일 수 있을까? 에 대한 답이 바로 펜윅 트리(Fenwick Tree) 또는 BIT(Binary Indexed Tree) 입니다.

펜윅 트리

다음과 같은 배열을 하나 생각해봅니다.

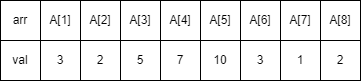
세그먼트 트리를 사용하면 아래 그림과 같이 모든 구간 합을 저장합니다.

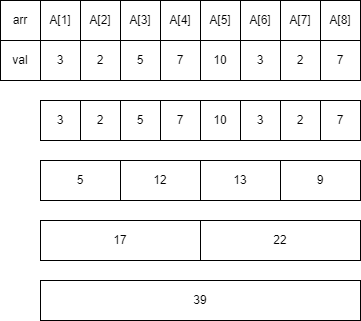
하지만... 잘 생각해보면 큰 것에서 작은 조각(왼쪽) 빼면 오른쪽 조각을 구할 수 있습니다. 예를 들어 [3, 4]의 구간 합은 [1, 4]와 [1, 2]의 차랑 같이에 이 부분 memorization을 할 필요가 없습니다. 따라서 아래와 같이 줄일 수 있습니다.

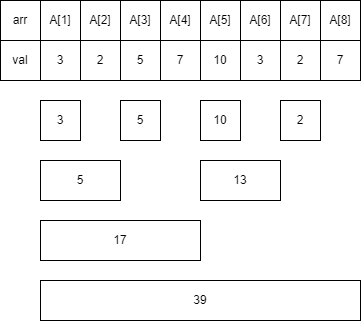
이와 같은 발상에서 출발합니다.

여기서 조금은 어려운 발상을 해보겠습니다. 각 인덱스 i에 대해 마지막 1이 나타내는 값을 L[i]라 두겠습니다.

• 1 = 1(2), L[1] = 1
• 2 = 10(2), L[2] = 2
• 3 = 11(2), L[3] = 1
• 4 = 100(2), L[4] = 4
• 5 = 101(2), L[5] = 1
• 6 = 110(2), L[6] = 2
• 7 = 111(2), L[7] = 1
• 8 = 1000(2), L[8] = 8

그리고 인덱스 i부터 앞으로 L[i] 만큼 범위를 박스로 나타내면 아래와 같습니다.

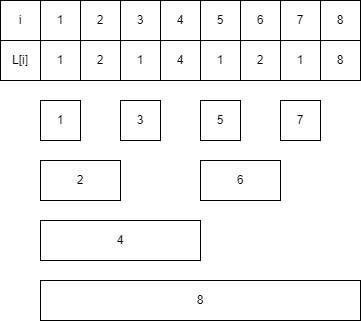
어라? 그림이 익숙합니다. 우리가 딱 원하는 구간이 형성됩니다. 이제 남은 것은 두가지 입니다.

• L[i]를 구하는 방법
• 이 구간들로 실제 구간합을 구하는 방법

마지막 1이 나타내는 값

예를 들어 6 = 110(2)에 대해 생각하면 이 값이 010(2) = 2 가 나와야 합니다.
이를 구하기 위해서는 우선 비트 반전을 생각해볼 수 있습니다.

~(6) = 1111...001(2)가 됩니다.

여기서 우리가 원하는 부분은 뒤쪽이 ...010(2) 로 어떻게 만들어서 & 연산을 취하면 될 것처럼 보입니다. 어떤 방법이 있을까요?

바로 +1을 취하면 됩니다. ~(6) + 1... 이거 익숙합니다. 음수 표현 잘 생각해보면 비트 전체 반전을 시키고 + 1한게 음수 표현인데... 어 그러면 답이 나옵니다.

L[i] = i & -i

왜 이렇게 나오는지 보겠습니다.
우선 원하는 위치보다 왼쪽 부분은 비트 반전이 되기 때문에 어차피 & 연산 취하면 전부 0입니다.
그리고 원하는 위치보다 오른쪽 부분은 원래는 전부 0이고, 이를 반전시키면 전부 1입니다. 그런데 여기에 1을 더해주면 111111...1(2) 형태가 10000...0(2)형태가 됩니다. 딱 맨 앞의 부분, 즉 원하는 위치만 1이 됩니다.

따라서 우리가 원하는 L[i]를 얻을 수 있습니다.

실제 구간합

이제 실제 구간합을 구해보겠습니다.

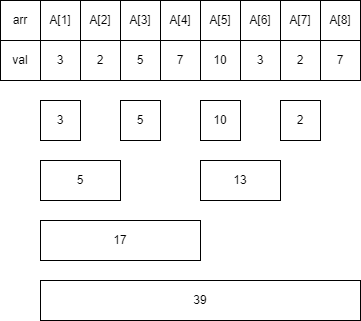
우선 tree 배열을 주어진 N 크기에 맞게 만들 수가 있습니다. tree[i]에 들어가는 값은 다음과 같습니다.

tree[i]는 i부터 L[i]개의 원래 배열 A[i]들의 합입니다.

• tree[1], L[1] = 1, A[1] = 3
• tree[2], L[2] = 2, A[2] + A[1] = A[2] + tree[1] = 5
• tree[3], L[3] = 1, A[3] = 5
• tree[4], L[4] = 4, A[4] + A[3] + A[2] + A[1] = A[4] + tree[3] + tree[2] = 17
• tree[5], L[5] = 1, A[5] = 10
• tree[6], L[6] = 2, A[6] + tree[5] = 13
• tree[7], L[7] = 1, A[7] = 2
• tree[8], L[8] = 8, A[8] + ... + A[1] = A[8] + tree[7] + tree[6] + tree[4] = 39

그리고 A[i] + ... + A[j]를 구하는 방법은 기본적으로 펜윅 트리와 누적합의 기본적인 아이디어인 A[1] + ... + A[j]에서 A[1] + ... + A[i - 1]을 뺀 값으로 구합니다. 즉, sum(j) - sum(i - 1)로 구할 수 있습니다.

sum()

실제 합을 구하는 메소드입니다.

int sum(int i) {
    int ans = 0;
    while (i > 0) {
        ans += tree[i];
        i -= (i & -i);
    }
    return ans;
}

update()

수가 변경이 되면 담당 구간이 모두 업데이트가 됩니다.

void update(int i, int num) {
    while (i <= n) {
        tree[i] += num;
        i += (i & -i);
    }
}

출처

• https://www.acmicpc.net/blog/view/21