문제
다음 문제를 바로 살펴봅시다. 문제 링크
문제에서 처리하는 쿼리들을 정리하면 다음과 같습니다.
1 i x: i번 지역에 x 만큼 추가2 i y: i번 지역에 y 만큼 추가3 L R:[L, R]범위의 지역 수4 T: 내림차순으로 T번째 높이
이거만 보면 일반적인 세그먼트 트리(이하 세그) 문제라 생각할 수 있습니다. k번째 찾는 쿼리라 k번째 찾는 방법을 쓰면 풀릴 것 같습니다.
(단 내림차순이라 N - T + 1 번째를 찾는 것임에 유의)
그런데... 높이 범위가 10의 18승으로... 일반적인 방법으로 저장은 절대 불가능하다는 것을 알 수 있습니다.
방법으로는 오프라인 쿼리를 활용하여 좌표 압축을 진행하는 방법도 있습니다. 쿼리에 나오는 모든 높이를 받아서 이에 해당하는 배열만 만드는 방법입니다.
하지만, 온라인으로 문제를 풀어야 되는 상황이라면...? 트리의 노드를 동적으로 저장해야됩니다. 이를 다이나믹 세그먼트 트리라 합니다.
다이나믹 세그먼트 트리
동작원리는 일반 세그먼트 트리를 잘 안다면 쉽게 이해할 수 있습니다. 딱 두가지만 지키면 됩니다.
- update 시 필요한 곳의 노드만 만들어 주자
- 탐색 했는데 하위 노드 없으면 그냥 return 해주자
일반 세그먼트 트리는 이미 트리를 완전 이진 트리 형태로 다 만들어 놓고 거기에서 값만 변경하는 방식입니다.
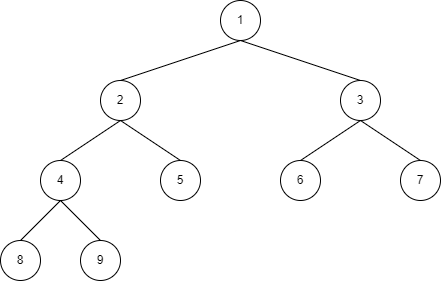
하지만 다이나믹 세그먼트 트리는 update 쿼리 수행시 필요한 곳에서만 노드를 만들어 주고 있기에 이진 트리는 이진 트리인데 완전 이진 트리는 아니고 많이 비어 있는 모습을 띄게 됩니다.
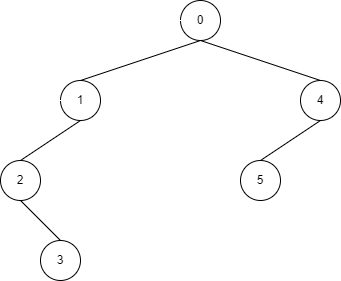
이렇게 필요한 부분만 만들기에 메모리를 많이 절약할 수 있게 됩니다.
그리고 눈치가 빠른 분들은 기본 세그의 노드 번호는 고정이 되어있지만, 다이나믹 세그 노드 번호는 이와 다르다는게 보일겁니다(사진상의 노드 번호가 보면 서로 다릅니다.)
이는 노드가 새롭게 부여될 때마다 노드 번호가 증가하는 방식입니다. 그래서 노드 번호는 할당된 순으로 부여됩니다.
따라서 노드 선언할 때 값 뿐만 아니라 왼쪽과 오른쪽 노드 정보도 같이 들고 있어야 한다는 것이 핵심입니다.
구현
이 구현은 JusticeHui님의 구현 방식을 많이 참고하였습니다. 자바로 구현한 포스팅은 못보았기에 구현해보게 되었습니다.
Node
우선 Node를 정의합니다.
class Node {
long val = 0;
int l = -1, r = -1;
}그리고 Node를 관리할 리스트를 만들어 둡니다.
int size = 1; // 초기 트리는 루트 노트 딱 하나만 존재
List<Node> tree;// 초기화 시
tree = new ArrayList<>();
tree.add(new Node()); // 루트 노드 저장즉 필요한 노드만 관리하고, 노드 내에서 저장을 해당하는 노드의 인덱스를 저장하는 방식을 택합니다. 여기서는 root는 0번 노드로 설정했으며, -1은 노드가 할당되지 않음을 의미합니다.
update
우선 기존 세그입니다.
void update(int node, int s, int e, int idx, long val) {
if(e < idx || idx < s) return;
if(s == e) {
tree[node] += val;
return;
}
int mid = (s + e) / 2;
update(2 * node, s, mid, idx, val);
update(2 * node + 1, mid + 1, e, idx, val);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}위 코드는 update 하기 위해서 양쪽 모두를 탐색하고 있습니다. 하지만 다이나믹 세그의 경우는 필요한 곳만 할당하기에 탐색 과정에서 조건문을 하나 추가로 적어줍니다.
void update(int node, long s, long e, long idx, long val) {
if(s == e) {
tree.get(node).val += val;
return;
}
long mid = (s + e) / 2;
if(idx <= mid) {
if(tree.get(node).l < 0) {
tree.add(new Node());
tree.get(node).l = size++;
}
update(tree.get(node).l, s, mid, idx, val);
} else {
if(tree.get(node).r < 0) {
tree.add(new Node());
tree.get(node).r = size++;
}
update(tree.get(node).r, mid + 1, e, idx, val);
}
int left = tree.get(node).l;
int right = tree.get(node).r;
long lval = left < 0 ? 0 : tree.get(left).val;
long rval = right < 0 ? 0 : tree.get(right).val;
tree.get(node).val = lval + rval;
}get
get은 비슷하지만 없는 노드가 나오면 탐색을 중단한다는 점만 조심하면 됩니다.
long getTotal(int node, long s, long e, long ts, long te) {
if(node < 0) return 0;
if(e < ts || te < s) return 0;
if(ts <= s && e <= te) return tree.get(node).val;
long mid = (s + e) / 2;
long left = getTotal(tree.get(node).l, s, mid, ts, te);
long right = getTotal(tree.get(node).r, mid + 1, e, ts, te);
return left + right;
}T번째 항목 얻기
이게 처음 생각하면 잘 생각이 안날껀데 의외로 기존 세그와 비슷합니다. 다만, 없는 노드는 탐색하지 않는다는 점만 주의하면 됩니다.
long getTth(int node, long s, long e, long t) {
if (s == e) return s;
long mid = (s + e) / 2;
long lval = (tree.get(node).l < 0) ? 0 : tree.get(tree.get(node).l).val;
if (lval >= t) return getTth(tree.get(node).l, s, mid, t);
return getTth(tree.get(node).r, mid + 1, e, t - lval);
}문제 풀이
14577 일기 예보 - P3
import java.io.*;
import java.util.*;
public class Main {
static class Node {
long val = 0;
int l = -1, r = -1;
}
static int N, M, size;
static final long MAX_VALUE = (long) 1e18;
static long[] arr;
static List<Node> tree;
static void update(long idx, long val) {
update(0, 0, MAX_VALUE, idx, val);
}
static long getTotal(long l, long r) {
return getTotal(0, 0, MAX_VALUE, l, r);
}
static long getTth(long t) {
return getTth(0, 0, MAX_VALUE, t);
}
static void update(int node, long s, long e, long idx, long val) {
if(s == e) {
tree.get(node).val += val;
return;
}
long mid = (s + e) / 2;
if(idx <= mid) {
if(tree.get(node).l < 0) {
tree.add(new Node());
tree.get(node).l = size++;
}
update(tree.get(node).l, s, mid, idx, val);
} else {
if(tree.get(node).r < 0) {
tree.add(new Node());
tree.get(node).r = size++;
}
update(tree.get(node).r, mid + 1, e, idx, val);
}
int left = tree.get(node).l;
int right = tree.get(node).r;
long lval = left < 0 ? 0 : tree.get(left).val;
long rval = right < 0 ? 0 : tree.get(right).val;
tree.get(node).val = lval + rval;
}
static long getTotal(int node, long s, long e, long ts, long te) {
if(node < 0) return 0;
if(e < ts || te < s) return 0;
if(ts <= s && e <= te) return tree.get(node).val;
long mid = (s + e) / 2;
long left = getTotal(tree.get(node).l, s, mid, ts, te);
long right = getTotal(tree.get(node).r, mid + 1, e, ts, te);
return left + right;
}
static long getTth(int node, long s, long e, long t) {
if (s == e) return s;
long mid = (s + e) / 2;
long lval = (tree.get(node).l < 0) ? 0 : tree.get(tree.get(node).l).val;
if (lval >= t) return getTth(tree.get(node).l, s, mid, t);
return getTth(tree.get(node).r, mid + 1, e, t - lval);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = null;
st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
size = 1;
arr = new long[N + 1];
tree = new ArrayList<>();
tree.add(new Node());
st = new StringTokenizer(br.readLine(), " ");
for(int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
update(arr[i], 1);
}
int q, idx;
long val, l, r, t;
while(M-- > 0) {
st = new StringTokenizer(br.readLine(), " ");
q = Integer.parseInt(st.nextToken());
switch(q) {
case 1:
idx = Integer.parseInt(st.nextToken());
val = Long.parseLong(st.nextToken());
update(arr[idx], -1);
arr[idx] += val;
update(arr[idx], 1);
break;
case 2:
idx = Integer.parseInt(st.nextToken());
val = Long.parseLong(st.nextToken());
update(arr[idx], -1);
arr[idx] -= val;
update(arr[idx], 1);
break;
case 3:
l = Long.parseLong(st.nextToken());
r = Long.parseLong(st.nextToken());
sb.append(getTotal(l, r)).append('\n');
break;
case 4:
t = Long.parseLong(st.nextToken());
sb.append(getTth(N - t + 1)).append('\n');
break;
}
}
System.out.print(sb);
br.close();
}
}