개요

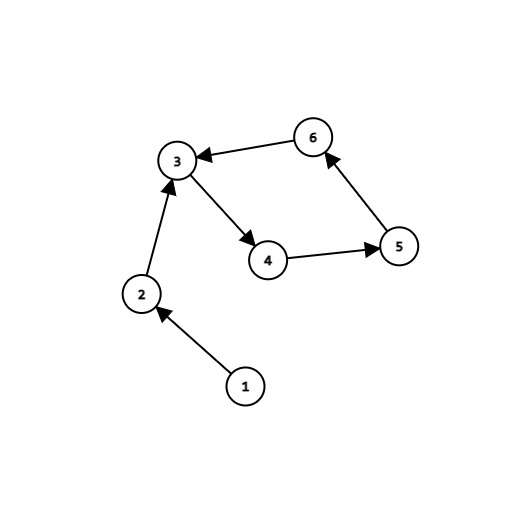
위와 같은 그래프에서 특정 정점 v에서 시작해서 n 번 이동 했을 때 도착하는 정점을 구하는 문제를 생각해보겠습니다.

일반적인 생각은 한 칸 단위로 이동하는 방법입니다. 이 방법은 쿼리당 시간 복잡도가 O(n) 입니다.

하지만, 쿼리가 많아지고, n 이 커진다면 최적화가 필요합니다. 이를 최적화 하는 방법이 있는데, 바로 희소 배열(Sparse Table)을 사용하는 방법입니다.

희소 배열

접근 방법

해당 문제 최적화 방법으로 제일 먼저 떠올릴 수 있는 것은 바로 DP의 memorization 입니다. 초기에 이동에 따른 결과를 다 저장 해놓고 쿼리 나올 때마다 꺼내서 쓰는 겁니다.

우선 아래와 같이 정의합니다.

table[i][j] : j 정점에서 i 만큼 이동했을 때의 결과(정점)

그리고 i 번 이동은 i - 1 에서 한 번 이동한 것과 같으므로 다음과 같은 점화식이 성립합니다.

table[i][j] := table[i - 1][table[i - 1][j]]

이를 이용해서 테이블을 채우면 다음과 같습니다.

	v = 1	v = 2	v = 3	v = 4	v = 5	v = 6
n = 1	2	3	4	5	6	3
n = 2	3	4	5	6	3	4
n = 3	4	5	6	3	4	5
n = 4	5	6	3	4	5	6

하지만 우리는 n 이 클 때가 문제가 됩니다. 정점의 수도 많아지고 n 도 커지면, 이를 저장하는 것이 문제가 됩니다. 가장 큰 문제는 무엇일까요?

n 이동할 때 바로 한 칸만 이동하는 것이 문제입니다. 한 칸 대신 두 칸, 세 칸, … 조금 더 큰 단위로 이동하면 좋을 것 같습니다. 하지만 상수 단위는 또 n 이 커지면 의미가 없습니다. 확실하게 줄이려면 배수 단위가 필요합니다. 가장 대표적으로 떠올릴 수 있는 방법은 이진수를 활용하는 겁니다.

예를 들어 7 = 111(2) = 4 + 2 + 1 , 12 = 1100(2) = 8 + 4 와 같이 모든 수는 2의 거듭 제곱 꼴로 나타내는 것입니다.

그렇다면 테이블은 아래와 같이 바뀝니다.

	v = 1	v = 2	v = 3	v = 4	v = 5	v = 6
n = 1	2	3	4	5	6	3
n = 2	3	4	5	6	3	4
-	-	-	-	-	-	-
n = 4	5	6	3	4	5	6

하지만 1, 2, 4, 8, … 띄엄띄엄 있는 것이 불편합니다. 이를 해결하기 위해 로그를 씌워보겠습니다.

	v = 1	v = 2	v = 3	v = 4	v = 5	v = 6
log1 = 0	2	3	4	5	6	3
log2 = 1	3	4	5	6	3	4
log4 = 2	5	6	3	4	5	6

우리가 아는 배열 인덱스 형태로 0, 1, 2 단위로 되는 것을 알 수 있습니다. 이렇게 만들어진 배열을 우리가 희소 배열(Sparse Table) 이라 합니다.

이 때, 이진수의 덧셈으로 이루어지므로 조회하는데 시간 복잡도는 n 을 이진수로 표현했을 때의 자릿수, 즉 O(log(n)) 이 됩니다.

구현

크기

n 을 이진수로 나타내면 log(n) + 1 자리가 됩니다. (8 = 1000(2) → 4자리)

size = log(n) 으로 두고, 다음과 같이 표현합니다.

int[][] table = new int[size + 1][n + 1];

테이블 초기화

0 행을 우선 초기화합니다. 이는 한 칸 이동이기 때문에 기존에 하던 완전 탐색을 돌리면 됩니다.

그리고 아래 점화식은 여전히 성립합니다.

table[i][j] := table[i - 1][table[i - 1][j]]

이를 활용해서 초기화를 진행하면 다음과 같습니다.

void init() {
	// 1번 이동
	for(int i = 1; i <= n; i++) {
		table[0][i] = arr[i]; // 완전 탐색을 통해 얻은 결과 arr
	}
	
	// 2번 이상 이동
	for(int i = 1; i <= size; i++) {
		for(int j = 1; j <= n; j++) {
			table[i][j] = table[i - 1][table[i - 1][j]];
		}
	}
}

쿼리

이를 사용하는 대표적인 문제로는 최소 공통 조상(Least Common Ancestor, LCA)이 있습니다.

LCA에서는 역순으로 진행할 필요가 있어서, 예시 코드 역시 역순으로 작성하였습니다.

// v 정점에서 n번 이동 결과
int query(int n, int v) {
	// 이동 단위 역순으로 진행
	for(int i = size; i >= 0; i--) {
		if((n & (1 << i)) != 0) {
			v = table[i][v];
		}
	}
	return v;
}

최소 공통 조상(Lowest Common Ancestor, LCA)

이를 사용하는 가장 대표적인 문제가 바로 LCA 입니다.

LCA란 트리에서 두 정점의 공통 부모 노드 중 가장 낮은 계층에 있는 노드를 찾는 문제입니다.

특히, 트리에서 두 정점을 잇는 경로는 유일한데, 이 경로는 무조건 LCA를 지납니다. 다른 말로, 희소 배열을 사용해서 정점 정보 뿐만 아니라 간선 비용 정보 등을 저장하는 것도 따로 만드는 등의 응용을 통해 트리에서의 쿼리 문제를 해결이 가능합니다.

[BOJ] 11438 / LCA 2

• Java 해설 코드

  import java.io.*;
  import java.util.*;
  
  public class Main {
  	static int N, M, size;
  	static int[] depth;
  	static int[][] dp;
  	static List<Integer>[] tree;
  	static void dfs(int node, int d) {
  		depth[node] = d;
  		for(int next : tree[node]) {
  			if(depth[next] == 0) {
  				dfs(next, d + 1);
  				dp[0][next] = node;
  			}
  		}
  	}
  	
  	static int lca(int a, int b) {
  		int d, node1, node2;
  		if(depth[a] > depth[b]) {
  			d = depth[a] - depth[b];
  			node1 = a;
  			node2 = b;
  		} else {
  			d = depth[b] - depth[a];
  			node1 = b;
  			node2 = a;
  		}
  		
  		for(int i = size; i >= 0; i--) {
  			if((d & (1 << i)) != 0) {
  				node1 = dp[i][node1];
  			}
  		}
  		
  		if(node1 == node2) return node1;
  		for(int i = size; i >= 0; i--) {
  			if(dp[i][node1] != dp[i][node2]) {
  				node1 = dp[i][node1];
  				node2 = dp[i][node2];
  			}
  		}
  		
  		return dp[0][node1];
  	}
  	
  	public static void main(String[] args) throws Exception {
  		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
  		StringTokenizer st = null;
          
  		N = Integer.parseInt(br.readLine());
  		depth = new int[N + 1];
  		size = (int)Math.ceil(Math.log(N) / Math.log(2));
  		dp = new int[size + 1][N + 1];
  		tree = new List[N + 1];
  		for(int i = 1; i <= N; i++) {
  			tree[i] = new ArrayList<>();
  		}
          
  		for(int i = 0; i < N - 1; i++) {
  			st = new StringTokenizer(br.readLine(), " ");
  			int a = Integer.parseInt(st.nextToken());
  			int b = Integer.parseInt(st.nextToken());
  			tree[a].add(b);
  			tree[b].add(a);
  		}
          
  		dfs(1, 1);
  		for(int i = 1; i <= size; i++) {
  			for(int j = 1; j <= N; j++) {
  				dp[i][j] = dp[i - 1][dp[i - 1][j]];
  			}
  		}
          
  		M = Integer.parseInt(br.readLine());
  		StringBuilder sb = new StringBuilder();
  		for(int i = 0; i < M; i++) {
  			st = new StringTokenizer(br.readLine());
  			int a = Integer.parseInt(st.nextToken());
  			int b = Integer.parseInt(st.nextToken());
  			sb.append(lca(a, b)).append('\n');
  		}
          
  		System.out.print(sb);
  		br.close();
  	}
  }