배경
구간합을 빠르게 구하는 방법은 무엇일까?
에 대한 답으로는 가장 쉽게 생각할 수 있는 것은 누적합이 있습니다. 누적합을 처음에 초기화 할 때 시간복잡도 O(N)이 걸리지만, 구간합을 구하려면 두 누적합의 차만 구하면 되므로 O(1)으로 구간합을 빠르게 구할 수 있습니다.
하지만 계속 값이 수정된다면 어떨까?
라면 누적합의 경우 계속 초기화해줘야되므로 시간복잡도 O(N)이 걸리게 됩니다. 이걸 줄일 수 있는 방법이 바로 세그먼트 트리입니다. 결론부터 이야기하면 세그먼트 트리는 수정, 조회 모두 O(logN)으로 가능합니다.
세그먼트 트리
초기 배열을 arr = {1, 2, 3, 4, 5}로 놓고 하겠습니다.
세그먼트 트리의 경우에는 다음 arr를 이등분해서 leaf node에는 단 하나의 원소만 남도록 합니다. 세그먼트 트리에 들어가는 구간은 다음과 같습니다.
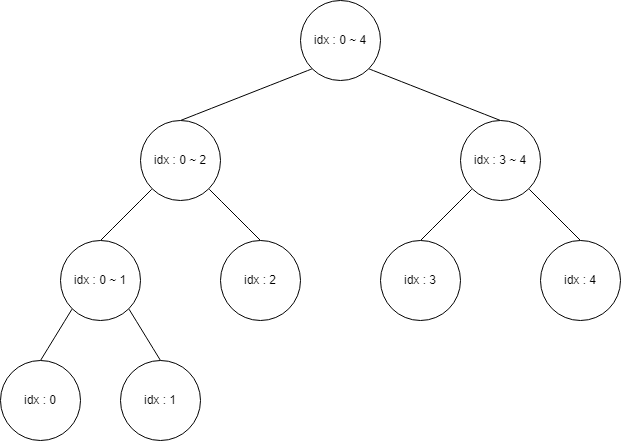
보면 아시겠지만, heap 구현할 때도 사용했던 완전 이진 트리의 형태를 띄고 있습니다.
완전 이진 트리는 배열로 구현이 가능하므로, 트리의 인덱스, 즉 각 노드 번호를 다음과 같이 설정 가능합니다.
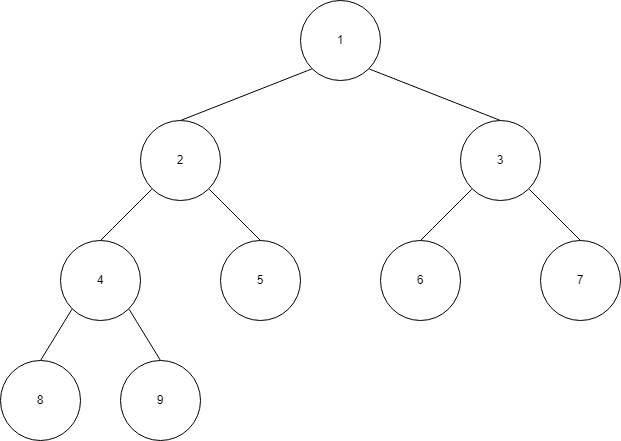
트리의 구현
완전 이진 트리의 경우 배열로 구현이 가능합니다. 포화 이진 트리 상태를 가정했을 때 높이 H에 대해서 마지막 노드의 번호는 (1 << (H + 1)) - 1을 만족합니다. 즉 배열은 다음과 같이 만들어 줄 수 있습니다.
long[] tree = new long[1 << (H + 1)];위의 사례의 경우 트리의 높이 H = 3을 만족하고 이는 리프 노드 갯수 N에 대해서 H = ⌈logN⌉을 만족합니다. 정리하면 다음과 같이 작성 가능합니다.
int H = (int) Math.ceil(Math.log(N) / Math.log(2));
long[] tree = new long[1 << (H + 1)];init()
다양한 구현 방법이 있는데, 어떤 자료는 init(), query(), update()로 구분을 하는 경우도 있습니다. 저의 경우에는 직관성을 위해 init(), get(), update() 로 진행하겠습니다.
init()은 처음에 세그먼트 트리를 만드는 과정입니다. 다음과 같은 논리로 구현이 가능합니다.
부모 노드에 들어갈 구간합은 두 자식 노드의 구간합의 합이다
tree[node] = tree[2 * node] + tree[2 * node + 1]
그리고 자식 노드의 경우도 그 자식의 노드에 대해서 동일한 로직으로 구현 가능합니다. 이는 분할 정복으로 구현이 가능합니다.
필요한 파라미터로는 기본적인 배열과 트리 배열 뿐만 아니라 현재의 노드, 우리가 구하고자 하는 구간 [start, end]가 필요합니다.
void init(long[] arr, long[] tree, int node, int start, int end) {
if(start == end) { // 리프 노드
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
init(arr, tree, 2 * node, start, mid); // 왼쪽 탐색
init(arr, tree, 2 * node + 1, mid + 1, end); // 오른쪽 탐색
tree[node] = tree[2 * node] + tree[2 * node + 1];
}get()
query()라는 것으로도 많이 표현하는데, 구간합 값을 구한다는 의미에서 get()이 직관적이라 저는 get()으로 많이 쓰고 있습니다.
구간 [left, right]에서 구간합을 구한다면 다음과 같이 접근이 가능합니다.
- 루트 노드부터 탐색을 시작합니다. 해당 노드가 가지는 구간 범위는
[start, end]입니다. - 총 4가지 상황이 나오게 됩니다.
- 구할 구간
[left, right]가 노드 구간[start, end]이 겹치지 않음left > end || right < start- 탐색 종료, 애초에 보면 안되는 구간이므로
0반환
- 구할 구간
[left, right]가 노드 구간[start, end]을 포함left <= start && end <= right- 탐색 종료, 더 이상 탐색은 비효율적,
tree[node]반환
- 구할 구간
[left, right]이 노드 구간[start, end]에 포함start <= left && right <= end- 탐색 계속 하기, 헷갈리면 루트 노트에서 처음 시작하는 상황 생각해보자
- 구할 구간
[left, right]가 노드 구간[start, end]이 겹치지 않음나머지 경우- 탐색 계속 하기
- 구할 구간
역시 분할 정복으로 구현 가능합니다.
long get(long[] tree, int node, int start, int end, int left, int right) {
if(left > end || right < start) return 0;
if(left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
long lsum = get(tree, 2 * node, start, mid, left, right);
long rsum = get(tree, 2 * node + 1, mid + 1, end, left, right);
return lsum + rsum;
}update()
update()에서는 값을 변경해줍니다. 바로 arr[index]를 val로 변경합니다.
index 위치의 배열에 있는 수를 변경하려면 다음과 같은 과정을 거칩니다.
- 차이
diff = val - arr[index]를 구합니다. - 루트 노드부터 탐색을 시작합니다. 해당 노드가 가지는 구간 범위는
[start, end]입니다. - 총 2가지 상황이 나오게 됩니다.
index < start || end < index(범위 미포함) : 탐색 중단start <= index && index <= end(범위 포함) : 탐색 진행
void updateTree(long[] tree, int node, int start, int end, int index, int diff) {
if(index < start || end < index) return;
if(start == end) { // start == index == end
tree[node] += diff;
return;
}
int mid = (start + end) / 2;
updateTree(tree, 2 * node, start, mid, index, diff);
updateTree(tree, 2 * node + 1, mid + 1, end, index, diff);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}
void update(long[] tree, int node, int start, int end, int index, long val) {
long diff = val - arr[index];
arr[index] = val;
updateTree(node, start, end, index, diff);
}백준 2042 구간 합 구하기
https://www.acmicpc.net/problem/2042
세그먼트 트리를 적용하여 다음 문제를 아래와 같이 해결 가능합니다.
import java.io.*;
import java.util.*;
public class Main {
static long[] arr, tree;
static void init(int node, int start, int end) {
if(start == end) {
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
init(2 * node, start, mid);
init(2 * node + 1, mid + 1, end);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}
static long get(int node, int start, int end, int left, int right) {
if(right < start || left > end) return 0;
if(left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
long lsum = get(2 * node, start, mid, left, right);
long rsum = get(2 * node + 1, mid + 1, end, left, right);
return lsum + rsum;
}
static void updateTree(int node, int start, int end, int index, long diff) {
if(index < start || end < index) return;
if(start == end) {
tree[node] += diff;
return;
}
int mid = (start + end) / 2;
updateTree(tree, 2 * node, start, mid, index, diff);
updateTree(tree, 2 * node + 1, mid + 1, end, index, diff);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}
static void update(int node, int start, int end, int index, long val) {
long diff = val - arr[index];
arr[index] = val;
updateTree(node, start, end, index, diff);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = null;
st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int H = (int) (Math.ceil(Math.log(N) / Math.log(2)));
arr = new long[N + 1];
tree = new long[1 << (H + 1)];
for(int i = 1; i <= N; i++) {
arr[i] = Long.parseLong(br.readLine());
}
init(1, 1, N);
for(int i = 0; i < M + K; i++) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
switch(a) {
case 1:
long val = Long.parseLong(st.nextToken());
update(1, 1, N, b, val);
break;
case 2:
int c = Integer.parseInt(st.nextToken());
sb.append(get(1, 1, N, b, c)).append('\n');
break;
}
}
System.out.println(sb.toString());
br.close();
}
}