세그먼트 트리의 활용

Segment Tree의 경우 다양한 곳에 활용될 수 있습니다. 다만, 이를 활용하는 것은 숙련도를 요하는데, 이 중 가장 대표적인 것이 세그먼트 트리에서의 K번째 수 찾기가 있습니다.

문제 상황

문제 (BOJ 1572)

https://www.acmicpc.net/problem/1572
좋은 예시가 되는 문제입니다. 이 문제의 경우 뭔가 가운데를 말해요 같이 중간값을 계속 출력하는 구조를 띄는데 차이점이 있습니다.

지금부터 최근 K초 까지 온도의 중앙값을 표시

즉 중간중간에 삭제를 진행하면서 계속 값이 들어오는 상황입니다. 가운데를 말해요의 경우 힙을 사용하는데, 힙의 최대 단점은 힙 중간 값을 삭제하는 것이 (lazy하게 처리하면 가능하긴 하지만) 빡셉니다. 물론 TreeSet과 같은 BBST를 지원하는 자료구조를 활용할 수도 있지만, 기존의 세그먼트 트리에서 약간 변경하면 쉽게 접근 가능합니다.

아이디어

기존 세그먼트 트리는 배열 하나의 크기 N에 대해서 트리의 크기를 1 << h만큼 만들어서 진행을 했습니다. 그리고 [0, N - 1]부터 시작해서 구간합을 쪼개서 트리 노드에 저장하는 방식을 취했습니다. 이번에는 이런 아이디어를 생각해봅니다.

[MIN, MAX] 의 범위에서 해당 수가 몇 개 저장되어 있는지를 따져보자

즉, 해당 문제에서 나올 수 있는 값의 범위가 [0, 65536]이므로 이것에 대한 세그먼트 트리를 만드는 것입니다.

update

update(int node, int s, int e, int idx, int val) 에서

• idx : 우리가 트리에 삽입할 수 그 자체가 됩니다. 즉, 이는 [0, 65536]를 가집니다.
• val : 값을 추가할 때는 1, 삭제할 때는 -1을 가집니다. tree에는 해당 노드에 해당하는 범위를 만족하는 수의 갯수가 저장됩니다.

작동 과정을 보도록 하겠습니다. 편의상 MIN = 1, MAX = 5 로 두겠습니다.

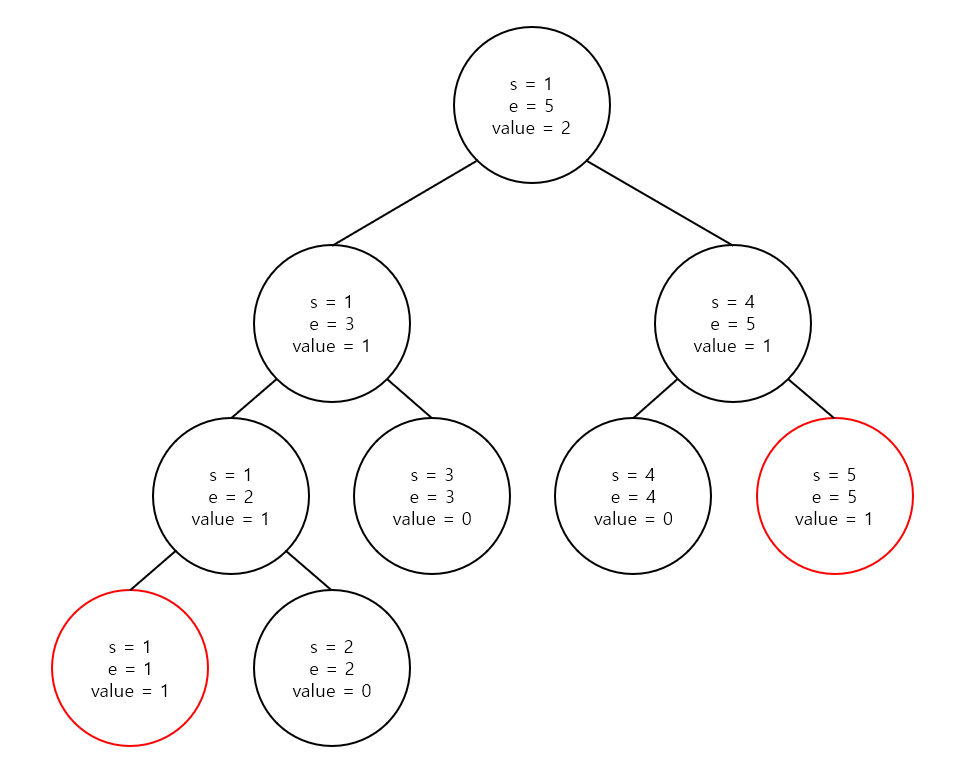
그림 상으로는 1과 5가 들어있는 세그먼트 트리를 나타낸 것입니다. 편의상 1과 5가 들어있다는 것을 표시하는 노드를 빨간색으로 두었습니다.

여기에 3을 넣어보겠습니다. update(1, 1, 5, 3, 1) 을 실행합니다.
그러면 아래와 같은 파란색 경로를 따라갑니다.

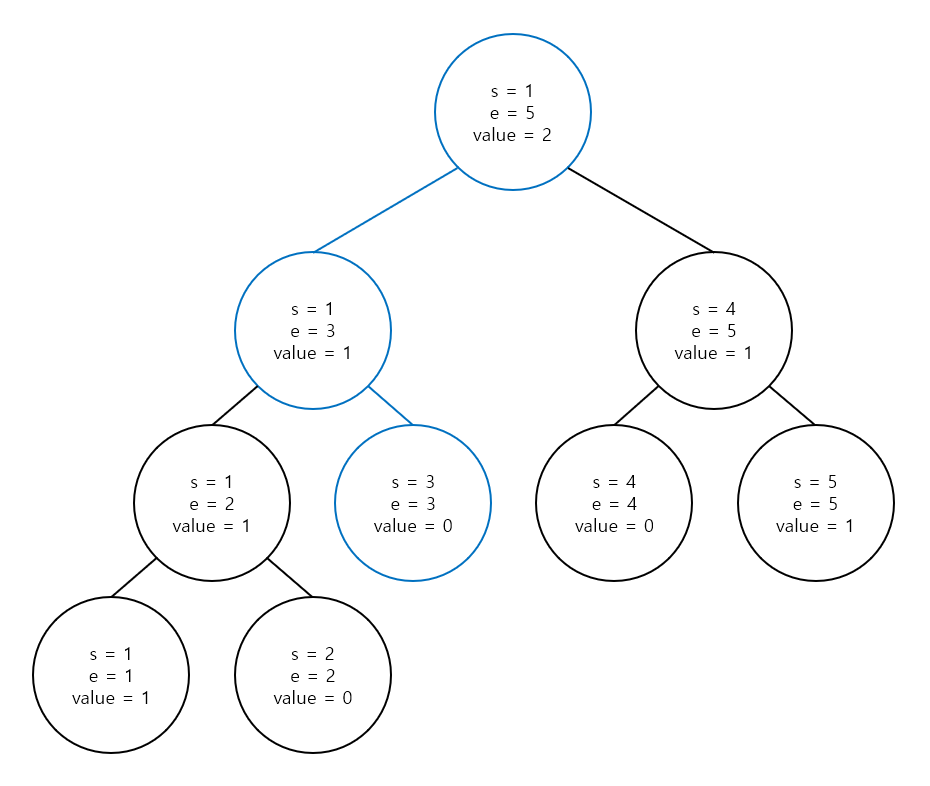
그리고 지나간 모든 노드에 val만큼 더해줍니다.

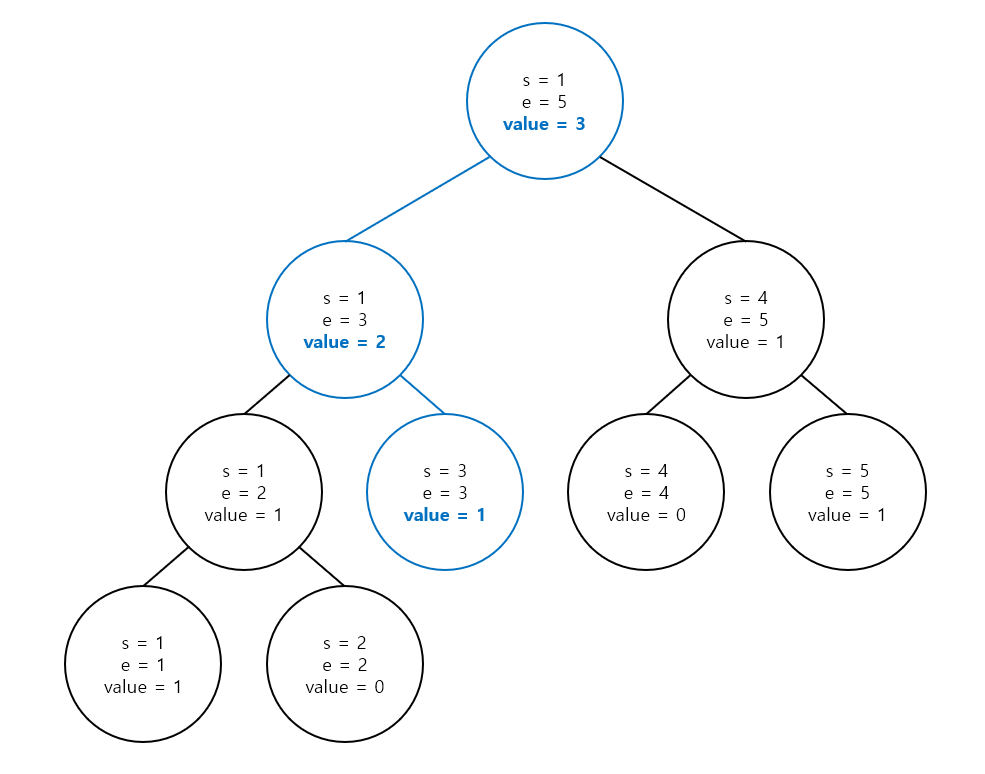
즉, tree가 갱신되면서 각 노드에 들어가있는 값은 사실 하위 노드에 저장된 수의 갯수가 되는 사실을 다시 한번 볼 수 있습니다.

삭제도 간단하게 보겠습니다. 현 상태에서 1을 지워보겠습니다.
update(1, 1, 5, 1, -1) 을 실행합니다.

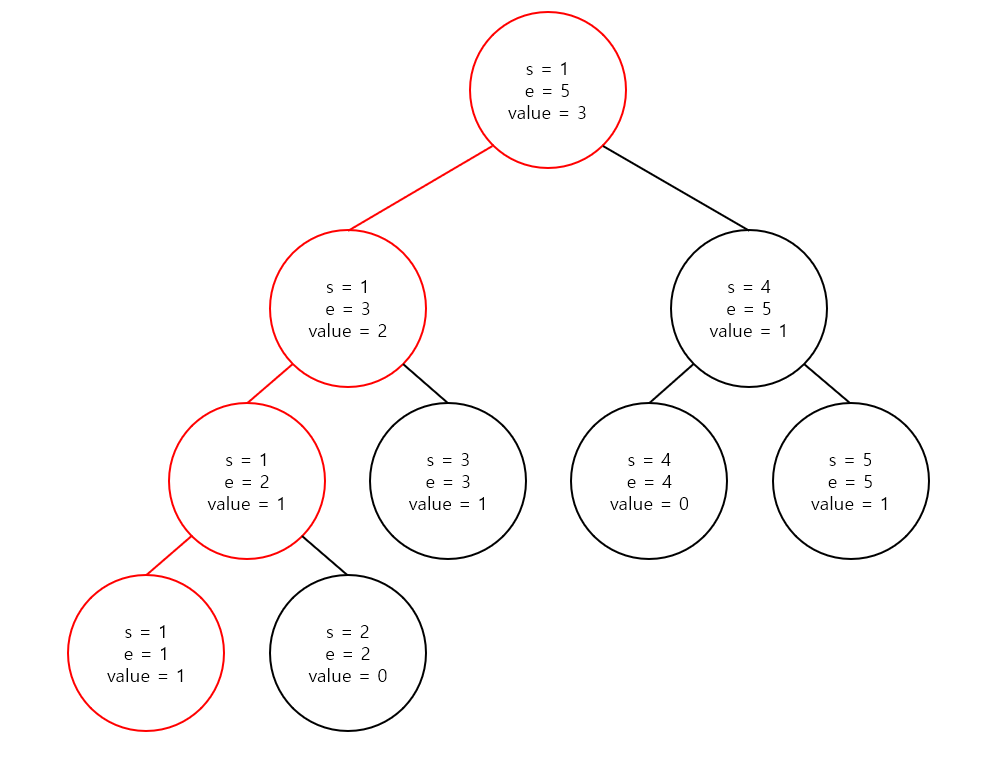
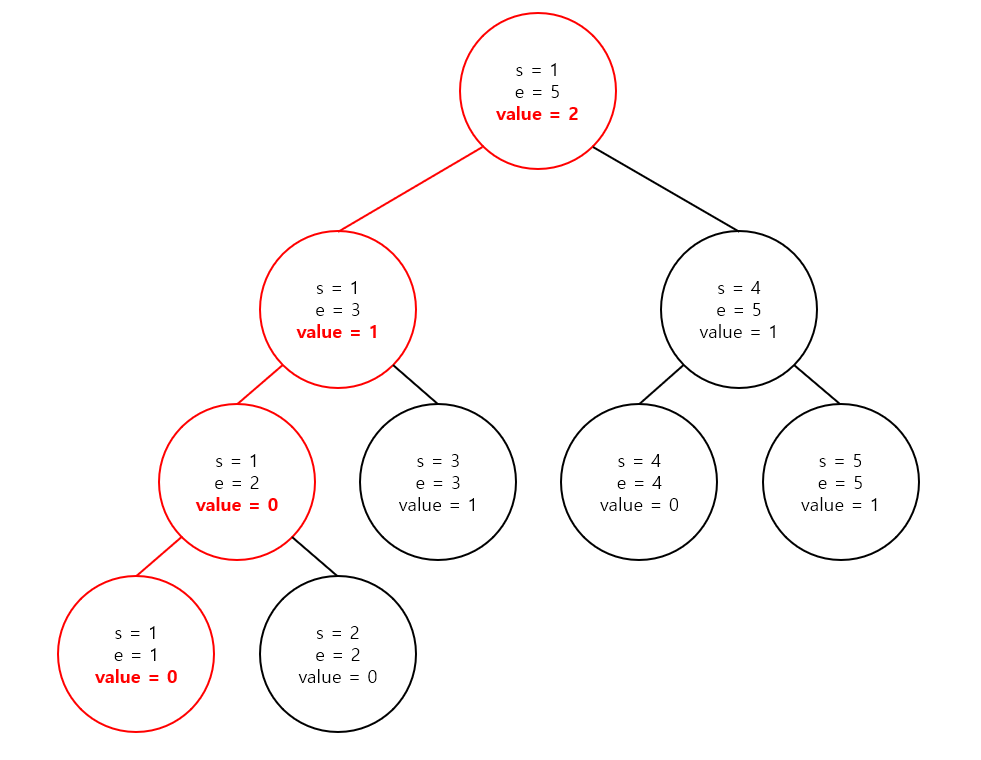
삭제는 반대로 1을 빼주면, 즉 -1을 더하면 노드 값이 1 감소하면서 저장된 수의 갯수가 갱신되는 것을 확인할 수 있습니다.

구현은 과연 어떨까요? 사실 구현은 기존 세그먼트 트리에서 val에 들어가는 값이 1, -1만 다르기 때문에 달라진 것이 없습니다. 그래도 한번 작성하고 가겠습니다.

    static void update(int node, int s, int e, int idx, int val) {
        if(idx < s || e < idx) return;
        if(s == e) {
            tree[node] += val;
            return;
        }
        int mid = (s + e) / 2;
        update(2 * node, s, mid, idx, val);
        update(2 * node + 1, mid + 1, e, idx, val);
        tree[node] = tree[2 * node] + tree[2 * node + 1];
    }

get

본격적으로 구현이 달라지는 get입니다. 이 부분은 누적합이 아닌 실제 우리가 원하는 순서의 숫자를 뽑아야합니다. 편의상 k번째 숫자를 얻는다고 하겠습니다.

생각해보면 이미 트리라 생각하지 말고 이미 k번째 숫자를 빠르게 얻는 방법을 알고 있습니다. 바로 이진 탐색(binary search) 입니다. 이를 세그먼트 트리에 적용해봅니다.

아이디어

간단한 아이디어에서 출발합니다. 바로 tree[node]는 해당 범위에서 저장 된 수의 갯수를 의미한다는 것입니다. 그리고 자식으로는 작은 범위의 수 갯수에 해당하는 tree[2 * node] 와 큰 범위인 tree[2 * node + 1]를 사용합니다.

이 때, k가 tree[2 * node]보다 크다면 어떨까요? 우리는 최소한 찾는 수가 tree[2 * node]가 가리키는 범위보다는 큰 범위에 있음을 알 수 있습니다. 따라서 tree[2 * node + 1]을 탐색해줍니다.

반대는 어떨까요? 쉽게 알 수 있지만 tree[2 * node]에 있음을 알 수 있습니다.

즉 다음과 같습니다.

1. k > tree[2 * node] : tree[2 * node + 1] 탐색
2. k <= tree[2 * node] : tree[2 * node] 탐색

단 주의할 점이 있습니다. 바로 첫번째 경우인데, 만약에 tree[2 * node + 1]를 탐색한다고 하면 그 이후에도 k를 기준으로 해야될까요?

아닙니다. 바로 탐색할 범위가 줄어듭니다. 왼쪽 노드를 더 탐색할 필요가 없고, 오른쪽 노드부터 새로운 시작을 해서 탐색해야됩니다.

예를 들어 k = 3 이고, 왼쪽은 2, 오른쪽은 2라면 오른쪽을 탐색해야되는데, k가 변경이 되지 않는다면 오른쪽에 대해 크기는 2인 노드에 대해 3번째 노드를 찾으라는 말도 안되는 쿼리가 떨어지게 됩니다.

즉, tree[2 * node + 1]를 탐색한다고 하면 k := k - tree[2 * node] 로 변경해주어야 합니다. 이를 코드로 구현하면 다음과 같습니다.

    static int get(int node, int s, int e, int val, int kth) {
        if(s == e) return s;
        int mid = (s + e) / 2;
        int left = tree[2 * node];
        if(kth <= left) {
            return get(2 * node, s, mid, val, kth);
        } else {
            return get(2 * node + 1, mid + 1, e, val, kth - left);
        }
    }

BOJ 1572 소스코드

해당 문제는 다음과 같은 과정을 거치면 됩니다.

• 해당 순번 숫자를 추가해줍니다. (update, val = 1)
• (K + 1) / 2번째 수를 찾고 이를 결과에 더해줍니다. (get)
• 해당 순번 - (K - 1) 번째 숫자를 빼줍니다.(update, val = -1)

import java.io.*;
import java.util.*;

public class Main {
    static int N, K;
    static int[] arr, tree;
    static final int MAX = 65536;
    static void init() {
        int size = 1 << ((int) Math.ceil(Math.log(MAX + 1) / Math.log(2)) + 1);
        arr = new int[N];
        tree = new int[size];
    }
    static int get(int node, int s, int e, int val, int kth) {
        if(s == e) return s;
        int mid = (s + e) / 2;
        int left = tree[2 * node];
        if(kth <= left) {
            return get(2 * node, s, mid, val, kth);
        } else {
            return get(2 * node + 1, mid + 1, e, val, kth - left);
        }
    }
    static void update(int node, int s, int e, int idx, int val) {
        if(idx < s || e < idx) return;
        if(s == e) {
            tree[node] += val;
            return;
        }
        int mid = (s + e) / 2;
        update(2 * node, s, mid, idx, val);
        update(2 * node + 1, mid + 1, e, idx, val);
        tree[node] = tree[2 * node] + tree[2 * node + 1];
    }
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = null;
        st = new StringTokenizer(br.readLine(), " ");
        N = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());
        init();
        long answer = 0;
        for(int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(br.readLine());
        }
        for(int i = 0; i < K - 1; i++) {
            update(1, 0, MAX, arr[i], 1);
        }
        for(int i = K - 1; i < N; i++) {
            update(1, 0, MAX, arr[i], 1);
            answer += get(1, 0, MAX, val, (K + 1) / 2);
            update(1, 0, MAX, arr[i - K + 1], -1);
        }
        System.out.println(answer);
        br.close();
    }
}