그래프
정점Vertex와 간선Edge의 집합입니다. 그래프는 G=(V,E)로 정의되요.
여기서 V는 공백이 아닌 노드Node 혹은 정점Vertex의 유한 집합으로 정점만을 표현할 땐 V(G)라고 표기해요.
E는 서로 다른 두 정점Vertex를 잇는 간선Edge의 유한 집합이고 간선만 표현할 때는 E(G)라고 표기해요.
위에서 노드Node가 언급되었는데, 이는 트리에서도 사용되는 용어죠. 이 말은 트리Tree도 그래프의 일부 중 하나입니다.
방향/무방향 그래프
방향 그래프
간선에 방향이 있는 그래프에요. 모든 간선에 순서가 존재해, V0, V1라는 정점을 간선으로 이었을 때, V0 V1와 V0 V1이 따로 존재합니다.
이때 V0 V1를 <V0, V1>, 반대는 <V1, V0>이라 표기해요.
무방향 그래프
간선에 방향이 없는 그래프에요. V0, V1라는 정점을 간선으로 이었을 때, 간선 (V0, V1), (V1, V0)는 똑같은 간선을 나타내요.
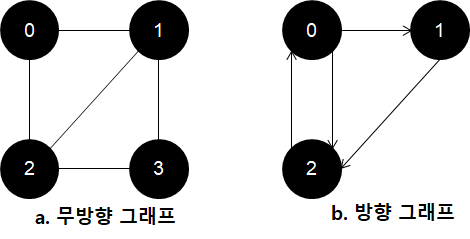
V(a) = {0, 1, 2, 3}, E(a) = { (0, 1), (0, 2), (1, 2), (1, 3), (2, 3) }
V(b) = {0, 1, 2}, E(b) = { <0, 1>, <0, 2>, <1, 2>, <2, 0> }
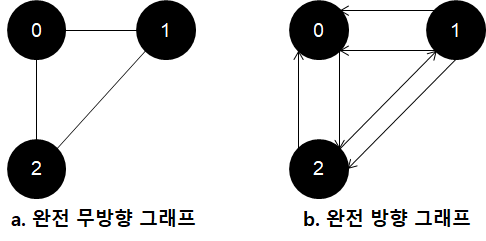
완전 그래프(Complete Graph)
간선을 최대한으로 가진 그래프를 말합니다.
n개의 정점을 가진 무방향 그래프의 최대 간선 수는 개입니다.
그리고 n개의 정점을 가진 방향 그래프의 최대 간선 수는 개입니다. 방향인 경우, 무방향에 비해 2배 늘어난다고 생각하시면 될 듯합니다.
부분 그래프(Sub-graph)
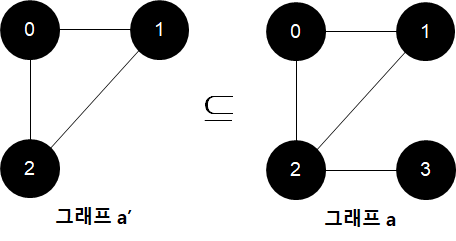
그래프 a가 주어졌을 때 정점 V(a') V(a)이고, E(a') E(a)일 때 그래프 a'는 그래프 a의 부분 그래프라고 해요. 아래를 보시고 이해하시면 됩니다.
인접(Adjacent) & 부속(Incident)
무방향 그래프에서 나오는 개념입니다.
인접
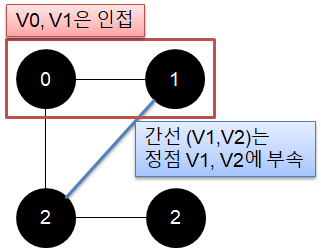
간선 (V0,V1)가 무방향 그래프 G의 간선일 때 정점 V0, V1는 서로 인접한다고 해요.
부속
간선 (V0, V1)가 무방향 그래프 G의 간선일 때 간선 (V0, V1)는 정점 V0, V1의 부속이 된다고 해요.
경로(Path)
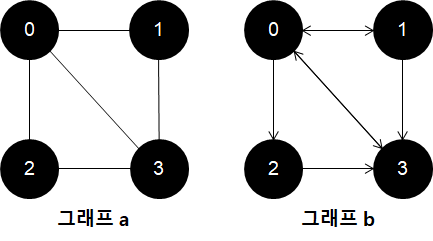
아래 그림의 그래프 a와 같이 정점 V0부터 V3까지의 간선으로 연결된 정점의 순서 리스트V0, V1, V2, V3를 경로라 합니다.
그리고 그래프 b같은 방향 그래프의 경우 방향 경로라고 해요.

단순 경로
모두 상이한 간선으로 구성된 경로에요. 그래프 b에선 V0, V1, V2는 단순 경로지만, V0, V1, V0, V1, V2는 단순 경로가 아닙니다.
사이클(Cycle)
첫 번째 정점Vertex와 마지막 정점이 동일한 단순 경로를 의이합니다.
그래서 무방향 그래프에선 사이클의 길이 3이고, 방향 그래프에선 사이클의 길이 2입니다.
여기서 사이클이 존재하지 않는 그래프는 Directed Acyclic GraphDAG라고 합니다.
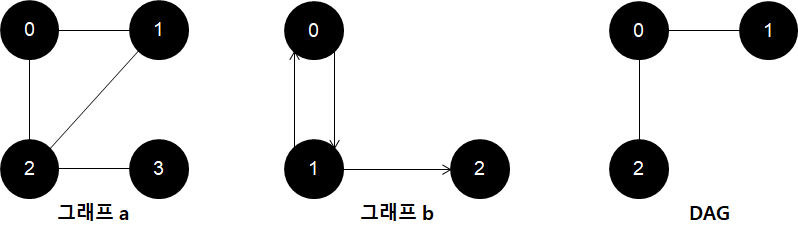
아래 그림을 보자면 그래프 a는 정점 V0, V1, V2, V0이 사이클이며, 그래프 b는 정점 V0, V1이 사이클입니다.
강한 연결 & 약한 연결
방향 그래프에서 나오는 개념이에요.
강한 연결
방향 그래프 G에서 V(G)에 있는 서로 다른 모든 정점의 쌍 u와 v에 대해, u v 그리고 v u에 대한 방향 경로가 있을 때를 의미합니다.
약한 연결
강한 연결과 달리 둘 중 하나만 있는 경우를 말합니다.
아래 그림을 보시면 그래프 a는 모든 정점이 양방향으로 경로가 있어 강한 연결이고, 그래프 b는 간선 <1,3>로 인해 V1 V0은 되지만 V0 V1는 연결되지 않아 약한 연결입니다.

차수(Degree)
정점의 차수Degree of Vertex는 그래프에서 그 정점에 부속된 간선의 수를 말해요.
진입 차수(In-degree) & 진출 차수(Out-degree)
방향 그래프에서 나오는 개념으로, 정점 V의 진입 차수In-degree는 정점 V를 head로 하는 간선의 수를 말하고, 진출 차수Out-degree는 정점 V를 tail로 하는 간선의 수를 의미해요.
아래 그림 기준, 그래프 a의 정점 V0의 차수는 3이고, 그래프 b의 정점 V0의 진입 차수는 2, 진출 차수는 3입니다.