
지난번에 이진 트리와 그 종류에 대해서 다뤄봤어요. 개념을 알았으니 활용할줄 알아야죠.
이를 활용한 힙 트리 Heap Tree에 대해서 다뤄보겠습니다.
힙 트리란?
배열의 원소를 정렬하기 위한 구조라고 보시면 됩니다. 우선순위 큐Priority Queue를 구현하는데 있어 핵심적인 개념입니다.
우선순위 큐는 큐Queue와 동일하게 가장 앞에 있는 것을 빼올 수 있는 자료구조인데, 우선순위가 가장 높은(오름차순인 경우 가장 작은 수)를 먼저 빼오게 됩니다.
이것을 가능하게 하려면 큐의 배열을 힙 트리로 구성해야 합니다. 먼저 힙에 대해 설명드리자면,
- 완전 이진 트리
CBT- 반정도 정렬된 상태, 노드의 부모는 자식들보다 우선순위가 높아야 합니다.
힙 종류
크게 두 가지로 나뉘고 최대 힙Max Heap과 최소 힙Min Heap으로 나뉩니다.
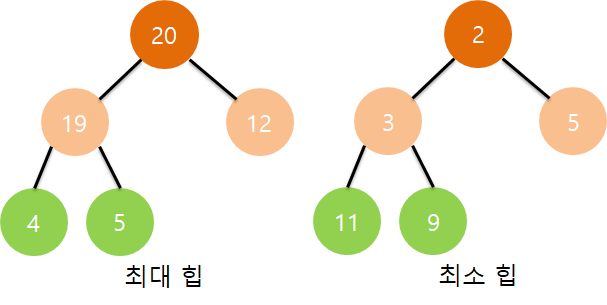
최대 힙
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
최소 힙
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
구현
힙을 저장하는 표준적인 자료구조는 배열Array이에요.
노드 관계
0-base
왼쪽 자식 : (부모 index) x 2 + 1
오른쪽 자식 : (부모 index) x 2 + 2
부모 : (자식 index) / 2 - 1
구현을 편하게 하기 위해 0 번째 배열을 사용하지 않기도 합니다. 그렇게 되면 관계는 아래와 같아요.
1-base
왼쪽 자식 : (부모 index) x 2
오른쪽 자식 : (부모 index) x 2 + 1
부모 : (자식 index) / 2
삽입
- 힙에 새로운 요소가 들어오면 새로운 노드를 마지막에 삽입합니다.
- 새로운 노드와 부모 노드를 우선순위 비교하여 교환하며 타고 올라갑니다.
대표적인 정렬 로직 중 하나인 힙 소트Heap Sort는 최대 힙을 활용해 정렬합니다. 그래서 내림차순으로 로직을 작성하겠습니다.
참고로 0-base에요.
void insert(T x)
{
m_heap[m_heapSize] = x;
for(int i = m_heapSize; i > 0; i /= 2)
{
if(m_heap[i] > m_heap[i / 2])
{
swap(m_heap[i], m_heap[i / 2]);
}
else
{
break;
}
}
++m_heapSize;
}삭제
- 힙(여기선 최대 힙)에서 최대 값은 루트 노드이므로 루트 노드를 삭제합니다(뭔가 결과를 보고 싶다면 삭제하기 전에 변수에 저장해서 반환해야겠죠?).
- 삭제된 루트 노드에 마지막 노드를 가져옵니다.
- 힙을 재구성합니다.
T pop()
{
T ret = m_heap[0];
m_heap[0] = m_heap[m_heapSize];
for(int i = 0; i * 2 < m_heapSize;)
{
// 두 자식들보다 큰 경우
if(m_heap[i] > m_heap[i * 2 + 1] && m_heap[i] > m_heap[i * 2 + 2])
break;
// 좌측이 더 큰 경우
else if(m_heap[i * 2 + 1] >= m_heap[i * 2 + 2])
{
swap(m_heap[i], m_heap[i * 2 + 1]);
i = i * 2 + 1;
}
// 우측이 더 큰 경우
else
{
swap(m_heap[i], m_heap[i * 2 + 2]);
i = i * 2 + 2;
}
}
--m_heapSize;
return ret;
}Heapify
힙을 구성하는데 통상적으로 쓰이는 메서드 이름으로 기준 인덱스를 매개변수로 받아와 해당 시점부터 힙을 구성하는 로직이라 보시면 됩니다.
n 변수가 있는데, 해당 인덱스 - 1까지만 구성한다고 보시면 됩니다. 이렇게 로직을 전개한 이유는 힙 정렬에서 응용할 수 있기 때문이에요.
힙 정렬의 기본 로직은,
- 배열을 최대 힙으로 구성합니다.
- 최대 힙의 루트 노드와 마지막 노드를 바꿉니다.
2-1. 이로서 마지막 값은 정렬이 된 것을 알 수가 있습니다.
2-2. 따라서, 정렬된 노드를 제외하여 힙을 구성하고 1, 2를 반복하면 정렬된 배열을 구할 수 있죠.
Heapify, Heapify로 구성한 Insert와 Pop은 아래와 같아요.
void insertByHeapify(T x)
{
m_heap[m_heapSize++] = x;
for(int i = m_heapSize / 2 - 1; i >= 0; --i){
heapify(m_heapSize, i);
}
}
T popByHeapify()
{
T ret = m_heap[0];
m_heap[0] = m_heap[m_heapSize - 1];
m_heap[m_heapSize--] = 0;
heapify(m_heapSize, 0);
return ret;
}
void heapify(int n, int i)
{
int parent = i;
int lChild = i * 2 + 1;
int rChild = i * 2 + 2;
if(lChild < n && m_heap[parent] < m_heap[lChild])
parent = lChild;
if(rChild < n && m_heap[parent] < m_heap[rChild])
parent = rChild;
if(i != parent)
{
swap(m_heap[parent], m_heap[i]);
heapify(n, parent);
}
}
사용 예제는 아래를 참고하시면 됩니다.
