[자료구조] 이진 탐색 트리(Binary Search Tree) (삽입, 검색, 삭제 편)

최지수·2021년 11월 21일

computer science data structure

자료구조

목록 보기

4/7

이전에 이진 트리Binary Tree를 활용하면 탐색을 효율적으로 할 수 있다고 했습니다. 어떻게 이게 가능한지, 그리고 관리를 어떻게 하는지에 대해 설명 드리겠습니다.

이진 탐색 트리

이진 탐색binary search과 연결리스트linked list를 결합한 자료구조의 일종입니다

두개의 자식 노드를 가졌으며(하나를 left, 하나를 right라 칭하면), 현재 노드의 left 노드의 값은 현재보다 작으며, right 노드의 값은 현재보다 크도록 구성하는 트리입니다.

삽입

삽입하려는 값과 노드 내 값을 비교하면서 작으면 좌측 노드로, 크면 우측 노드로 타고 내려가면서 배치하는 방식을 전개해요.

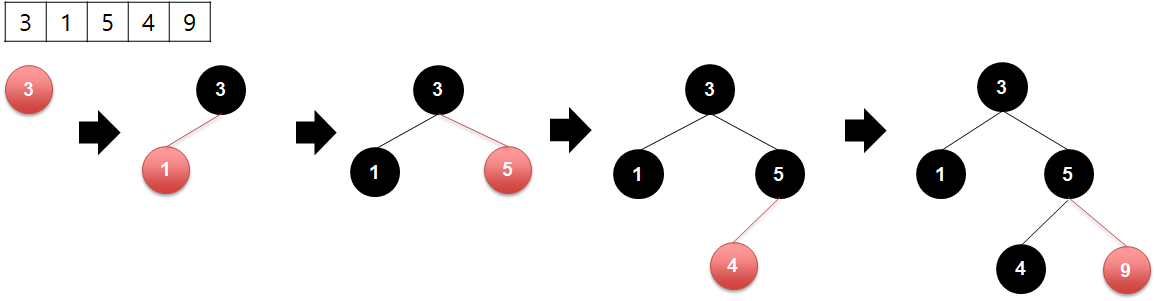
이렇게 트리가 left는 부모보다 작고, right는 부모보다 크게 구성이 되도록 해야 합니다.

코드

public void add(int value){
    if(rootNode == null){
        rootNode = new DoubleLinkedList();
        rootNode.setValue(value);
        return;
    }

    if(rootNode.getValue() >= value){
        if(null != rootNode.getLeftNode()) {
            add(rootNode.getLeftNode(), value);
        }
        else{
            rootNode.setLeftNode(new DoubleLinkedList());
            rootNode.getLeftNode().setParentNode(rootNode);
            rootNode.getLeftNode().setValue(value);
        }
    }else{
        if(null != rootNode.getRightNode()) {
            add(rootNode.getRightNode(), value);
        }
        else{
            rootNode.setRightNode(new DoubleLinkedList());
            rootNode.getRightNode().setParentNode(rootNode);
            rootNode.getRightNode().setValue(value);
        }
    }
}

private void add(DoubleLinkedList node, int value){
    if(null == node)
        return;

    if(node.getValue() >= value){
        if(null != node.getLeftNode()) {
            add(node.getLeftNode(), value);
        }
        else{
            node.setLeftNode(new DoubleLinkedList());
            node.getLeftNode().setParentNode(node);
            node.getLeftNode().setValue(value);
        }
    }else{
        if(null != node.getRightNode()) {
            add(node.getRightNode(), value);
        }
        else{
            node.setRightNode(new DoubleLinkedList());
            node.getRightNode().setParentNode(node);
            node.getRightNode().setValue(value);
        }
    }
}

검색

마지막으로 구성된 트리에서 4를 찾을 때입니다.

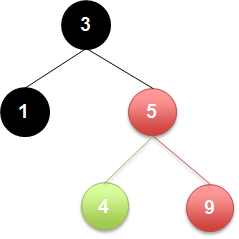
처음 트리에 진입을 하면 3을 보게 됩니다. 그리고 4는 3보다 크므로 left 노드를 볼 필요가 없어요. 그리고 5의 노드에선 4가 5보다 작으므로 left 노드를 찾아 들어가면 5 노드의 right는 볼 필요도 없어지죠.

이렇게 되면 순회하며 검색( $O(n)$ )보다, 한번 검색을 할 때마다 검색 범위가 절반으로 줄어들기 때문에, 노드의 개수가 $2^{k(트리의 높이)}$ 라 가정할 때 한번 집입할 때마다 높이를 빼고 내려가므로 높이 개수k만큼만 검색을 수행하므로 $k = log_{2}n \cong O(logn)$ 의 속도를 기대할 수 있습니다. 훨씬 빨라졌죠.

코드

private DoubleLinkedList findNode(int value){
    if(rootNode.getValue() == value)
        return rootNode;

    DoubleLinkedList node = null;
    if(rootNode.getValue() > value){
        node = findNode(rootNode.getLeftNode(), value);
    }
    else if(rootNode.getValue() < value){
        node = findNode(rootNode.getRightNode(), value);
    }

    return node;
}
private DoubleLinkedList findNode(DoubleLinkedList node, int value){
    if(null == node)
        return null;

    DoubleLinkedList node2 = null;
    if(node.getValue() > value){
        node2 = findNode(node.getLeftNode(), value);
    }
    else if(node.getValue() < value){
        node2 = findNode(node.getRightNode(), value);
    }
    else{
        node2 = node;
    }
    return node2;
}

삭제

삭제Delete의 경우, 3가지 전제 조건을 가지고 처리해야 합니다.

삭제하려는 노드(이하 삭제 노드)의 자식 개수 0

삭제 노드의 자식 개수 1개

삭제 노드의 자식 개수 2개

모든 예시를 다룰 수 있게 아래와 같은 트리를 구성해보죠.

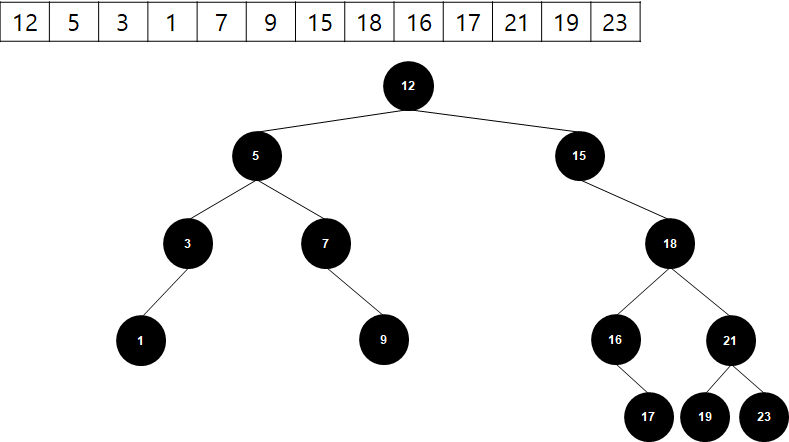
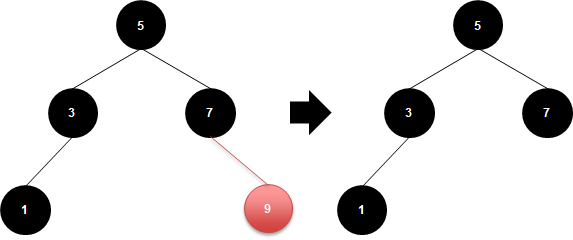
삭제 노드의 자식 개수 0개

이 경우는 간단해요. 그냥 삭제 노드만 연결을 끊어주면 됩니다.

삭제 노드의 자식 개수 1개

15를 삭제한다고 가정해볼게요. 자식 노드가 right에 1개 있네요.

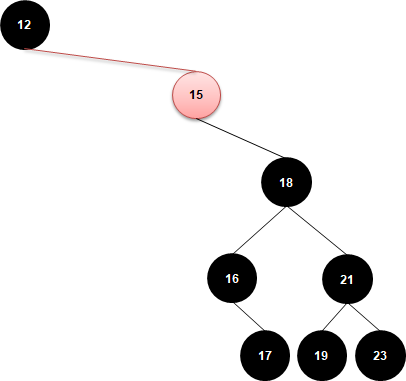
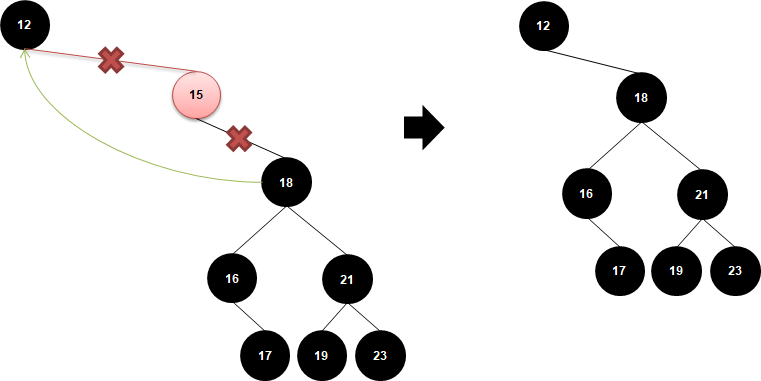
이 경우엔 부모 노드인 12가 삭제 노드의 right 자식인 18을 참조하면 됩니다. 예제에서는 right가 있지만 left에만 있다면 해당 자식 노드를 참조하면 되겠죠?

삭제 노드의 자식 개수 2개

이 경우가 조금 복잡합니다. 우선 삭제 노드에 위치하려는 노드를 먼저 정해야 합니다.

위치하려는 노드(기준 노드라 할게요)
1. 삭제 노드의 left에 있는 노드 중 제일 큰 노드
2. 삭제 노드의 right에 있는 노드 중 제일 작은 노드

일반적으로 2번을 기준 노드로 잡는다고 하네요. 그래서 2번을 기준으로 말씀드릴게요.

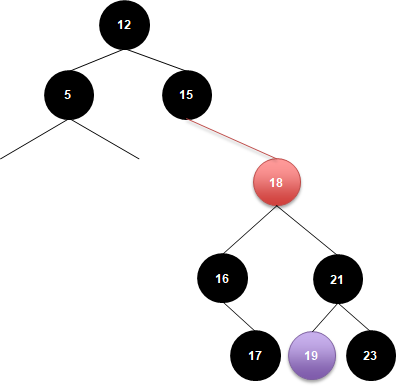
18 노드를 삭제하려면 해당 노드의 기준 노드는 19 노드가 됩니다. 그러면 삭제 노드의 값을 15로 바꿔주면 이진 검색 트리의 규칙을 유지한 채로 삭제를 수행할 수 있게 됩니다!

여기서 만약 기준 노드19에 right 노드가 존재한다면 기준 노드 기준 최우측에 삭제 노드의 right 노드인 21 노드를 배치하면 됩니다.

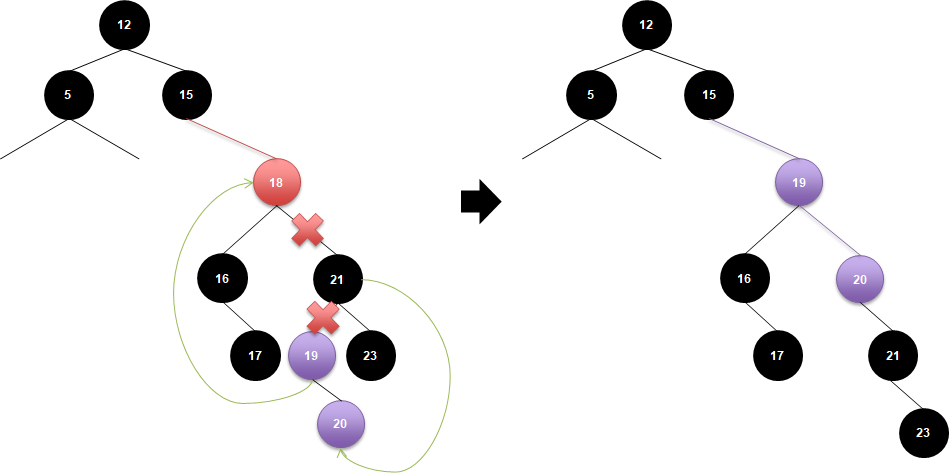
~~이렇게 보니까 기준 노드의 위치에 기준 노드의 right 노드를 배치시켜줘도 되긴 하네요 ㅎㅎ~~

삭제 로직을 정리하자면,

이진 탐색 트리 요소 삭제
1. 삭제 노드에 위치할 노드를 정한다
1-1. 삭제 노드 기준 left 노드 내 가장 큰 노드
1-2. 삭제 노드 기준 right 노드 내 가장 큰 노드 -> 일반적으로 2번을 주로 사용
2. 해당 기준 노드를 삭제 노드에 위치시킨다.
2-1. (2번으로 기준 노드 지정) 기준 노드의 가장 끝에 있는 right 노드에 삭제 노드의 right 노드 위치

코드


public void delete(int value){
    DoubleLinkedList deleteNode = findNode(value);
    if(null == deleteNode)
        return;

    // 1. 자식이 없음
    if(deleteNode.getLeftNode() == null && deleteNode.getRightNode() == null){
        if(deleteNode == rootNode){
            rootNode = null;
            return;
        }

        var parentNode = deleteNode.getParentNode();
        if(deleteNode == parentNode.getLeftNode())
            parentNode.setLeftNode(null);
        else if(deleteNode == parentNode.getRightNode())
            parentNode.setRightNode(null);
        deleteNode.setParentNode(null);
    }
    // 2-1. 좌측에만 존재
    else if(deleteNode.getLeftNode() != null && deleteNode.getRightNode() == null){
        var leftNode= deleteNode.getLeftNode();
        if(deleteNode == rootNode){
            rootNode = leftNode;
        }else{
            var parentNode = deleteNode.getParentNode();
            if(deleteNode == parentNode.getLeftNode()){
                parentNode.setLeftNode(leftNode);

            }
            else if(deleteNode == parentNode.getRightNode()){
                parentNode.setRightNode(leftNode);
            }

            deleteNode.setParentNode(null);
            deleteNode.setLeftNode(null);
            deleteNode.setRightNode(null);
        }
    }
    // 2-2. 우측에만 존재
    else if(deleteNode.getLeftNode() == null && deleteNode.getRightNode() != null){
        var rightNode= deleteNode.getRightNode();
        if(deleteNode == rootNode){
            rootNode = deleteNode.getRightNode();
        }else{
            var parentNode = deleteNode.getParentNode();
            if(deleteNode == parentNode.getLeftNode()){
                parentNode.setLeftNode(rightNode);

            }
            else if(deleteNode == parentNode.getRightNode()){
                parentNode.setRightNode(rightNode);
            }

            deleteNode.setParentNode(null);
            deleteNode.setLeftNode(null);
            deleteNode.setRightNode(null);
        }
    }
    // 3. 자식이 두개 존재
    else{
        // 1. 기준 노드 -> 삭제 노드의 우측 자식 중 가장 작은 노드
        var minNode = deleteNode.getRightNode();
        while(null != minNode.getLeftNode())
            minNode = minNode.getLeftNode();

        if(null == minNode)
            return;

        // 2-1. 기준 노드 좌측에 삭제 노드의 좌측 노드 배치
        if(deleteNode.getLeftNode() != minNode){
            minNode.setLeftNode(deleteNode.getLeftNode());
        }
        // 2-2. 기준 노드 우측에 삭제 노드의 '최'우측 노드 배치
        if(deleteNode.getRightNode() != minNode){
            var minestNode = minNode;
            while(null != minestNode.getRightNode())
                minestNode = minestNode.getRightNode();
            minestNode.setRightNode(deleteNode.getRightNode());
            // 삭제 노드 좌측 노드 삭제
            deleteNode.getRightNode().setLeftNode(null);
        }
        // 2-3. 기준 노드를 삭제 노드 위치에 배치(삭제 노드의 부모 위치)
        if(null != deleteNode.getParentNode()){
            var parentNode = deleteNode.getParentNode();
            if(deleteNode == parentNode.getLeftNode()){
                parentNode.setLeftNode(minNode);
            }
            else if(deleteNode == parentNode.getRightNode()){
                parentNode.setRightNode(minNode);
            }
        }

        deleteNode.setParentNode(null);
        deleteNode.setLeftNode(null);
        deleteNode.setRightNode(null);
    }

}

private DoubleLinkedList findNode(int value){
    if(rootNode.getValue() == value)
        return rootNode;

    DoubleLinkedList node = null;
    if(rootNode.getValue() > value){
        node = findNode(rootNode.getLeftNode(), value);
    }
    else if(rootNode.getValue() < value){
        node = findNode(rootNode.getRightNode(), value);
    }

    return node;
}
private DoubleLinkedList findNode(DoubleLinkedList node, int value){
    if(null == node)
        return null;

    DoubleLinkedList node2 = null;
    if(node.getValue() > value){
        node2 = findNode(node.getLeftNode(), value);
    }
    else if(node.getValue() < value){
        node2 = findNode(node.getRightNode(), value);
    }
    else{
        node2 = node;
    }
    return node2;
}