
이진 탐색 트리Binary Search Tree는 트리 구조로 원소를 저장하여 의 검색 속도를 보여줍니다. 하지만 원소가 정렬된 상태로 들어오게 되면 의 속도를 보이게 되요. 원소의 개수와 트리의 높이가 동일하기 때문이죠.
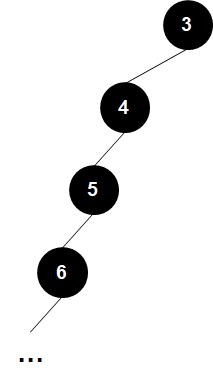
Red-black Tree
이를 개선하기 위해 나온 개념이 바로 Red-black Tree에요적흑 트리라고 하던데 일반적으로 영어로 이야기를 해요.
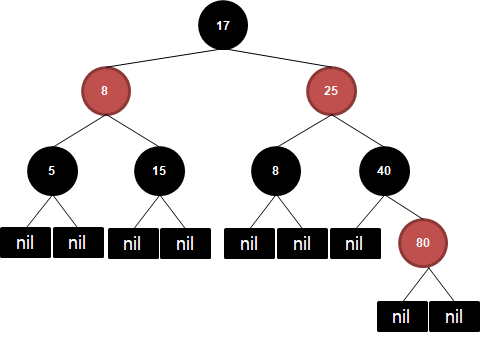
이렇게 각 노드에 색을 저장하는 공간을 추가해, 이를 기준으로 균형 이진 트리Balanced Binary Tree를 구성하는 트리입니다.
구성요소와 규칙
Red-black Tree는 노드에 red와 black 색상을 추가로 가지고 있으며, 마지막 leaf 노드는 nil이라는 black색의 빈 노드로 구성되요. nil의 경우 하나의 노드로 관리해서 메모리를 절약할 수도 있어요.
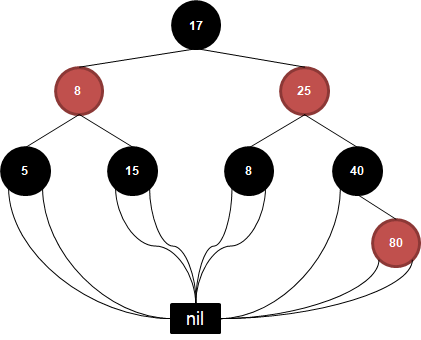
그리고 아래와 같은 규칙을 통해 균형을 맞춥니다.
Red-black Tree 규칙
1. Root Property : 루트Root노드는black
2. External Property : 모든 리프leaf노드는black
3. Internal Property :red노드의 자식 노드는 항상blackDouble Red 불가!
4. Depth Property : 각 노드로부터 해당 노드의 리프leaf로 가는 경로는 모두black개수가 일치
전략
루트 노드를 제외하고 모든 노드는 추가될 때마다 red 색상으로 초기화된 상태로 추가가 됩니다. 그러다보면 3번 규칙이 위배가 됩니다.
Red-black Tree에선 이를 해결하기 위해 2가지 조건을 가지고 전략을 취합니다.
Double Red 해결 전략
1. Recoloring :
- 조건 : 삽입된 노드의 부모와 부모의 형제(삼촌이라 할게요) 노드가 서로 같을 경우(둘 다
red),- 전략 : 부모와 삼촌 노드를
black으로, 부모의 부모 노드를red로 바꿔줍니다.
- Restructuring
- 조건 : 삽입된 노드의 부모와 부모의 형제(삼촌이라 할게요) 노드가 서로 다를 경우
- 전략 : 삽입, 부모, 부모의 부모 노드를 오름차순 정렬, 중간 노드를 부모로 하고
black을, 나머지를 자식으로 하고red로 바꿔줍니다.
예제
자, 앞서 말씀드린 규칙과 전략을 복기하면서 천천히 전개해봅시다. 원소 [8, 18, 5, 15, 17, 25, 40, 80]가 주어졌을 때의 트리를 구성해보겠습니다.
Step 1 : 8

루트 노드는 추가할 때 black으로 초기화해요.
Step 2 : 18

다음은 무조건 red로 초기화됩니다.
Step 3 : 5
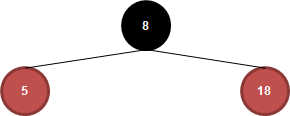
Step 4 : 15
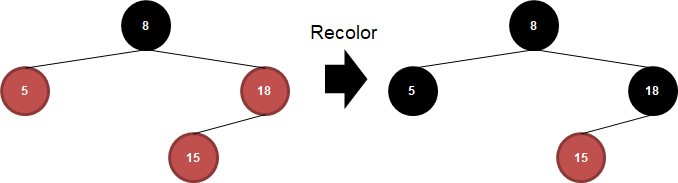
15가 추가되면서 Double Red가 발생했습니다. 이 경우 부모와 삼촌 노드가 색이 같으므로 Recoloring 전략을 써서 부모와 삼촌 노드 색을 black으로 바꿔줍니다.
원래 부모의 부모 노드 색도 red로 바꿔줘야 하나, 루트 노드는 항상 black이므로, 색을 변경해주지 않습니다.
Step 5 : 17
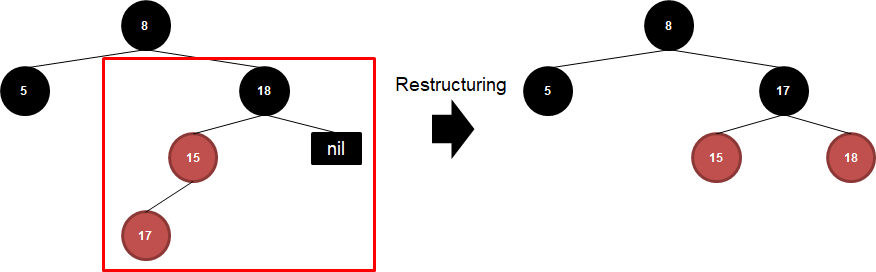
17이 추가되면서 Double Red가 발생했습니다. 이 경우, 부모와 삼촌 노드 색이 서로 다르므로(nil은 항상 black),
Restructuring 전략을 써서 삽입, 부모, 부모의 부모 노드를 오름차순 정렬, 중간 노드를 부모로 하고 black을, 나머지를 자식으로 하고 red로 바꿔줍니다.
Step 6 : 25
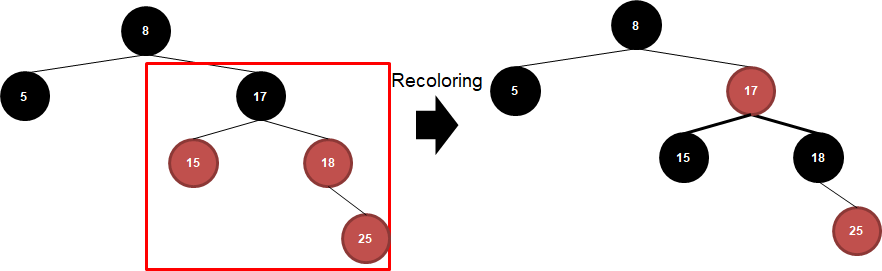
Double Red가 발생했고, 부모와 삼촌 노드 색이 같으므로 Recoloring을 수행합니다.
이번엔 부모의 부모 노드가 루트가 아니니까 Red로 변경해줍니다.
Step 7 : 40
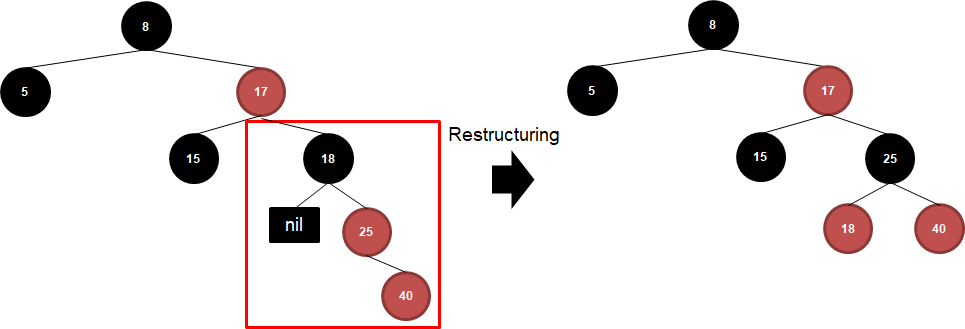
Double Red가 발생했고, 부모와 삼촌 노드 색이 다르므로 Restructuring을 수행합니다.
Step 8 : 80
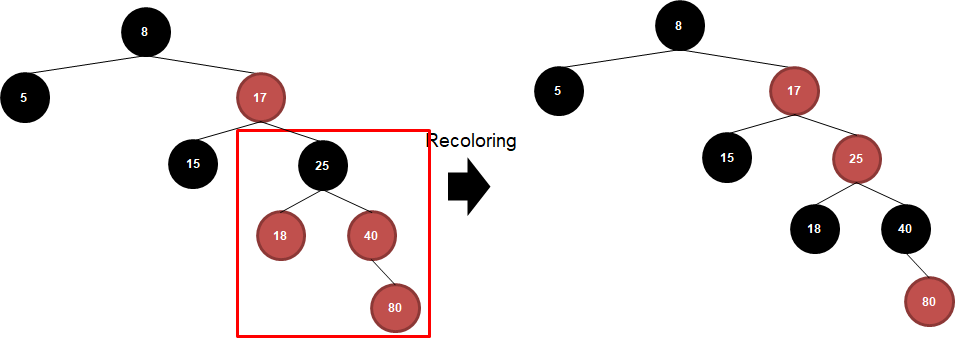
Double Red가 발생했고, 부모와 삼촌 노드 색이 같으므로 Recoloring을 수행합니다.
여기서, 17과 25에 Double Red가 또 발생했습니다. 따라서 이 경우 25 기준 부모와 삼촌 노드가 색이 다르므로 Restructuring을 수행합니다.

복잡도
| Algorithm | Average | Worst Case |
|---|---|---|
| Space | ||
| Search | ||
| Insert | ||
| Delete |
후기
드디어 Red-black Tree를 이해하게 되었네요. 학부생때부터 무슨 소린가 전혀 이해가 안되었는데, 이번 기회에 공부하면서 이해를 하게 되니까 전보다 두뇌회전은 돌아가는 기분이 드네요 ㅎㅎ. 지금의 자신감을 유지하며 계속 공부하는게 중요한 거 같습니다. 계속 분발하겠습니다 (__)
참고
https://nesoy.github.io/articles/2018-08/Algorithm-RedblackTree
http://zeddios.tistory.com/237
