📕 들어가며
오늘은 간단한 프로젝트를 통해
선형회귀의 개념과
관련 라이브러리 사용법에 대하여
정리해보겠습니다.
📕 실습준비
1. 데이터 준비
Salary 데이터 다운로드 받아 주세요 ^^
2. 데이터 분석
# 데이터 읽어오기
import pandas as pd
# "salary_Data.csv" : 읽어오기
df = pd.read_csv("./data/Salary_Data.csv")
df.head()# scatter plot 그리기
import matplotlib.pyplot as plt
x = df["YearsExperience"]
y = df["Salary"]
plt.xlabel("YearsExperience")
plt.ylabel("Salary")
plt.scatter(x, y, color="red", marker="*")
plt.show()<실행결과> :
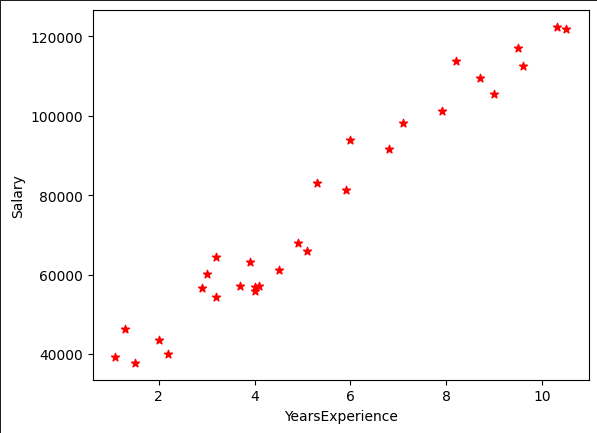
당연한 이야기 이지만
연차가 올라감에 따라 더 많은 연봉을 받는다는
사실을 알 수 있습니다.
그래서 선형 회귀 알고리즘을 사용해
경력을 가지고 연봉을 예측하는
머신러닝 모델을 만들어 보려고 합니다.
3. 선형회귀가 뭔데?!
선형 회귀(線型回歸, 영어: linear regression)란
한 개 이상의독립 변수 X와종속 변수 y와의
선형 상관 관계를 모델링하는 회귀분석 기법이다.
라고 위키백과에 적혀 있군요
간단하게 말하면 선형회귀 알고리즘은
데이터의 특성을 가장 잘 나타낼 수 있는 선을 찾아내는 회귀 알고리즘
으로 이해하시면 됩니다.
예시)
📕 머신러닝 모델 사용해보기
✏️ 1. 학습 데이터 가져오기
# 데이터 읽어오기
import pandas as pd
# "salary_Data.csv" : 읽어오기
df = pd.read_csv("./data/Salary_Data.csv")
df.head()<실행결과> :

✏️ 2. 데이터 분리
# sklearn 을 활용한 선형회귀 모델링을 위해
# 데이터를 train set 과 test set으로 분리한다.
# train set: 머신러닝 모델 학습에 사용되는 데이터
# test set: 머신러닝 모델 평가에 사용되는 데이터
from sklearn.model_selection import train_test_split
x = df.iloc[:,:-1].values # YearsExperience (★★★: 2차원 배열로 가져와야 함)
y = df.iloc[:,1].values # Salary
# 30% 테스트로 사용
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size = 1/3, random_state= 1)
print(len(X_train)) # 20개
print(len(X_test)) # 10개 ✏️ 3. 모델 훈련
# 모델 훈련하기
from sklearn.linear_model import LinearRegression
model = LinearRegression() # y = ax + b
model.fit(X_train, y_train) # train 데이터로 모델 학습# 훈련된 모델로 예측해보기
import numpy as np
# prediction
y_pred = model.predict(X_test)
print(X_test)
print(np.array(y_pred).reshape(10,1))<실행결과> :
근무기간이
5.3년인 sample의 급여를74675.37776747로 예측했다고 해석하시면 됩니다.

# 실제 정답
print(np.array(y_test).reshape(10,1))<실행결과> :

✏️4. 훈련된 모델 평가하기
# 모델 평가하기1
# score : X_test를 모델에 넣어서 나온 결과와 y_test를 비교해서 결정계수 알려주는 함수
# score(결정계수)는 0과 1사이의 값을 가지며
# 이 값이 높을 수록 model의 예측이 정확하다고 판단할 수 있다.
model.score(X_test, y_test)<실행결과> :
결정 계수는 0.92408504...입니다.
모델이 꽤 정확하게 연봉을 예측하고 있습니다.

# 모델 평가하기2
# 평균 절댓값 오차(MAE) : 오차에 절댓값 씌운 값을 평균낸 값
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)<실행결과> :
예측이 정답과 평균적으로 5049달러 정도 차이가 납니다.
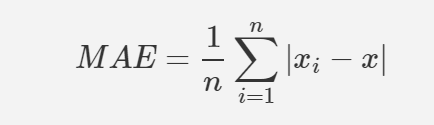
✏️5. 시각화
# model.coef_ : 직선의 기울기
# model.intercept_ : 직선의 y절편
print(model.coef_, model.intercept_)<실행 결과> :

# scatter 시각화
import matplotlib.pyplot as plt
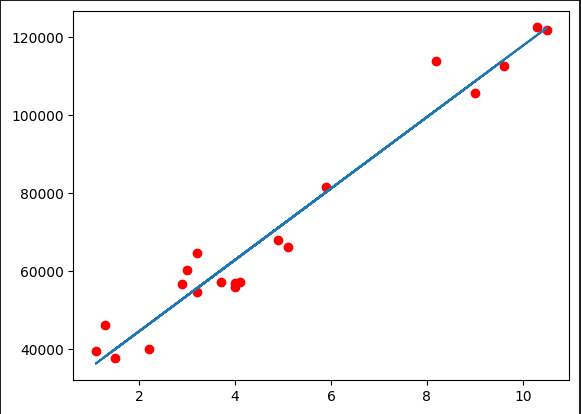
plt.scatter(X_train, y_train, color = "red")
plt.plot(X_train, model.predict(X_train))
plt.show()<실행 결과> :
📕 전체 코드
# scatter 시각화
# linear Regression
import pandas as pd
import matplotlib.pyplot as plt
# "salary_Data.csv" : 읽어오기
df = pd.read_csv("./data/Salary_Data.csv")
df.head()
# scatter plot 그리기
# x : 'YearsExperience'
# y : 'Salary'
x = df["YearsExperience"]
y = df["Salary"]
plt.xlabel("YearsExperience")
plt.ylabel("Salary")
plt.scatter(x, y, color="red", marker="*")
plt.show()
# sklearn 을 활용한 선형회귀 모델링을 위해
# 데이터를 training set 과 test set으로 분리한다 (매우 중요한 개념!)
from sklearn.model_selection import train_test_split
x = df.iloc[:,:-1].values # YearsExperience (★★★2차원 배열로 가져와야 함)
y = df.iloc[:,1].values # Salary
# 30% 테스트로 사용
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size = 1/3, random_state= 1)
# 선형 모델링
from sklearn.linear_model import LinearRegression
model = LinearRegression() # y = ax + b
model.fit(X_train, y_train) # 학습
import numpy as np
# prediction
y_pred = model.predict(X_test)
print("테스트 급여 : ", X_test)
print("\n예측값 : ", np.array(y_pred).reshape(10,1))
print("\n실제정답 : ", np.array(y_test).reshape(10,1))
print("\n모델평가")
print("결정계수 : " ,model.score(X_test, y_test))
from sklearn.metrics import mean_absolute_error
print("평균 절댓값 오차 : ", mean_absolute_error(y_test, y_pred))
print()
# scatter 시각화
plt.scatter(X_train, y_train, color = "red")
plt.plot(X_train, model.predict(X_train))
plt.show()
print()
print("기울기 : " , model.coef_)
print("y 절편 : " , model.intercept_)