📕 들어가며

---

지난 시간에는
cutoff를 한땀한땀 바꿔가며
로지스틱 회귀 알고리즘으로 분류모델의
accuracy를 개선하는 작업을 해보았습니다.

이번 시간에는 Optimize(최적화)에 대해서 배워보고
이를 활용하여 accuracy를 최대로 만들어주는 cutoff를 한 번에 찾아보도록
해보겠습니다.

📕 지난 시간 결과

---

1. 데이터 준비

Social_Network_Ads 데이터 다운로드 받아 주세요 ^^

<컬럼 설명>
1. Age: 나이
2. EstimatedSalary: 추정 연봉
3. Purchased: 상품 구매 여부

2. cutoff 수정해서 accuracy 개선

# <정규화와 cutoff 조정 둘 다 같이 적용>

import pandas as pd

# 데이터 "Social_Network_Ads.csv" 로드
df = pd.read_csv("./data/Social_Network_Ads.csv")

# 데이터 분리하기
from sklearn.model_selection import train_test_split

X = df.iloc[:, [0,1]].values
y = df.iloc[:, 2].values

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

# 데이터 정규화 작업
from sklearn.preprocessing import StandardScaler

sc = StandardScaler()

# 데이터에 정규화 적용
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

# 모델 훈련하기
from sklearn.linear_model import LogisticRegression
classifer = LogisticRegression(random_state=0)
classifer.fit(X_train, y_train)

# predict_proba: X_test의 각 값을 0으로 예측할 확률과 1로 예측할 확률을 보여줌
# 그 중 각 값을 1로 예측할 확률들만 가져옴
prob1 = classifer.predict_proba(X_test)[:,1] # [ 0.45491443, 0.47404153, ... ]

# cutoff 0.48로 수정
cutoff = 0.48 

# Y_pred_new_cutof: 새로운 cutoff를 적용한 예측치
y_pred_new_cutoff = [1 if i > cutoff else 0 for i in prob1]
y_pred_new_cutoff

# 모델 평가하기1
# Confusion matrix.
from sklearn.metrics import confusion_matrix
cmtx = pd.DataFrame(
    confusion_matrix(y_test, y_pred_new_cutoff, labels = [1, 0]),
    index = ['true:purchased(1)', 'true:purchased(0)'],
    columns = ['pred:purchased(1)', 'pred:purchased(0)']
)
print("cmtx : ", cmtx)
print()

# 모델 평가하기2 (다양한 라이브러리 활용하기)
# accuracy 구하기
from sklearn.metrics import accuracy_score
print("accuracy : ", accuracy_score(y_test, y_pred_new_cutoff))

# precision, recall, fscore 구하기
from sklearn.metrics import precision_recall_fscore_support
print("(precision, recall, fscore, support) = ", precision_recall_fscore_support(y_test, y_pred_new_cutoff, average='binary'))

<실행 결과> :

3. 결과 분석

accuracy가 90%나 되기는 하지만
cutoff를 최적화해서 더 높은 accuracy를 얻어보겠습니다.

📕 Optimize(최적화)

---

✏️ optimize가 뭔데?!

optimize(최적화)란 어떤 함수의 최댓값 혹은 최솟값을 찾는 것입니다.
1. 그래프를 그릴 수 있다면 그래프를 그린 후
2. 그 값을 실제로 찾는 과정으로 이루어 집니다.

1. optimize를 연습할 함수를 하나 정의

import numpy as np
from matplotlib import pyplot as plt

# Thanks to https://www.tutorialspoint.com/how-to-plot-a-function-defined-with-def-in-python-matplotlib
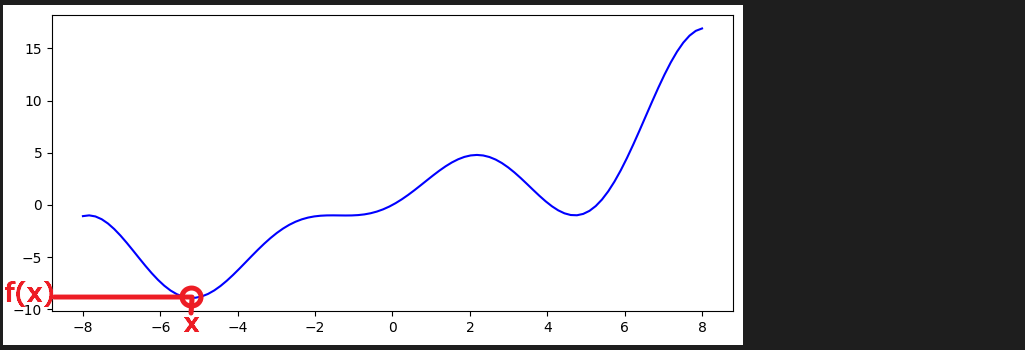
def any_func(x):
   return np.sin(x) + x + x * np.sin(x)

x = np.linspace(-8, 8, 100)

plt.rcParams["figure.figsize"] = [7.50, 3.50]
plt.rcParams["figure.autolayout"] = True
plt.plot(x, any_func(x), color="blue")
plt.show()

<실행 결과> : 아래 그래프에서 x 값과 f(x) 값을 찾아야 합니다.

2-1. optimize 방법1

# optimize 방법1 - minimize 
from scipy.optimize import minimize 

res = minimize(fun=any_func, x0=1, method="nelder-mead", options={'xatol':1e-8,'disp':True})

print("res.x", res.x)
print("res.fun", res.fun)

<실행 결과> : x = -5.18 에서 최솟값 f(x) = -8.91 을 가진다고 찾아줍니다.

2-2. optimize 방법2

# optimize 방법2 - basinhopping
from scipy.optimize import basinhopping # global opt를 찾는 라이브러리

minimizer_kwargs = {"method": "nelder-mead"}
res2 = basinhopping(func = any_func, x0 = 3, minimizer_kwargs=minimizer_kwargs, stepsize=0.5, niter=200)

<실행 결과> : 역시 x = -5.18 에서 최솟값 f(x) = -8.91 을 가진다고 찾아줍니다.

📕 cutoff optimize

✏️ 1. objective_func 정의

# 성능평가 연산 방식을 목적함수(objective function)로 정의한다.
# 주의: minimize 함수에 적용을 위해 1-accuracy, 즉, 오류율 값으로 리턴한다. (Accuracy 기준의 목적함수 구성)

def objective_func(cutoff):
    y_pred_new_cutoff = [1 if i > cutoff else 0 for i in prob1]
    
    return 1- accuracy_score(y_test,y_pred_new_cutoff)

# 예시 실행 : 모델의 default 컷오프 값인 0.5로 테스트해본다.
print("정확도: ", 1 - objective_func(0.5))

<실행 결과> :

✏️ 2. objective_func 개형 파악

# cutoff의 범위는 0 부터 1까지 이지만 개형을 보기위해 x 범위를 조금 더 넓게 잡음
x = np.linspace(-1, 2, 100)
y = [objective_func(j) for j in x]
plt.rcParams["figure.figsize"] = [7.50, 3.50]
plt.rcParams["figure.autolayout"] = True
plt.plot(x, y, color="blue")
plt.show()

<실행 결과> :

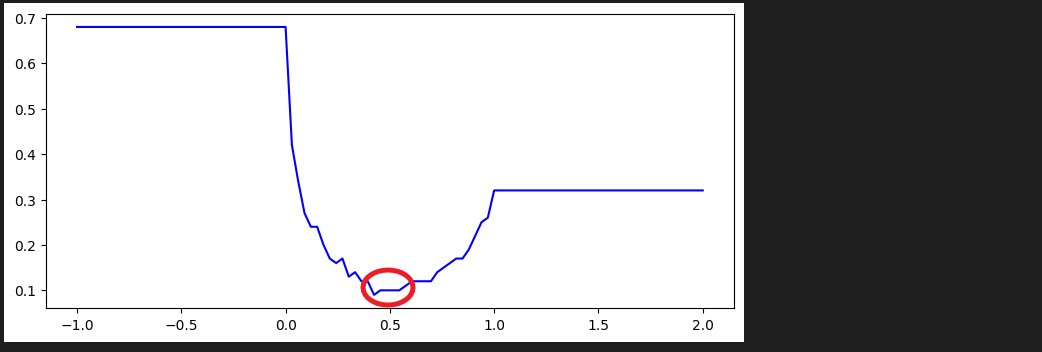
✏️ 3. 최솟값 찾기

# 목적함수를 opt 모델에 적용한다.
from scipy.optimize import minimize 

opt_res = minimize(objective_func, 0.5, method="nelder-mead", options={'xatol':1e-8,'disp':True})

print("cutoff point : ", opt_res.x)
print("정확도 (accuracy) : ", 1-opt_res.fun)

<실행 결과> : cutoff가 0.5375일 때 accuracy가 91로 최대라고 합니다.

✏️ 4. cutoff 최적화 전체 코드

# 분류모델의 정확도 개선 위해
# 정규화와, cutoff 조정, cutoff 최적화 모두 수행
import pandas as pd

# 데이터 "Social_Network_Ads.csv" 로드
df = pd.read_csv("./data/Social_Network_Ads.csv")

# 데이터 분리하기
from sklearn.model_selection import train_test_split

X = df.iloc[:, [0,1]].values
y = df.iloc[:, 2].values

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

# 데이터 정규화 작업
from sklearn.preprocessing import StandardScaler

# X_train, X_test
sc = StandardScaler()

# 데이터에 정규화 적용
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

# 모델 훈련하기
from sklearn.linear_model import LogisticRegression
classifer = LogisticRegression(random_state=0)
classifer.fit(X_train, y_train)

# predict_proba: X_test의 각 값을 0으로 예측할 확률과 1로 예측할 확률을 보여줌
# 그 중 각 값을 1로 예측할 확률들만 가져옴
prob1 = classifer.predict_proba(X_test)[:,1] # [ 0.45491443, 0.47404153, ... ]

# accuracy를 가장 높게 하는 cutoff 찾기
from scipy.optimize import minimize 

def objective_func(cutoff):
    y_pred_new_cutoff = [1 if i > cutoff else 0 for i in prob1]
    
    return 1- accuracy_score(y_test,y_pred_new_cutoff)

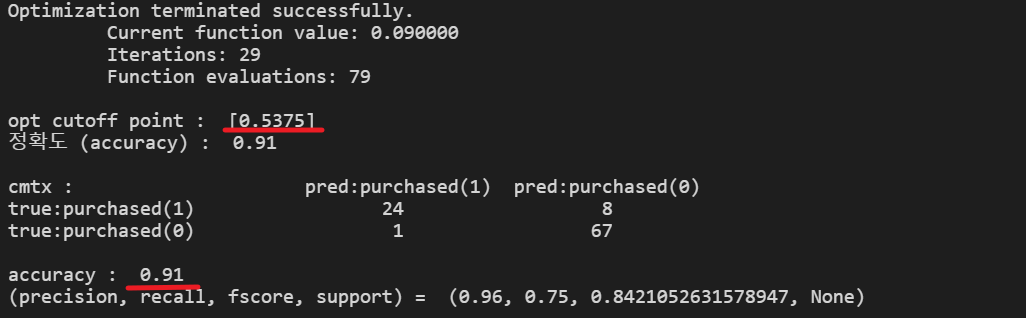
opt_res = minimize(objective_func, 1, method="nelder-mead", options={'xatol':1e-8,'disp':True})

print("opt cutoff point : ", opt_res.x)
print("정확도 (accuracy) : ", 1-opt_res.fun)
print()

# 찾은 cutoff 적용
cutoff = opt_res.x

# Y_pred_new_cutof: 새로운 cutoff를 적용한 예측치
y_pred_new_cutoff = [1 if i > cutoff else 0 for i in prob1]
y_pred_new_cutoff

# 모델 평가하기1
# Confusion matrix.
from sklearn.metrics import confusion_matrix
cmtx = pd.DataFrame(
    confusion_matrix(y_test, y_pred_new_cutoff, labels = [1, 0]),
    index = ['true:purchased(1)', 'true:purchased(0)'],
    columns = ['pred:purchased(1)', 'pred:purchased(0)']
)
print("cmtx : ", cmtx)
print()

# 모델 평가하기2 (다양한 라이브러리 활용하기)
# accuracy 구하기
from sklearn.metrics import accuracy_score
print("accuracy : ", accuracy_score(y_test, y_pred_new_cutoff))

# precision, recall, fscore 구하기
from sklearn.metrics import precision_recall_fscore_support
print("(precision, recall, fscore, support) = ", precision_recall_fscore_support(y_test, y_pred_new_cutoff, average='binary'))

<실행 결과> :