Introduction

RektPunk·2023년 2월 17일

Quantile regression

목록 보기

1/6

Abstract

Regression model은 일반적으로 반응 변수의 Conditional expectation을 파악하기 위해 사용된다. 마찬가지로, Quantile regression은 설명변수와 반응변수 사이의 관계를 파악하기 위해서 사용되며, 이에 더해 반응 변수의 Conditional distribution의 요약 정보를 파악할 수 있어 용이하다.
이 글에서는 Quantile regression의 전반적인 내용들을 소개한다.

Main

Quantile regression의 목적은 Conditional quantile, $\tau \in [0, 1]$ 에 대해서

q_{Y|X}(\tau )=\inf \left\{y:F_{Y|X}(y)\geq \tau \right\}

를 추정하는 것이 목적이다.
Koenker, Ng, and Portnoy (1994) 가 선형 모델 $f_\tau(x) = x^\top \beta$ 와 Check loss (혹은 Tilted absolute loss 라고 불리기도 한다.)를 사용한 목적함수

L(f) = \frac{1}{n} \sum_{i = 1}^n \rho_{\tau}(y_i - f_\tau(x_i)), ~~ \text{where } \rho_{\tau}(u) = u(\tau - \text{I}(u < 0))

를 최소화하는 $f$ 혹은 $f$ 를 구성하는 paramete를 찾음으로써 $\tau$ -quantile 을 추정할 수 있음을 보였다.

여기서 사용된 Check loss 는 indicator function 없이 작성하면

\rho_\tau(u) = \left\{ \begin{array}{cc} u\tau & \text{if } u\geq 0 \\ u(\tau -1) & \text{if } u < 0 \end{array} \right.

처럼 쓸 수 있으며, 이를 시각화하면 아래 그림과 같다.

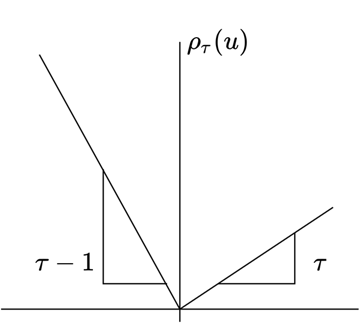
직관적으로 이해하자면 Check loss의 $u$ 부분에 error 인 $y_i - f_\tau (x_i)$ 가 들어간다.
즉, 예를 들어, 0.9-quantile 을 추정할 때 ( $\tau = 0.9$ )는

error > 0 인 경우에 weight 가 0.9,
error < 0 인 경우에 weight 가 0.1,

인 형태로 모수를 추정한다.이에 따라 Optimization에서 양수인 경우의 Loss를 줄이기 위해

$\#(\text{error} < 0): \#(\text{error} > 0) = 9:1$

의 비율로 추정하고자 할 것이고, 이는

$\#(y_i < f_{0.9}(x_i)):\#(y_i > f_{0.9}(x_i))=9:1$

와 일맥상통하여 $f_{0.9}(x_i)$ 는 0.9-quantile 이 된다.

Remarks

최근에도 다양한 모델들이 Quantile regression을 위해서 Check loss를 사용하는 경우가 많다. 차이점은 $f_\tau(x)$ 를 보다 고차원의 함수로 변경한 것이다.

Reference

Koenker, Roger, Pin Ng, and Stephen Portnoy. "Quantile smoothing splines." Biometrika 81.4 (1994): 673-680.

RektPunk

한가한 Data scientist

다음 포스트