[DFS,BitMasking 문제] LEETCODE 78. Subsets

문제

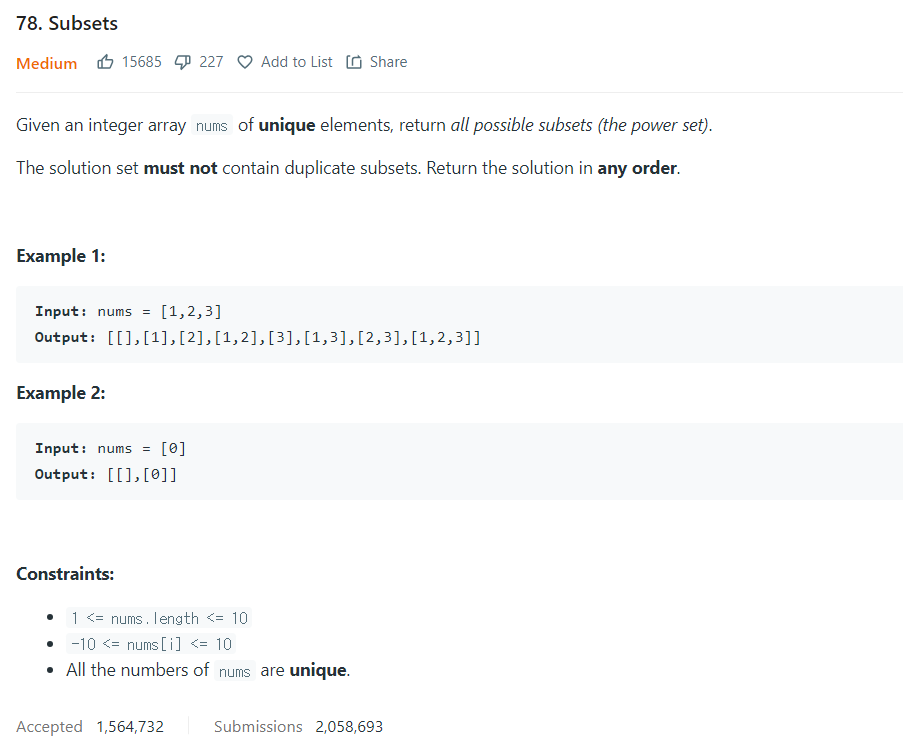
https://leetcode.com/problems/subsets/

문제풀이 1(DFS)

재귀적 방식으로 DFS를 수행하여 인덱스 값을 늘려가면 경우의 수를 계산함.

코드 1(DFS)

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans=[[]]

        n=len(nums)
        def dfs(start,subans):
            ans.append(subans)
            for i in range(1,len(nums)):
                if start+i>=len(nums):
                    break
                dfs(start+i,subans+[nums[start+i]])
            
        for i in range(len(nums)):
            dfs(i,[nums[i]])
        return ans

문제풀이 2(BitMasking)

비트 마스킹 방식으로 주어진 nums에 대해 선택 여부를 관리하는 값을 생성한다.
nums의 자리수를 n이라고 하였을때 0부터 2^n-1 경우는 모든 경우의 수를 포함하게 된다.
ex) nums 배열길이가 2라고 한다면 선택 가능한 조합은 [0,0],[0,1],[1,0],[1,1]이고 이를 2진수라고 생각해보면 0,1,2,3(=2^2 -1)까지의 값이면 모든 조합을 산출 가능함.
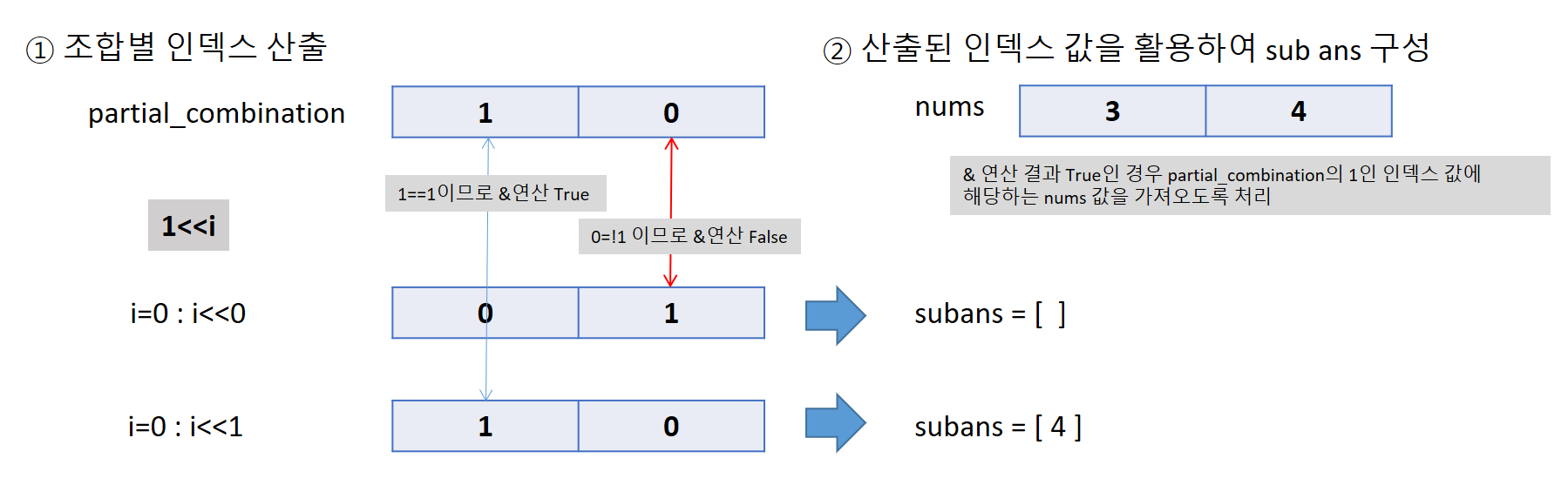
이후에는 이 조합에 대해서 1값의 index를 가지고 부분집합을 구성해야 한다.
이는 partial_combination && 1<<j 의 비트 연산을 통해서 수행한다.
여기서 partial_combination를 편의상 선택 여부의 부분집합으로 보고 해당 부분집합에 대해 1이 존재하는 인덱스를 검침해나간다. 이러한 인덱스 값을 활용하여 subans를 구성하여 누적해나가며 최종 답 ans를 구성한다.

코드 2(BitMasking)

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans,n=[],2**len(nums)
        for partial_combination in range(n):
            subans=[]
            for j in range(len(nums)):
                if j>partial_combination:
                    continue
                if partial_combination&1<<j :
                    subans.append(nums[j])
            ans.append(subans)
        return ans

Lookback

1. 이번 문제에 대해서 DFS 방식과 bitMasking 방식 두가지 해결방안을 통해 접근하였다. 속도 측면에서는 bitMasking이 조금 더 빨랐고 메모리 사용량은 유사했다. 이 문제의 경우 입력크기가 10인데 비트연산 처리시 2^n처리가 필요하므로 입력크기가 커질수록 비트마스킹은 메모리사용량이 급증하게 되어 백트래킹 방식이 더 강정이 있지 않을까 싶다.