[Greedy 문제] LEETCODE 135. Candy

문제

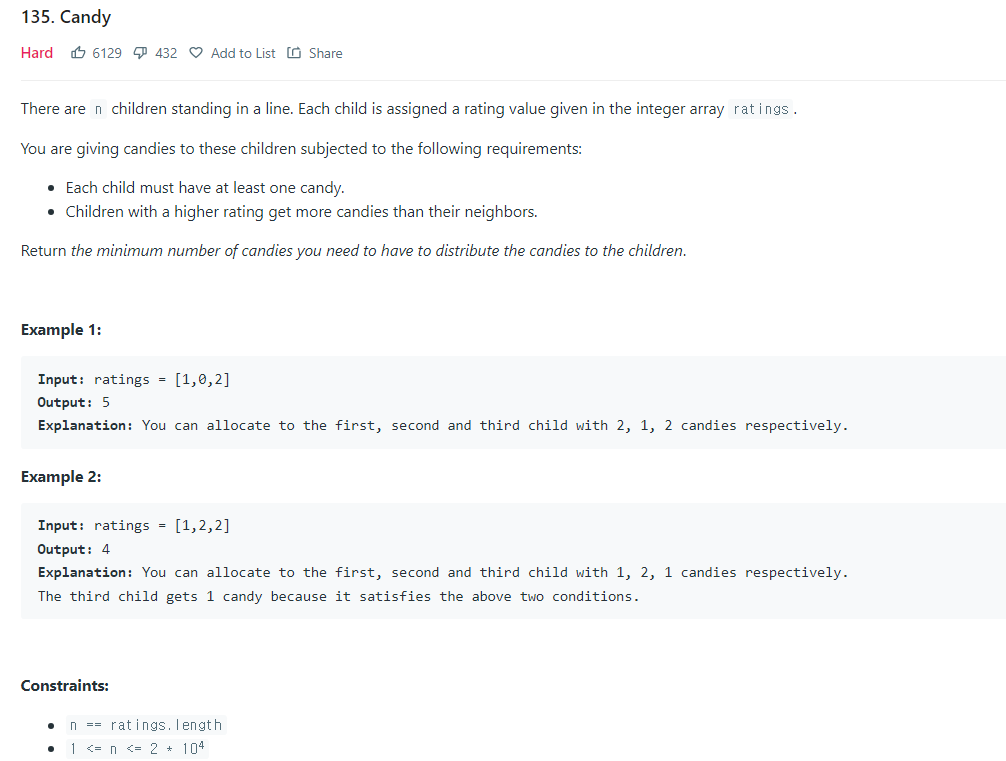
https://leetcode.com/problems/candy/

문제풀이

이번 문제는 학생의 평가 점수에 따라 사탕을 배분하는 문제이다. 이 문제를 접근함에 있어서 우선 케이스를 2가지로 분류하였는데 1.평가가 오름차순으로 증가하거나 같은 구간 2.평가가 내림차순으로 감소하는 구간이다.
오름차순이라면 이전 학생에 비해 점수가 높기 떄문에 이전 학생의 사탕 수에 +1 처리를 하도록 처리하였고 만약 이전 학생의 평가와 동일한 평가라면 사탕을 가장 작게 주기 위해 최소 수량인 1개만 할당하도록 하였다.
내림차순이라면 처리방식이 달라지게 되는데 내림차순 길이가 n인 경우 n->n-1->n-2->..->1 형태로 배분되어야 최소 수량으로 배분이 가능하게 된다. 이를 위해 queue를 선언하여 내림차순 구간을 계산하도록 하였다.
이렇게 계산한 구조에서 핵심적인 처리 방식은 오름차순 or 동일 구간-> 내림차순 구간 등으로 구간 구분이 변경되는 시점이다. 이 시점에 해당하는 학생에게는 각 구간별 값의 max 값을 취하도록 처리해야 한다.
ex) 4->5->6->2 라고 하면 6의 경우 오름차순 구간([4->5->6]) 으로 판단하였을때 3개가 할당 가능하고 내림차순 구간([6->2])로 판단하였을때 2개가 할당 가능하다. 이 떄 2를 할당하게 되면 오름차순 구간의 전제가 거짓이 되므로 3을 할당하도록 처리해야 한다.
소스 코드 상에선 ans 변수에 모든 값을 다 더한 후(2+3) 이후에 최소값을 제거하는 식으로 처리하여 max값을 취하도록 처리하였다.

상세 동작은 아래와 같다.

주요 로직 처리

1. 만약 현재 학생의 평가 점수가 이전 학생보다 크다면 오름차순 구간으로 이전 사탕수에 +1 처리하여 할당한다.
2. 만약 현재 학생의 평가 점수가 이전 학생과 동일하다면 최소수량인 1개만 할당한다.
3. 만약 현재 학생의 평가 점수가 이전 학생보다 작다면 queue에 값을 추가한다.

단 1,2 처리시에 만약 queue에 값이 있다면(=즉 구간 유형이 내림차순에서 오름차순 or 동일 값 구간으로 변경되는 지점) queue를 비우면서 내림차순 구간에서 누적했던 queue 길이에 따른 ans 값을 업데이트한다.이 때의 로직을 살펴보면 큐 길이 n이라고 가정했을때 1+2+..+n 까지의 합으로 처리한다. 이 후 ans 값에 대해 겹치는 구간의 경우 오름차순 or 동일 값 기준으로 계산했을때의 값과 내림차순 기준으로 계산했을 때의 값 n이 중복 계산되어 있으므로 min 값을 제거하여 max 값을 선택하도록 처리한다.

코드

[나의 솔루션]
class Solution:
    def candy(self, ratings: List[int]) -> int:
        def empty_queue(queue, cnt_Candy, ans):
            n = len(queue)
            print(queue,n)
            ans += int((1 + n) * n / 2)
            ans -= min(cnt_Candy, n)
            # while queue:
            #     ans+= j
            #     queue.popleft()
            #     j+=1
            return ans

        
        
        queue,i,n,cnt_Candy,ans=deque(),0,len(ratings),0,0 
        
        
        for i in range(1,n):
            prev_val,cur_val=ratings[i-1],ratings[i]
            if cur_val>=prev_val:
                if i==1:
                    cnt_Candy=1
                    ans+=1
                if queue:
                    queue.append(cur_val)
                    ans=empty_queue(queue,cnt_Candy,ans)
                    queue = deque([])
                    cnt_Candy=1
                    
            if cur_val>=prev_val:
                cnt_Candy= cnt_Candy+1 if cur_val>prev_val else 1
                ans+=cnt_Candy
                continue
                
            if cur_val<prev_val:
                queue.append(prev_val)
                if i==n-1:
                    queue.append(cur_val)
                    ans=empty_queue(queue,cnt_Candy,ans)  
                    queue = deque([])
                    cnt_Candy=1
                continue
                
        return ans if n>1 else 1

[솔루션 소스코드]
class Solution:
    def candy(self, ratings: List[int]) -> int:
        N = len(ratings)
        nums = [1]*N
        
        for n in range(1, N):
            if ratings[n-1] < ratings[n]:
                nums[n] = nums[n-1] + 1
        
        for n in range(N-1, 0, -1):
            if ratings[n-1] > ratings[n]:
                nums[n-1] = max(nums[n-1], nums[n] + 1)
                
        return sum(nums)

Lookback

1. 최초에 queue 내 학생 평가 점수를 계산하여 활용하였으나 생각해보니 내림차순 구간의 경우는 내림차순 구간의 길이만 있으면 계산이 가능하므로 굳이 Queue를 활용하지 않아도 되었을 듯하다.
2. 솔루션 코드를 보니 좌/우 탐색 후 배열의 합 처리를 통해 계산하는 구조였다. 좌/우 탐색을 한번씩 하여 계산하는 문제는 어려번 접했었는데 이번 문제에 활용하지 못한 부분은 좀 아쉬웠다. 활용했다면 소스가 조금 더 깔끔하지 않았을까 싶다.
3. 이번 문제를 풀면서 가급적 속도가 빠른 솔루션을 만들도록 하였다. 솔루션 소스코드의 경우는 정탐색,역탐색,sum(nums)처리로 O(N)을 세번 처리하는데 나의 코드는 최선의 경우 1번,최악의 경우 2번 탐색하도록 개선한 소스로 개발하였다.