🤖 재귀(recursion)
어떤 문제를 해결할 때, 구조는 동일하지만 더 작은 경우를 해결함으로써 그 문제를 해결하는 방법을 재귀(recursion)라고 한다. 함수를 자바스크립트 코드로 구현하다가, 실행과정 중에 자기 자신을 호출하기도 하는데 이러한 호출 방식을 재귀 호출이라고 한다.
(어떤 함수가 스스로를 호출 하는 것, programming concept)
function foo(){
foo();
}재귀는 반복할 구문을 함수 단위로 분리해, 특정 조건이 만족할 때까지 실행하는 패턴으로 볼 수 있다.

재귀는 무한 반복을 방지하기 위해 반드시 탈출 조건이 있어야 한다.

🦾 재귀의 장점과 단점
장점: 알고리즘이 재귀로 표현하기에 자연스러울 경우, 프로그램의 가독성이 좋다.
단점: 값이 리턴되기 전까지 호출마다 call stack을 새로 생성하므로, 메모리를 많이 사용한다.
🦾 재귀는 언제 사용하는게 좋을까?
- 주어진 문제가(구조는 비슷하고) 더 작은 문제로 나뉘어 질 수 있는 경우
- 중첩된 루프가 많거나 중첩의 정도(number of loops)를 미리 알 수 없는 경우
사실 모든 재귀 함수는 재귀 호출 없이 while, for loop으로 표현이 가능하다. 하지만 재귀를 사용가능한 경우, 재귀를 사용한 코드가 대부분 더 간결하고 일부의 경우 이해하기가 쉽다.

하노이의 탑과 조합(combination) 문제를 재귀와 그렇지 않은 경우로 비교해보자! 이 밖에도 재귀는 알고리즘 문제의 많은 부분을 차지한다.
재귀적 사고 연습하기
🦿 1. 재귀 함수의 입력값과 출력값 정의하기
재귀 함수를 통해 어떤 문제를 풀고자 하는 지, 즉 우리의 목표를 정리하는 데 도움이 된다. 문제를 가장 추상적으로 또는 가장 단순하게 정리하는 것이다.
🦿 2. 문제를 쪼개고 경우의 수를 나누기
주어진 문제를 어떻게 쪼갤 것인지 고민한다. 어떤 기준을 정하고 그 기준에 따라 문제를 더 큰 경우와 작은 경우로 구분할 수 있는지 검토해보자. 일반적으로 입력값이 이 기준을 정하는 대상이 된다. 이 때 중요한 관점은 순서와 크기이다. 주어진 입력값 또는 문제 상황을 크기를 기준으로 구분할 수 있거나, 순서를 명확하게 정할 수 있는지를 살펴보는 것이 도움이 된다. 그리고 구분된 문제들을 푸는 방식이 같다면, 문제를 제대로 구분한 것이다. (문제의 입력값에 따라 경우의 수를 나누는데 일반적으로 문제를 더 이상 쪼갤 수 없는 경우와 그렇지 않은 경우로 나눈다)
🦿 3. 단순한 문제 해결하기
문제를 여러 경우로 구분한 다음에는 쉬운 문제부터 해결한다. 이를 재귀의 기초(base case)라고 부른다. 재귀의 기초는 나중에 재귀 함수 구현 시 재귀의 탈출 조건(재귀 호출이 멈추는 조건)을 구성하게 된다.
🦿 4. 복잡한 문제 해결하기
남아있는 복잡한 경우를 해결한다.
🦿 5. 코드 구현하기
일반적인 재귀 함수의 템플릿, 재귀 함수 연습에 활용해보자!
function recursive(input1, input2, ...) {
// 재귀의 기초 (base case)
if (문제를 더 이상 쪼갤 수 없을 경우){
return 단순한 문제의 해답;
}
// recursive case
// 그렇지 않은 경우
return 더 작은 문제로 새롭게 정의된 문제
// 예1. someValue + recursive(input1Changed, input2Changed, ...)
// 예2. someValue + recursive(input1Changed, input2Changed, ...)
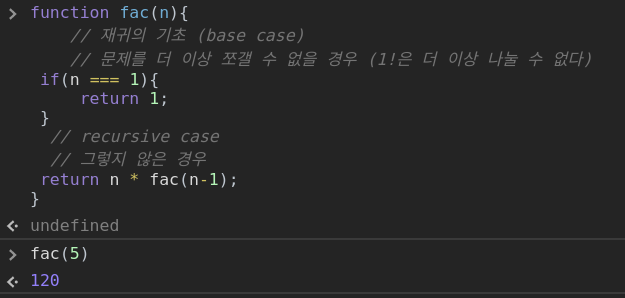
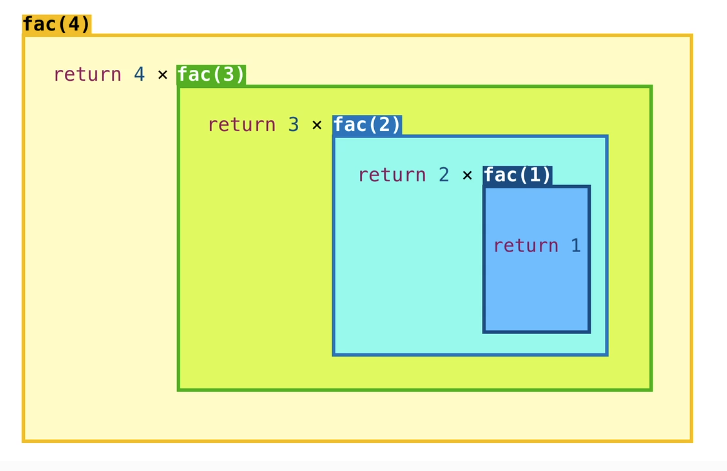
}🦾 factorial로 알아보는 재귀
5!
= 5 x 4 x 3 x 2 x 1
= 5 x (4 x 3 x 2 x 1) = 5 x 4!
= 5 x 4 x 3!