백준 15686번 : 치킨 배달

[문제 분석]

위 문제에서 핵심적인 부분은 다음과 같았다.

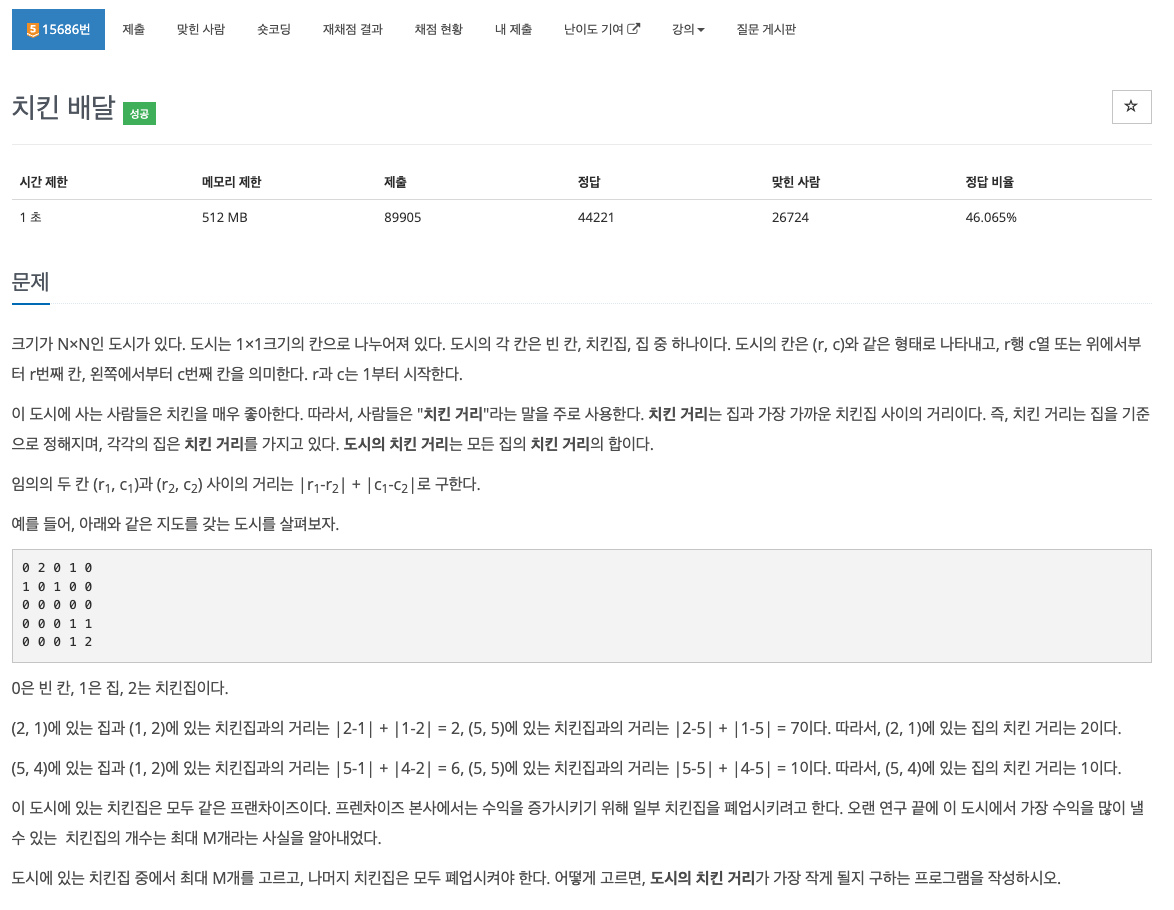
1. 위 문제는 빈칸, 치킨집, 집으로 구성된 도시에서 집과 치킨 집 사리의 거리, "치킨 거리"를 구하기

2. 최대 M개의 치킨집만을 선택하여 최소가 되는 도시의 치킨 거리 구하기

[접근 방식]

• 우선, 입력의 크기가 N(2 ≤ N ≤ 50)과 M(1 ≤ M ≤ 13)으로 굉장히 작기 때문에 완전탐색과 같은 O(N)의 기법으로 문제를 접근하게 되었다.

• 가장 처음에 떠올렸던 방식은 치킨집 하나당 모든 집과의 치킨 거리를 구해 합이 최소가 되는 치킨집만을 남기는 방식이었다.

• 하지만 이러한 방식은 치킨집 하나에 치킨 거리가 최소인 집들이 여러 개가 될 수 있다는 점과 M개의 치킨집을 선택하는 과정이 제대로 반영되지 않는다는 문제가 있었다.

• 따라서 떠올렸던 알고리즘은 다음과 같다!

	1. M개의 치킨집을 선택하기
    2. 모든 집들에 대해서 선택된 치킨집들과의 치킨 거리를 모두 구하기
    3. 각각의 집에 대해서 최소가 되는 치킨 거리만 합산하기
    4. M개의 치킨집을 선택하는 모든 경우의 수에 대해서 이 과정을 반복하기
    
    즉, M개의 치킨집을 선택하는 과정은 BackTracking 방식을 통해 구현, 
    모든 집에 대해 치킨 거리를 구하기 위한 이중 for문으로 이를 구현하면 될 것이라고 판단하였다.

[소스 코드]

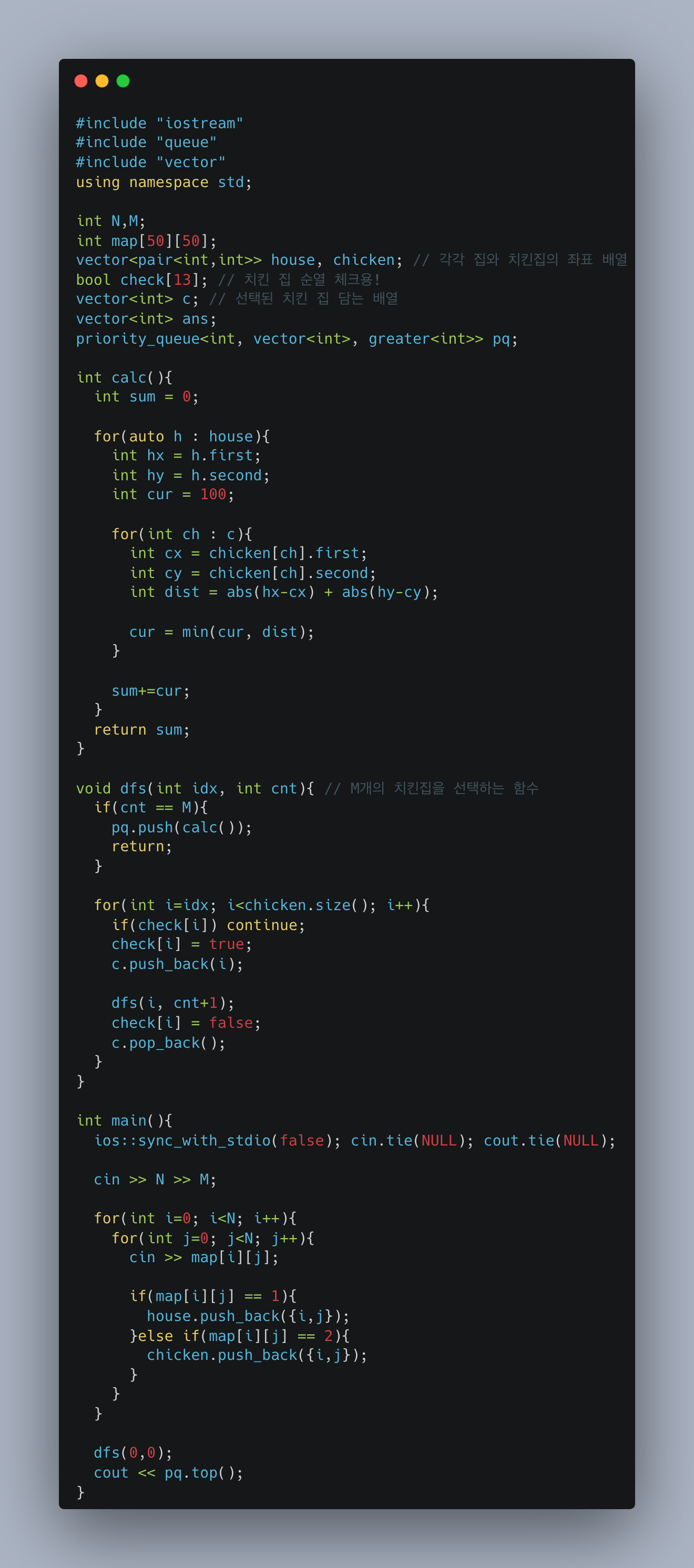
[코드 분석]

    BackTracking 기법을 사용한 dfs 함수를 통해 M개의 치킨집을 선택하고, 
    선택 이후에 치킨 거리를 계산하는 calc 함수가 실행되게 된다.
    
    이중 for문을 통해 모든 집에 대해서 선택된 M개의 치킨집과의 치킨 거리를 계산하게 되며 
    가장 작은 치킨 거리만이 도시의 치킨 거리에 더해지게 된다. 
    
    해당 과정을 M개의 치킨집을 선택하는 모든 경우의 수에 대해 수행하게 되며
    각 과정에서의 값들을 priority queue에 넣어 최소 값을 찾아내는 방식으로 구현하였다!
    
	마지막 최소 값을 구하는 과정에서 굳이 pq를 사용하지 않고 구현하더라도 무방하다.