백준 2589번 : 보물섬

[문제 분석]

위 문제에서 핵심적인 부분은 다음과 같았다.

1. 위 문제는 육지(L)와 바다(W)로 구성된 지도에서 보물이 위치한 두 곳을 찾기

2. 보물이 묻혀 있는 두 곳 사이를 최단 거리로 이동하는 시간 출력하기

[접근 방식]

• 우선, 입력으로 세로의 크기, 가로의 크기가 주어지게 되는데 모두 50이하의 정수 값으로 굉장히 작기 때문에 완전탐색과 같은 O(N)의 기법으로 문제를 접근하게 되었다.

• 가장 먼저 떠올렸던 방식은 육지의 모든 지점에 대해 그래프 탐색을 하며 각 지점에서 갈 수 있는 최장 거리를 체크하는 방식이었다.

• 모든 지점에 대해 bfs를 진행해주어야 하지만 입력의 크기가 매우 작기 때문에 충분히 가능할 것이라고 생각했다.

• 따라서 떠올렸던 알고리즘은 다음과 같다!

	1. 특정 육지를 시작점으로 bfs를 실행하기
    2. 각각의 탐색에서 도달 가능한 최장 거리를 기록하기
    3. 위 과정을 모든 육지에 대해서 진행하고 최장 거리를 갱신하기
    
    즉, 특정 지점에서 갈 수 있는 최장 거리를 구하는 과정은 BFS 방식으로 구현, 
    이중 for문으로 모든 육지를 탐색하는 방식으로 구현하면 될 것이라고 판단하였다.

[소스 코드]

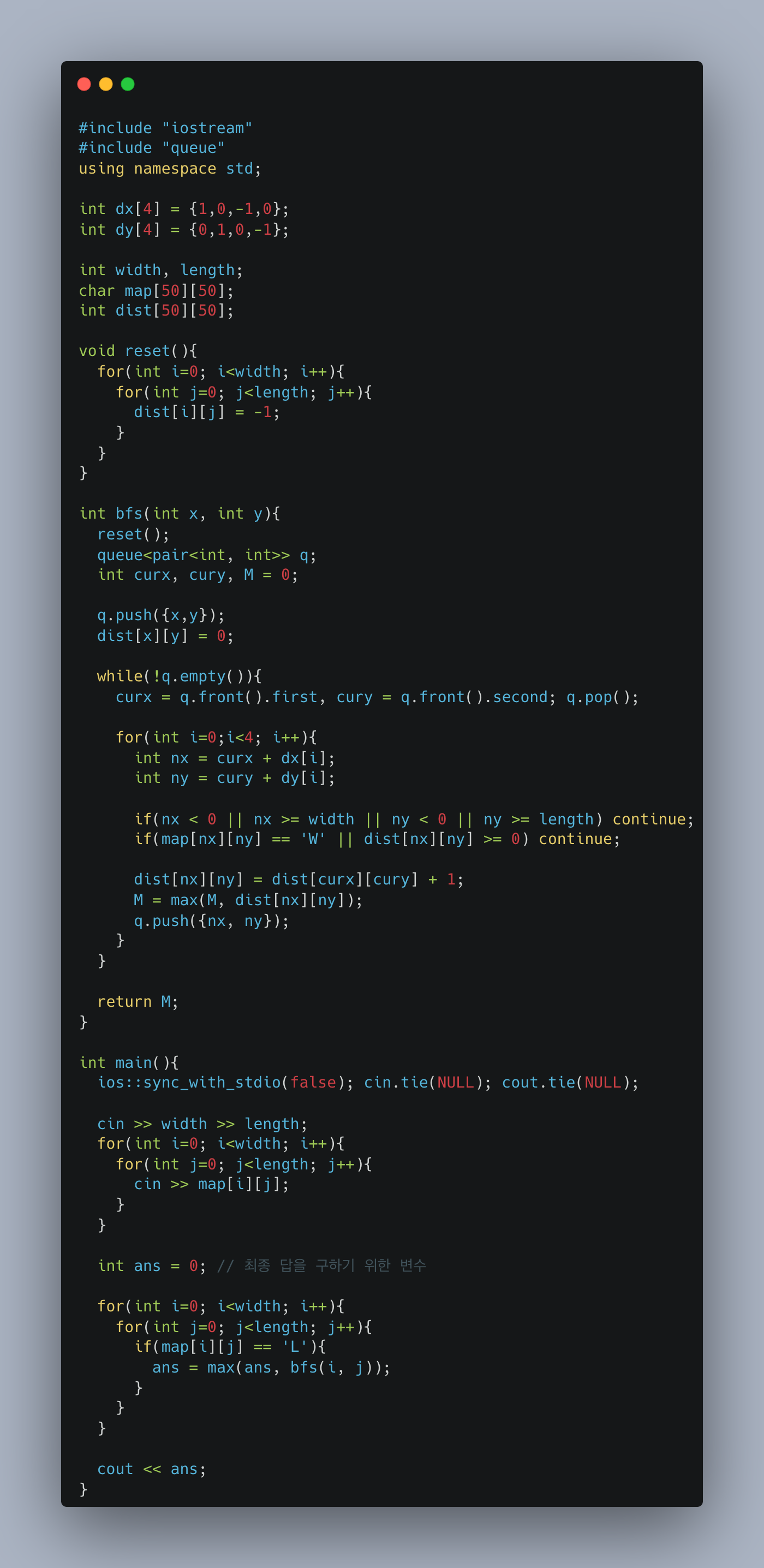
[코드 분석]

    최장 거리를 기록하기 위한 dist 배열과 이를 초기화하는 reset 함수
    
    dy,dx 테크닉을 활용한 queue 기반의 bfs 함수 
    
    한 지점을 방문할 때마다 거리를 갱신해주고 해당 거리가 최장 거리라면 이 또한 갱신!
    
    위 과정들을 모든 육지에 대해서 실행하여 최종 답안 도출!

[고찰]

    사실 이번 문제를 풀면서 꽤 오랜 시간이 걸렸었다.
    그 이유는, 기존의 완전 탐색 방식이 아니라 탐색의 가짓수를 줄이려는 시도를 했었기 때문이다.
    
    떠올렸던 방식은 다음과 같다.
    
    1. 무작위로 선택된 육지에서 bfs를 실행한다.
    2. 첫 번째 bfs가 끝나는 지점에서 두 번째 bfs 실행
    3. 두 번째 bfs를 실행하며, 가장 멀리 떨어진 거리 파악
    4. 해당 과정을 모든 육지 그룹에 대해서 실행
    
    기존 방식대로라면 육지의 모든 지점에 대해서 bfs를 실행해야 했었기 때문에 
    가로 * 세로 크기를 N이라 할 때, 최악의 경우 O(N^2)의 시간 복잡도를 지녔을 것이다.
    
    하지만 위 방식대로라면 육지의 그룹이 가장 많아지는 순간(N/2개, 체스판과 같은 형태)이 최악의 경우가 되며,
    이 경우의 시간 복잡도는 O(N^2/4)이기 때문에 훨씬 빠를 것이라고 생각했다.
    
    단순히 생각해보아도 문제의 예제와 같은 상황이 있더라도 기존 방식은 'L'의 개수만큼의 bfs를 실행하는 반면,
    위 방식은 각 육지 그룹당 bfs 2번씩 진행하면 되기 때문에 총 4번만 실행하면 된다!
    
    하지만 위 같은 방식으로 코드를 구현했으나 정답을 얻어내지는 못했다,,,
    
    내가 생각한 실패의 원인은 크게 2가지이다.
    
    1. 정말 단순 코드 실수 
      :수 많은 디버깅을 하며 대부분의 예제들을 다 통과하였지만 그래도...
    
    2. 기하학적 판단 오류 
      : 그래프에서 특정 지점에서 도달 할 수 있는 지점을 Dead-end, 막다른 길이라고 생각하였고 
      이 Dead-end에서 탐색을 한 번 더하게 되면 반드시 해당 그래프에서 
      도달할 수 있는 최장 거리를 구할 수 있을 것이라고 판단하였다.
      하지만 이는 증명이 되지 않은 본인의 머릿속에서 나온 판단이었기에 틀릴 가능성이 있다고 생각한다.

    충분한 고민의 시간을 가졌고 여러 자료들을 찾아보았지만 아직 어떤 이유로 틀린 지 잘 모르겠다...
    
    그래도 뒤돌아보기 위한 고찰을 남기며 글을 마무리하도록 하겠다!