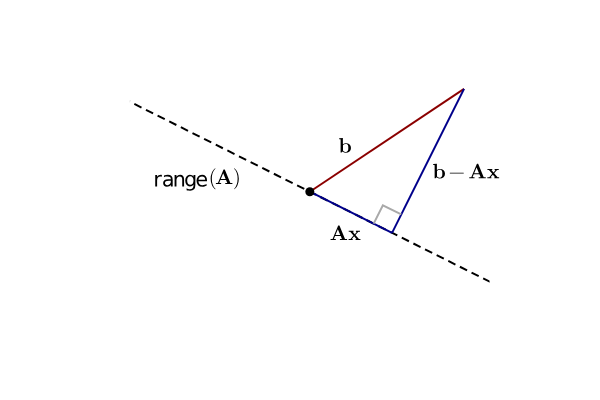
정사영의 기하학적 의미

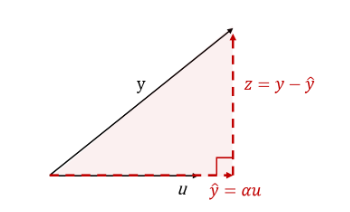
그림으로 부터 설명을 해보자. 우선 unit vector $y$와 $u$ 벡터가 있다고 할 때 ($||y||=1, ||u|| =1$), 벡터의 정의에 의하면, $y$는 $u+z$로 표현할 수 있다.
(주의해야할 점은 u가 unit vector이기에 $\hat y = \alpha u$로 표현한 것이지, unit vector가 아니라면 $\hat y = \alpha \frac{u}{||u||}$로 정의해야한다. )
이때의 두 벡터의 residual(잔차) $z = y-\hat y$로 표현할 수 있을 것이고,
$y$를 u에 정사영 내렸을 때의 $\hat y$는 u의 scalar배 한 어떤 벡터라고 가정해보자.

이제 $y$와 $u$의 관계를 구하기 위해서 두 벡터를 내적해보자.

$y\cdot u =(\hat{y}+z)u$ , where $z = y-\hat y$
$\quad\quad=(\alpha u + z)u$ , where $\hat y = \alpha u$
$\quad\quad=\alpha ||u||^2 +zu$ , where $\quad z \perp u=z\cdot u= 0$
$\quad\quad=\alpha ||u||^2$
이를 $\alpha$에 대해서 다시 정리하면,
$\alpha = \frac{y\cdot u}{||u||^2} = \frac{y\cdot u}{u\cdot u}$

여기서 $y$를 $u$에 정사영 한 벡터 $\hat y =proj_u(y)$로 표현하면 다음과 같다.

$proj_u(y) =\alpha u$
$\quad\quad\quad\quad=\frac{y\cdot u}{||u||^2} u$

즉, $\hat y$는 $y$와 $u$의 내적에 $u$의 크기를 나눠준 다음, $u$ vector의 방향을 곱해준 것이다.

---

이때 $\hat{y}$를 벡터 $y$의 $u$에 대한 정사영 (orthgonal projection of $y$ onto $u$)라고 하고, $z$는 $u$에 수직인 $y$의 벡터 성분이다.
이제, 벡터 $u$가 어떠한 span $W$ 위의서의 한 벡터라고 가정해보자.
결국 $\hat y$는 subspace $W$에 대한 벡터 $y$의 정사영이라고 정의할 수 있다.
즉, $\hat{y} = proj_w(y) , \quad W=span(u)$

---

cosine과 정사영의 관계

정사영의 정의를 사용하여

$\hat y = proj_u(y) = \frac{y\cdot u}{u\cdot u}\cdot u$

위에서의 그림을 cosine$\theta$를 사용하여 표현해보자.
기하학에서 두 벡터의 내적은 $a\cdot b = ||a|| \times ||b|| \times cos \theta$로 정의된다. 이를 바탕으로 다시 적어보면,

$Cosθ = \frac{y\cdot u}{||y||||u||}$
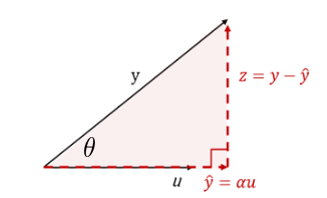
여기서 $\alpha$에 대해서 생각을 해보자. 두 벡터 $y$와 $u$의 길이가 1 이므로, $y,u$는 방향만을 가진다. 즉, $\hat y = \alpha u$라는 것은, $\alpha$는 정사영한 벡터 $\hat y$의 길이라고 해석할 수 있다.

이는 곧, $y$에서 $u$로의 Length of projection이라는 것이다.
즉, $\alpha = \frac{y\cdot u}{||u||^2}$
$\;\quad\quad=\frac{y\cdot u}{||y||||u||}\times||y||$
$\;\quad\quad=cos\theta \times||y||$

$\hat y = proj_u(y) = \alpha \times \frac{u}{||u||}$
$\quad\quad\quad\quad\quad\quad= Cos \theta \times ||y|| \times \frac{u}{||u||}$

기하학 적인 해석

Cosine similarity $Cos\theta = \frac{A\cdot B}{|B||A|}$로 정의 되는데, 이는 무슨 의미를 가질까?
극단적인 경우를 생각해보자.

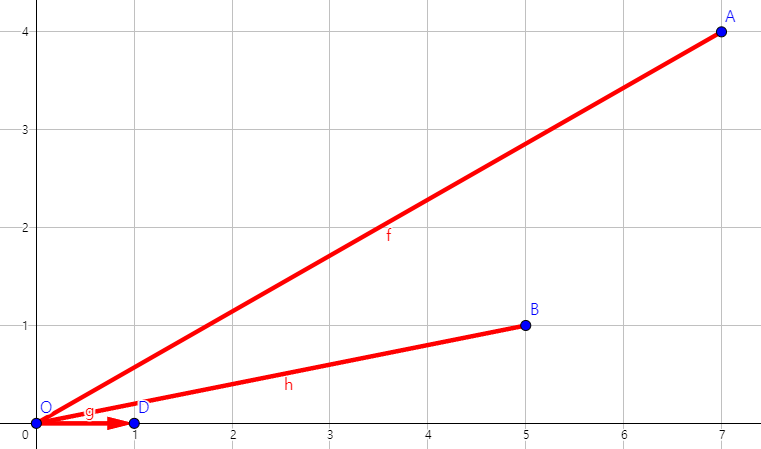
A = [7,4]
B = [5,1]
C = [1,0]

A와 B를 C에 대해서 내적을 하면,
$A \cdot C^T = 7, B \cdot C^T =5$
우리가 보기엔 $B$가 $A$보다 $C$와 더 유사해 보이지만, 내적을 할 경우는 그렇지 않다. 그렇기에 cos similarity는 각 norm을 나눠주는 것인데, 각각에 대해서 norm을 나눈뒤 다시 해보면,

import numpy as np

# Given vectors
A = np.array([7, 4])
B = np.array([5, 1])
C = np.array([1, 0])

# Calculating norms
norm_A = np.linalg.norm(A)
norm_B = np.linalg.norm(B)
norm_C = np.linalg.norm(C)

norm = [norm_A, norm_B, norm_C]
print("norm_A",norm_A)
print("norm_B",norm_B)
print("norm_C",norm_C)
>>>
norm_A 8.06225774829855
norm_B 5.0990195135927845
norm_C 1.0

||A|| ≈ 8.06
||B|| ≈ 5.10
||C|| = 1

# Calculating cosine similarity between A and C
cos_sim_A_C = np.dot(A, C) / (norm_A * norm_C)

# Calculating cosine similarity between B and C
cos_sim_B_C = np.dot(B, C) / (norm_B * norm_C)

cos_sim_A_C, cos_sim_B_C
print("cos_sim_A_C",cos_sim_A_C)
print("cos_sim_B_C",cos_sim_B_C)

>>>
cos_sim_A_C 0.8682431421244593
cos_sim_B_C 0.9805806756909202

Cos(A,C) = 0.86
Cos(B,C) = 0.9

B가 A보다 C에 유사하다는 것을 확실하게 볼 수 있다.

• 결론적으로 cosine similarity $Cos\theta = \frac{A\cdot B}{|B||A|}$
  에서 Norm을 나눠 주는 것은 정사영의 vector를 두 벡터 A,B의 방향만을 반영한다는 의미이고,
  scale만큼을 나눠줌으로서, 계산할 때의 편의성 관점도 있다.

• 다른 의미로, 내적을 한다는 것은 $A\cdot B = Cos\theta \times |B||A|$ 로 생각할 수 있는데, 이는 벡터의 방향 뿐($cos \theta)$뿐만 아니라 벡터의 크기까지 고려하여 유사도를 측정하겠다는 의미이다. 이 관계성을 사용한 것이 $Attention\; Score$이다.

Normal Equation

Cos $\theta$와 projection을 이해하였으니, Normal Equation에 대해서도 생각해보자.
선형 방정식을 $Ax = b$를 푼다는 것은, b라는 vector가 Linear operator$A$를 사용하여 x를 변형시켜 표현할 수 있다는 것으로 해석할 수 있다. 그러나, 만약 b의 rank가 $A$ matrix의 rank보다 크다면? 즉, rank deficiency하다면? b는 $Ax$로 표현할 수 없다. 즉, $rank(b) > rank(A)$의 경우는 문제를 어떻게 풀 수있을까?
이는 residual의 문제로 생각해볼 수 있다. 아래의 그림은, b라는 vector가 $Ax$로 표현할 수 없을 때를 간단하게 그림으로 그린 것인데, $b$ vector를 $Ax$로는 표현할 수 없기에, 가장 가까운 값으로 approximateion하는 방법은 바로 projection을 하는 방법이다.

즉, 우리의 목표는 $b-Ax=r$이라고 가정하면, $||r||_2^2\approx 0$으로 하는 것이 목적이다.(거리가 최소화 되게끔 하고 싶다.)
즉, $||r||_2^2 = 2A^TAx-2A^Tb$ 여기서 $||r||_2^2=0$이 되게 하고 싶으므로,
$2A^TAx-2A^Tb = 0$
$A^TAx = A^Tb$가 성립한다.
이러한 형태를 Normal equation이라고 정의한다.