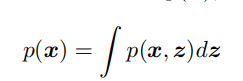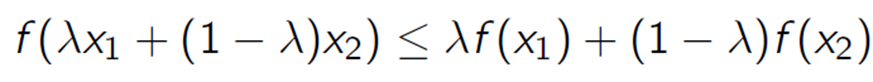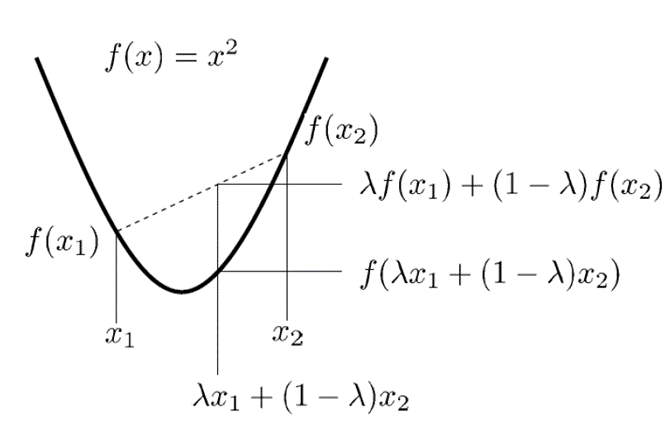Background

Denoising Diffusion Probabilistic Models(DDPM)에서 나오는 수식은 많은 trick 및 유도 과정을 통해서 나온 수식이기 때문에, 논문을 보고서 유도하는 것은 사실 매우 어렵다. 이에 Understanding Diffusion models: A Unified Perspective라는 논문(Survey paper?)에서 그 수식을 자세하게 유도하는데, 그 과정을 정리하고자 한다. 하나의 Page에 담기에는 양이 많아서, 크게 3 Part로 나누어서 설명하려고 한다.

Summary

• ELBO는 확률의 2가지 성질(Marginalize, chain rule)을 사용해서 각각 증명할 수 있다.
• VAE는 ELBO를 사용하여 유도할 수 있는데, 이때 $q_\phi(z|x)$의 output이 Gaussian이 되도록 한것.
• VDM이란 VAE에서 consistency term이 붙은 것을 의미하는데, 이 유도과정은 3가지 제약 조건을 통해서 유도할 수 있다.

Introduction : Generative model

우선 ELBO를 살펴 보기전, 생성 모델의 목적에 대해서 생각을 해보자. 생성 모델이라는 것은 우리의 모델이 true distribution $p(x)$를 찾아내는 것이라고 할 수 있다. Manifold의 관점에서 생각해보면, 전체적인 확률 공간이 존재한다고 할 때, 생성 모델이라는 것은 Target으로 하는 Manifold를 찾은 다음, Manifold에서 Sampling을 진행하는 것이다.

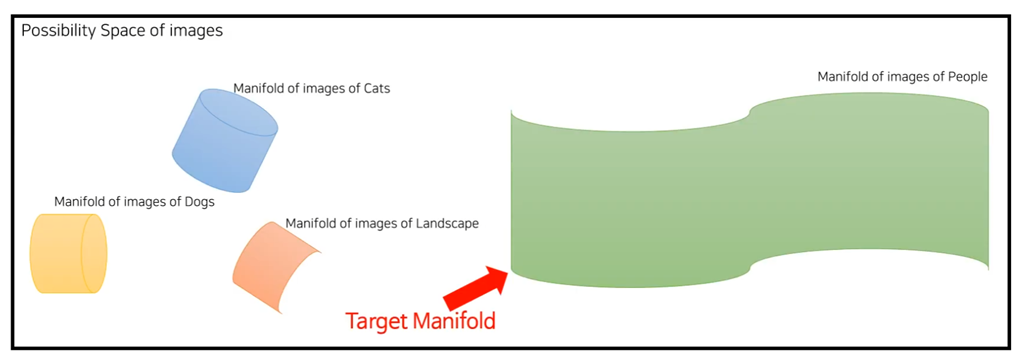
참고

이를 다시 정리하면, $p(x;\theta)$를 모델링하고, 모델에서 값을 넣어 sampling을 하는 것이 생성 모델의 목적이다.

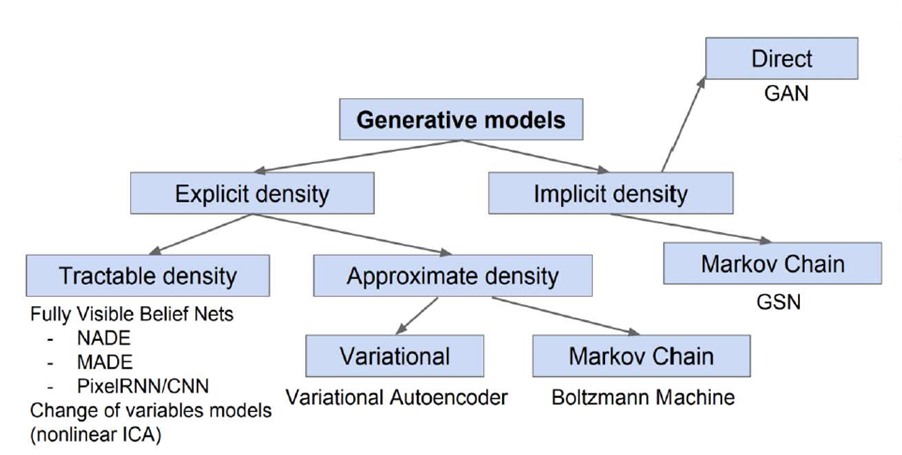
Ian J. Goodfellow, Tutorial on Generative Adversarial Networks, 2017에서는 여러가지의 타입으로 생성 모델을 분류하였다.(2017년 자료 인것을 감안)

---

최근 자주 사용되는 생성 모델은 크게 4가지의 모델이 눈에 띄는 것을 알 수 있다.

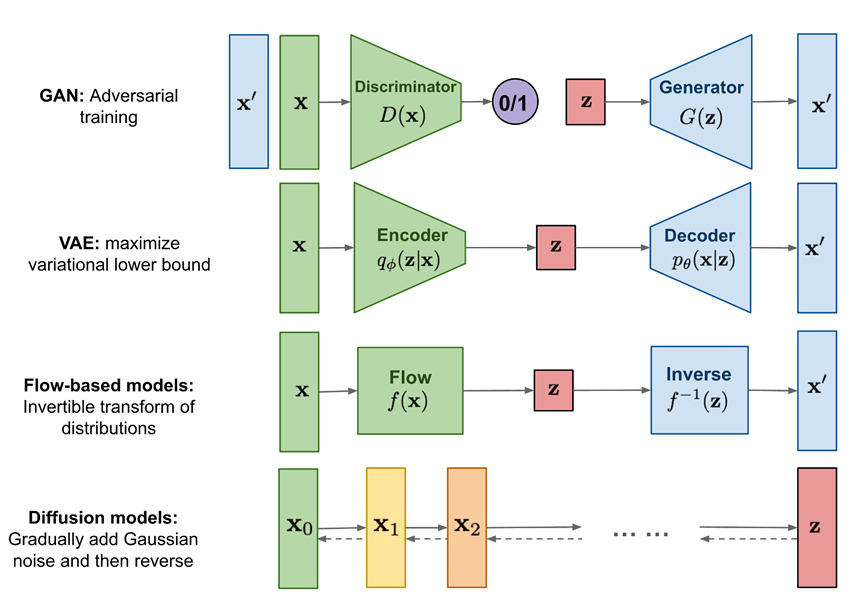
그림

간략하게 설명을 하면,

• GAN : Adversarial manner(Discriminator & Generater)로 학습을 진행한다.
• VAE : AutoEncoder의 구조에서 ELBO와 latent vector의 output이 Gaussian임을 가정하여 진행한다.
• Flow based models : 복잡한 확률 분포를 변환을 통해 간단한 기본 분포(예: 정규 분포)로 학습하려고 한다.
• Diffusion : Noise를 확산 시킨 다음 Noise를 제거하는 방식으로 샘플링을 진행한다.

본 내용은 VAE와 Diffusion에 대해서 자세한 설명을 진행하려고 한다.

Sampling

ELBO를 살펴 보기전 sampling의 정의를 수학적으로 정의해보면, 샘플링이란 target distribution의 Inverse CDF(ICDF)를 구하고, ICDF에 확률 값을 넣었을 때의 얻어진 값을 의미한다. 즉, 그림으로 보면 다음과 같다.

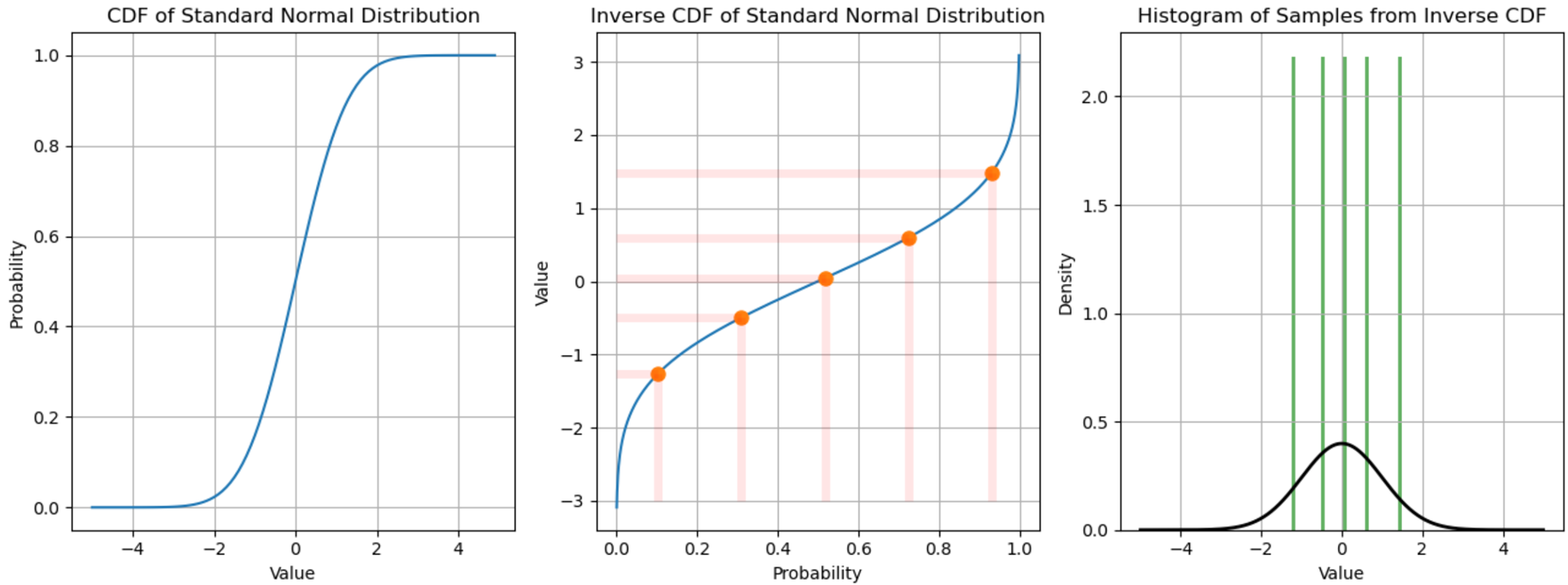
가우시안 분포의 CDF(왼쪽)을 구하고, ICDF(가운데)를 계산한 다음 확률 값을 넣었을 때의 해당하는 점을 그려보았다. 각 해당하는 점을 원래의 가우시안과 비교하여 histogram을 그려보면 원래 분포를 따르는 것을 볼 수 있는데(오른쪽), sampling을 좀 더 세밀하게 진행해보면,

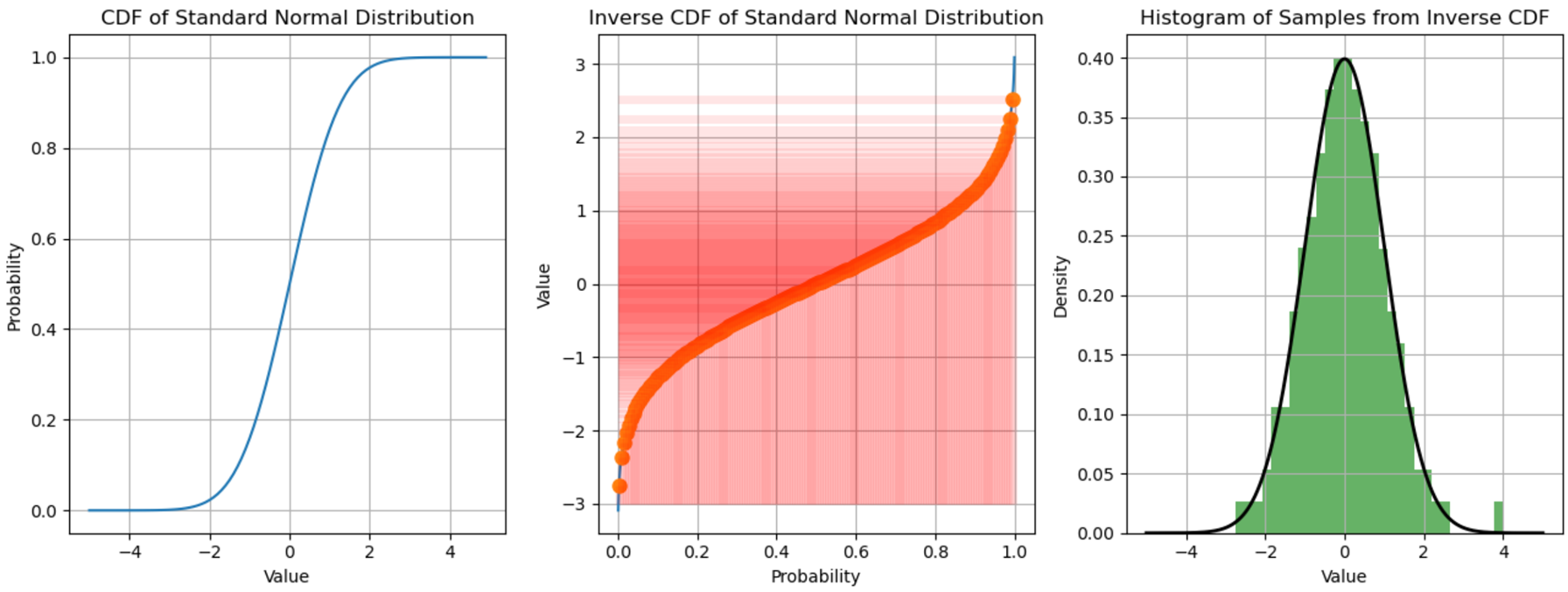
sample의 histogram이 완전히 가우시안 분포를 따르는 것을 볼 수 있다.
즉, 정리하면, sampling이란 본래 목표로하는 함수의 ICDF를 구한다음 확률 값을 넣었을 때의 output이다. 그러나 우리가 target으로 하는 분포(사람, 개 , 고양이등)는 매우 복잡하기에 CDF, ICDF를 계산하기 매우 어렵다. ICDF를 구하지 않고 sampling을 하는 여러 방법이 있는데, 그 중 제일 많이 사용되는 것은 단연코 Monte Carlo Marcov Chain(MCMC)일 것이다. 대표적으로 Metropolis-Hasting sampling, Rejection Sampling이 존재한다.

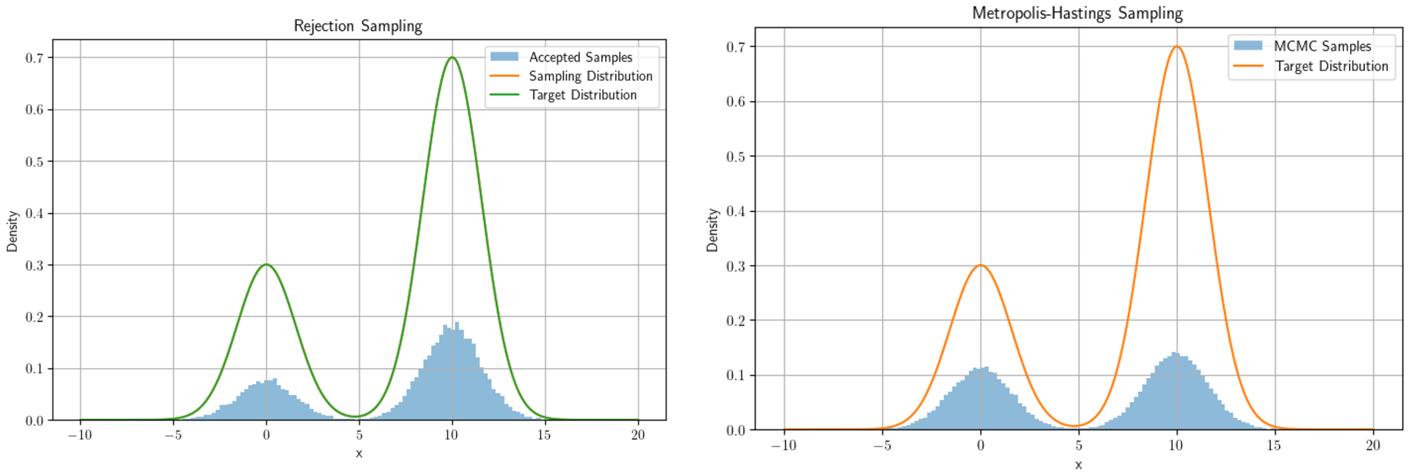
코드 , 내용 참조

결국 생성 모델(Generative model)이라는 것은 Target 분포의 ICDF또는 Quantile Function을 근사하는 것이라고 볼 수 있다. (이를 극대화 한 것이 Flow-based 모델이라고 한다.)

Evidence

위에서 언급한 생성 모델을 정의하면, 목적은 true distribution $p(x)$와 우리의 model $q_\phi(x)$가 같았으면 좋겠다. 즉, $p(x) \approx q_\phi(x)$을 성립하는 model $q_\phi(x)$를 구하는 것이다. VAE논문을 보면 Evidence Lower Bound라는 개념이 나온다.(cs229에서도 나온다. 즉 여러 곳에서 쓰임) Lower bound는 알겠는데, Evidence라는 말은 무엇일까? 목적을 다시 상기해보면, 우리는 $p(x;\theta)$를 모델링을 하고 싶다. 이때, true distribution $p(x)$는 $x$가 존재할 확률이라고 볼 수 있고, 이는 $x$가 존재할 증거(evidence)라고 부를 수 있다.
즉, Evidence라는 말을 쓰는 것은 확률 값을 어떠한 값이 존재할 증거로 바라보겠다는 관점이다. 여기서 target분포와의 차별점을 두기 위해서 그리고 연산의 간단성을 위해서 log를 씌워준 값 $\log p(x)$를 Evidence라고 부른다.
이를 정리하면 다음과 같다.

여기서 score라는 개념이 나오는데, 이는 지난 포스팅을 참조해주길 바란다. 여기선 간략하게 설명하면, 목표로 하는 분포의 방향(gradient)를 의미한다고 생각하면 된다.

이제부턴 연산의 간단성을 위해서 Evidence $\log p(x)$를 구하는 것을 목표로 해보자. ELBO란 다음과 같은 수식을 의미한다.

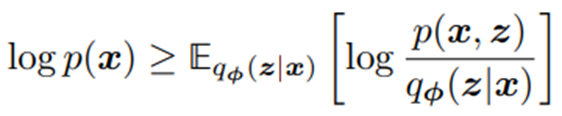
여기서 확률의 중요한 2개의 성질을 사용하여 ELBO를 유도해보자.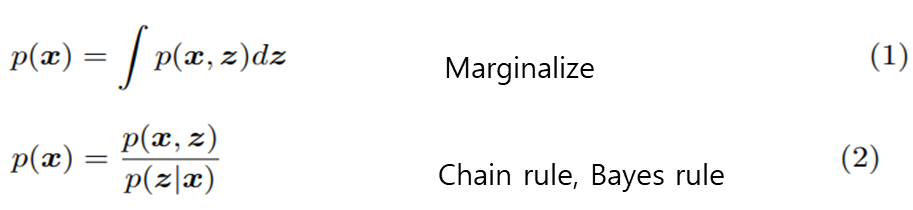

---

Marginalize

ELBO를 유도할 때의 핵심은 $1=\frac{q_\phi(z|x)}{q_\phi(z|x)}$ 를 사용하는 것이다. 이때 (7) ->(8)에서 Jensen's inequality란 무엇인가?

Jensen's inequality

어떠한 함수의 이계도함수(두번 미분한 함수) $f''(x)\geq0$ 하다면 그 함수는 convex라고 정의하고, $f''(x)\leq0$하다면 concave라고 정의한다. 즉, 간단하게 표현해보면 Convex와 concave는 밑의 그림처럼 표현할 수 있다.

이때 함수가 Convex하다면, 모든 $x_1,x_2$에 대하여 다음과 같은 함수의 성질을 만족한다. (concave라면 부등호가 반대이다)

이를 그림으로 보면 다음과 같다.

$f(\lambda x_1 +(1-\lambda)x_2\leq \lambda f(x_1)+ (1-\lambda)f(x_2))$를 $x_1, x_2$뿐만이 아니라 모든 Random Variable X에 대해서 다시금 정리하면 $\mathbb{E}[f(X)]\geq f(\mathbb{E}[X])$로 표현할 수 있다.
이때의 $\mathbb{E}[f(X)]\geq f(\mathbb{E}[X])$를 Jensen's inequality 라고 부르며, 이를 정리하면 다음과 같다.

convex : $\mathbb{E}[f(X)]\geq f(\mathbb{E}[X])$

concave: $\mathbb{E}[f(X)]\leq f(\mathbb{E}[X])$

그러나 ELBO는 Jensen's inequality를 사용하면 쉽게 유도할 수 있지만, ELBO가 무슨 의미인지는 사실 직관적으로 와닫지는 않는다. 또 다른 방식은 Chain rule 방식으로 유도를 해보자.

Chain rule

마찬가지로 $1=\frac{q_\phi(z|x)}{q_\phi(z|x)}$를 사용하는데, Marginalize와는 다르게 $D_{KL}$ 생긴 것을 볼 수 있다. 여기서 KL Divergece는 항상 0보다 크거나 같아야 하므로, (16)번째 수식이 유도되는 것을 볼 수 있다.
여기서 $D_{KL}(q_\phi(z|x)\; || \;p(z|x))$가 의미하는 것을 생각해보면, $q_\phi(z|x)$는 우리의 모델이고, $p(z|x)$ True posterior이다.

즉, $x$를 condition으로 주어졌을 때, latent vector $z$를 output으로 하는 모델 $q_\phi(z|x)$와 $p(z|x)$의 분포가 같아지기를 원한다. 그러나 $p(z|x)$는 구할 수 없는 분포이기에, ELBO인 $\mathbb{E}_{q_\phi(z|x)}[\log \frac{p(x,z)}{q_\phi(z|x)}]$를 Lower bound로 줌으로서, $\log p(x)$를 근사하려고 하는것.

여기까지만 알아도 사실 ELBO를 쓰는 이유에 대해서 알 수 있지만, 명확하게 해석이 되지는 않는다. ELBO를 줄이는 것이 과연 $\mathbb{E}_{q_\phi(z|x)}[\log \frac{p(x,z)}{q_\phi(z|x)}]+ D_{KL}(q_\phi(z|x)\; || \;p(z|x))$를 줄이는 것에 도움이 될까? 이는 ELBO를 좀 더 자세히 뜯어보면 알 수 있다.

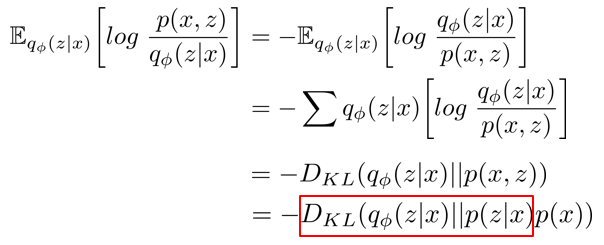
ELBO를 전개하면 결국 ELBO에 $D_{KL}(q_\phi(z|x)\; || \;p(z|x))$ term이 들어있는 것을 확인할 수 있다!
위에서 언급하였듯, KL Divergence는 항상 0보다 크기 때문에, KL Divergence가 줄어들 수록, ELBO는 커지는 것을 알 수 있다.(-가 붙어있으므로) 즉,

Maximize ELBO = Minimize KL Divergence

이 성립한다. (kL divergence가 항상 0보다 크기에, ELBO는 항상 0보다 작다)
결국 ELBO를 줄이는 것(0에 가까워 지는 것이)이 $D_{KL}(q_\phi(z|x)\; || \;p(z|x))$도 줄이는 것이라는 것을 알 수 있고, Evidence Lower Bound라고 부르는 이유를 알 수 있게되었다.
직접적으로, Maximize ELBO를 하는 방식을 Variational이라고 부른다.

A separate meaning of ELBO

ELBO를 다른 방식으로 자세하게 뜯어보자. Chain rule을 사용하여 ELBO를 전개해보면,

ELBO는 reconstruction term과 prior matching term으로 나눌 수 있게 되는데, 여기서 $\phi, \theta$는 learnable parameter이다.
각각의 의미를 살펴보면,

• reconstruction term: model $q$와 또다른 model $p$에 대한 식이고
• prior matching term: model $q$와 prior(latent vector) distribution $p(z)$에 대한 식으로 볼 수 있다.

prior matching term은 사실 직관적으로 우리의 모델이 true prior distribution $p(z)$와 비슷해지기를 원한다는 것을 알 수 있지만, reconstruction term 은 어떤 의미를 가질까?

reconstruction term을 자세히 살펴보면, 결국 -가 곱해진 Cross Entropy임을 알 수 있다.
여기서 model $q$와 model $p$를 각각 Encoder ($q_\phi(z|x)$) , Decoder ($p_\theta (x|z))$라고 부른다.
이런 식의 구조를 우리는 AutoEncoder라고 부른다. 그림으로 쉽게 보자.

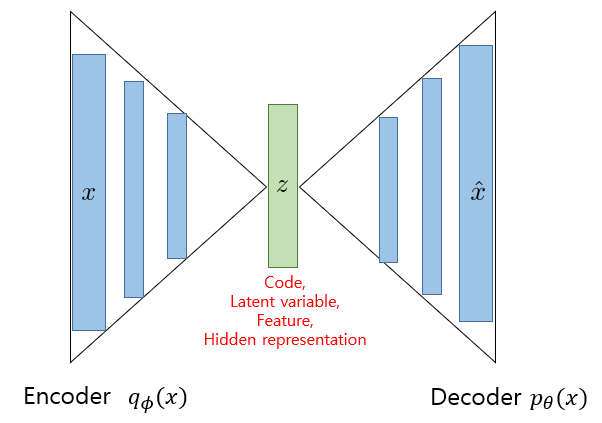
정리하면, reconstruction term은 Encoder과 Decoder가 서로 비슷해지기를 원하는 항인 것이고,
prior matching term은 Encoder의 output이 실제 true prior distribution $p(z)$가 비슷해지기를 원하는 항이다.

• 직관적으로 생각해보자. AutoEncoder란 결국 input x를 얼마나 잘 압축하고, 정보의 손실 없이 얼마나 잘 복원하는가? 를 학습하는 모델이다.
  선형 대수관점으로
  $z = Ax$ 라고 할때, $\hat x \approx x$가 되는 가장 완벽한 방법은 $\hat x = A^{-1}z$가 될 것이다. 이 개념을 사용한 것이 Flow-based model이고, VAE는 Decoder가 꼭 Encoder의 역방향일 필요는 없지만, 두 분포가 비슷하다면, 압축과 복원을 잘 할 수 있을 것이다를 모델링 하는 것이다.

VAE

여기서 조금만 더 나아가서, ELBO를 Objective function으로 두고, Encoder ($p_\theta (z|x))$의 output 즉, $p(z)$ 다변량 가우시안이라고 가정한 모델이 바로 Variational AutoEncoder(VAE)이다. 수식으로 전개하면,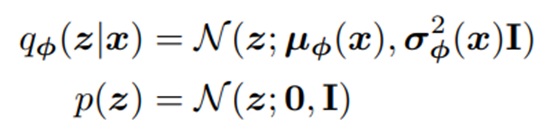
이에 따른 목적함수는 다음과 같다.

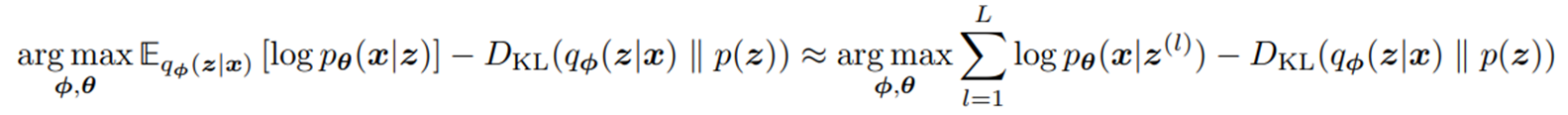
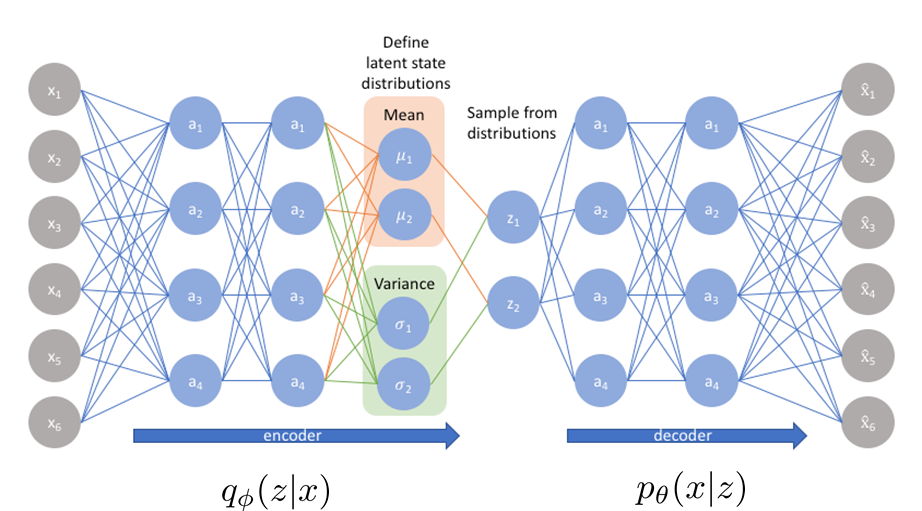
여기서 Encoder ($q_\phi(z|x)$)의 output $z$는 random variable이기에 미분이 불가능하고, SGD가 안된다는 단점이 있다. 이를 해결하기 위해서 random varariable $z$를 noise에 대하여 식을 전개하여 정리한 것을 Reparameterization trick이라고 부른다.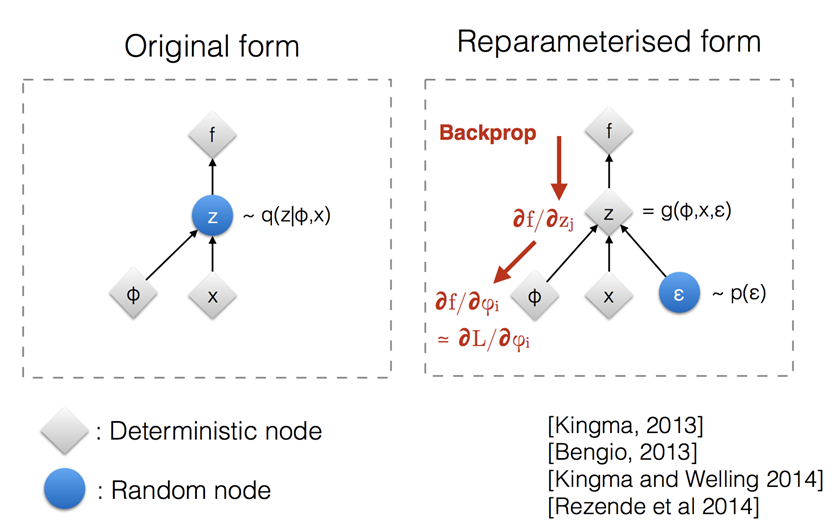
참고, VAE 정리 포스트