Comment

Diffusion model을 알기 위해선 VAE에 대해서 자세하게 알 필요가 있다. VAE를 읽고 수식적인 부분만 집중적으로 증명하려고 한다.

Summary

VAE의 목적은 VB(Variational Bayesian) 접근으로 intractable posterior를 근사하는것
AutoEncoding VB(AEVB)알고리즘으로 SGVB(stochastic gradient VB)로 효율적으로 추정하는것
MCMC(Markov Chain Monte Carlo)같은 반복적이고 계산 비용이 높은 방법을 사용하지 않고 approximation하는 것을 목표로 함.
SGVB를 사용하는 method중, recognition model의 경우 Variational auto encoder(VAE)라고 부른다

notation & 용어 정리

VB: Variational Bayesian
SGVB: Stochastic Gradient variational Bayesian
MCMC: Markov Chain Monte Carlo

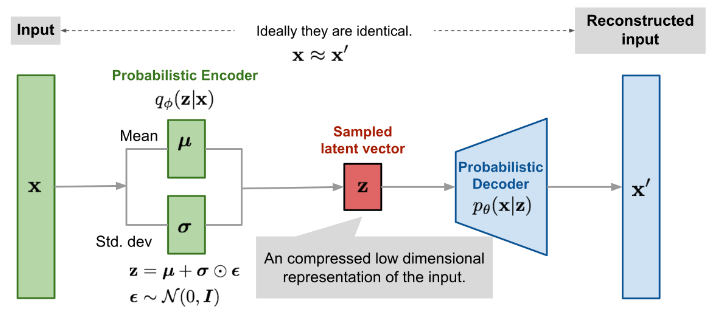
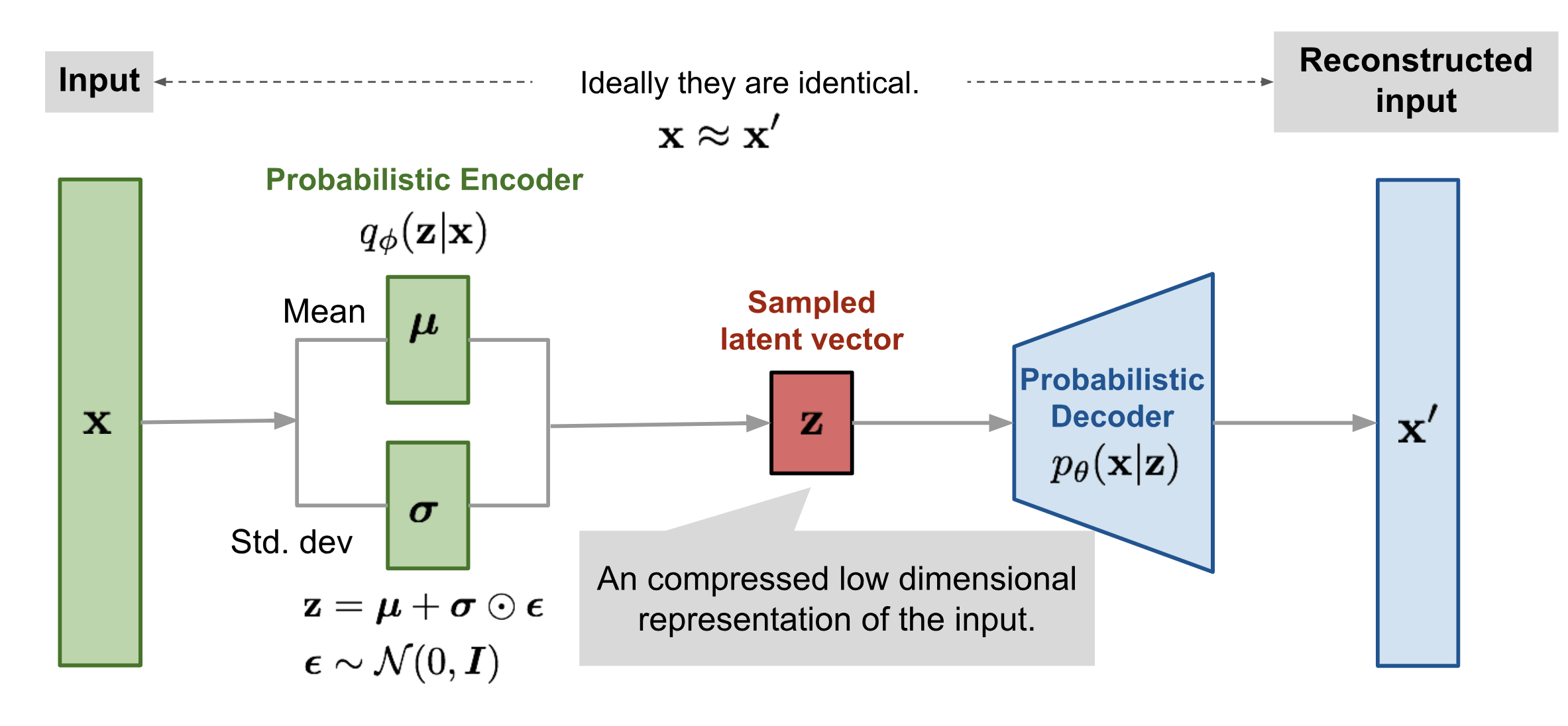
• 전체적인 구조는 위의 AEVB를 따른다.

notation for VAE

Encoder

$g_\phi(.)$: Encoding function parameterized by $\phi$
$q_{\phi}(z|x)$: Probabilistic encoder

---

Decoder

$f_{\theta}(.)$: Decoding function parameterized by
$p_{\theta}(x|z)$ : Probabilistic decoder (Likelihood distribution)

Define

$p_{\theta}(z) = \mathcal{N}(z;0,1)$ : prior distribution
$p_{\theta}(z|x)$ : true posterior
$p_{\theta}(x|z)$ : likelihood
$p_{\theta}(x,z) = p(x|z)p(z)$: Maximum a posterior (posterior of generative(decoder))

Method

기본적인 전략은 lower bound estimator를 미분하여 gradient descent를 진행하는 것. ML(Maximum likelihood)와 MAP(Maximum a Posterior)를 사용하여 (global) parameters를 찾아내는 것이다.

Problem Scenario

lower bound를 설정하기 위해서 논문에서는 몇가지 시나리오를 가정한다.

1. $X = \{x^{(i)}\}_{i=1}^N$: Dataset은 i.i.d를 따른다고 가정. 여기서 variable $x$는 continuous or discrete variable이다.
2. data가 unobserved continuous random variable $z$에 의해서 어떤 random process에 의해 생성된다고 가정한다.

process는 2 step을 따르는데,

1) value $z^{(i)}$는 어떤 prior distribution $p_{\theta^*}(z)$에 의해서 생성된다.
2) value $x^{(i)}$는 어떤 conditional distribution $p_{\theta^*}(x|z)$로부터 생성된다.

$p_{\theta^*}(z)$ 와 likelihood $p_{\theta^*}(x|z)$는 parametric families(하나 이상의 파라미터에 의해 제어되는 특정 형태의 확률분포를 가진 모델들의 집합) $p_\theta(z),p_\theta(x|z)$로 부터 형성되고, PDF는 대부분의 $\theta, z$에 대해 미분이 가능하다고 가정한다(gradient decent)를 진행하기 위함

중요한 점은 marginal or posterior probabilities에 대해서 common assumption을 하지 않고 general algorithm을 제시한다고 한다.

문제점

1. Intractability, marginal likelihood $p_{\theta}(x)$는 intractable(구하기 어려움) 그래서 EM 알고리즘 같은 방법을 사용 x (MLE, MAP같은 추정이 아닌 직접적인 PDF계산이 어렵다는 것을 의미한다)
   2: Large dataset: Dataset이 너무 크기에 small minibatches를 진행하고 싶어한다.

이에 대한 해결법으로
1. parameter $\theta$에 대해서 ML or MAP로 근사
2. latent variable z에 대해 poseterior을 근사하도록 함
3. 변수 x에 대해서 Efficient approximate marginal inference가 가능하게끔 한다. (모든 종류의 inference는 x에 대한 prior이 요구된다고 함) ,ex image denoising, inpainting and super-resolution

이러한 시나리오와 방법을 제시하였을 때, 위의 notation에서 정리한 것 처럼 recognition model(encoder)를 $q_\phi(z|x)$ , intractable true posterior(decoder) $p_{\theta}(z|x)$로 정의한다.

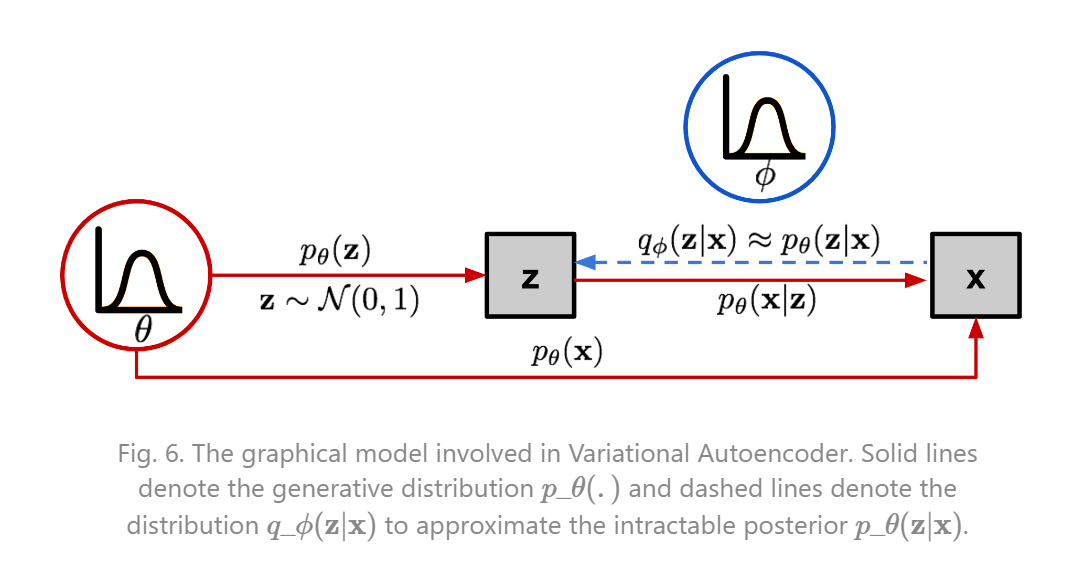
위에서 정의한 recognition model과 true posterior의 관계는 그림처럼 설명이 가능하다. 우리는 recognition model이 true posterior과 비슷해지기를 희망한다.

• coding theory 관점에서 관찰되지 않은 변수 $z$는 latent representation 혹은 code라는 관점으로 볼 수 있다고 한다.

• 여기서 posterior이 intractable하기에 논문에서는 ELBO라는 방법을 소개한다.

Variational bound

논문에서 나온 수식의 흐름대로 ELBO를 이해해보자.
위에서 random process를 다시한번 가지고 와 보면 ,

---

process는 2 step을 따르는데,

1) value $z^{(i)} \sim p_{\theta^*}(z)$
2) value $x^{(i)}\sim p_{\theta^*}(x|z)$

---

라는 process를 따른다. 여기서 VAE의 최종 목적은 latent vector $z$를 넣었을 때, $\hat x \approx x$이다. 이를 정리해보면
우리의 모델 $p_\theta()$에서 x가 나올 확률은 $p_{\theta}(x^{(i)}) = \int p_{\theta}(x^{(i)}|z)p_{\theta}(z)dz$이다. (이해가 안가면 그림을 다시한번 보자)

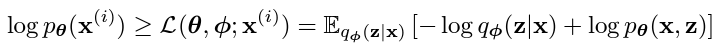
모든 데이터 샘플에 대해서 나올 확률은 다음과 같은데,$p_\theta(x^{(1)},x^{(2)},\cdots,x^{(n)})$
이를 log Likelihood로 표현하면
$\theta^* = \underset{\theta}{\textrm{argmax}}\;\textrm{log} \;p_\theta(x^{(1)},x^{(2)},\cdots,x^{(n)})$
$= \underset{\theta}{\textrm{argmax}}\;\textrm{log} \;\underset{i=1}{\overset{N}{\sum}}\;\textrm{log}\;p_{\theta}(x^{(i)})$
이를 marginal likelihood 라고 한다.
여기서 $\textrm{log}p_{\theta}(x^{(i)})$를 주목해서 봐보자. VAE는 encoder $q_{\phi}(x|z)$와 decoder $p_\theta(z|x)$로 구성되어있다. log likelihood $p_{\theta}(x)$를 encoder와 decoder로 표현하기 위해서 트릭이 필요한데, 다음과 같다.

---

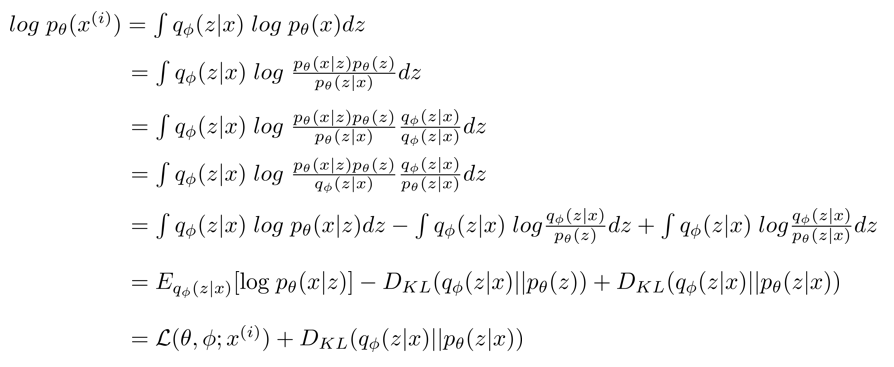
여기서 $\frac{q_\phi(z|x)}{q_\phi(z|x)}$ term을 넣어 준 것이 굉장히 인상적이다.
$D_{KL}(q_\phi(z|x)||p_\theta(z|x))$는 encoder $q_\phi(z|x)$ 와 Posterior $p_\theta(z|x)$인데 둘다 $x$가 주어진 posterior로 이해할 수 있다.

---

결국 정리하면, log likelihood $\theta^* = \underset{\theta}{\textrm{argmax}}\;\mathcal{L}(\theta,\phi;x^{(i)})+D_{KL}(q_\phi(z|x)||p_\theta(z|x))$인데
KL - divergence의 오른쪽 확률은 posterior로 실제로 구할 수 없는 값이다.

$p_{\theta}(z) = \mathcal{N}(z;0,1)$ : prior distribution
$p_{\theta}(z|x)$ : true posterior
$p_{\theta}(x|z)$ : likelihood $

이에 논문에서는 Evidence Lower bound를 사용하는데, 마지막 식만 다시 가지고 와 보면

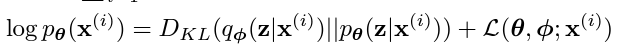
로 정의할 수 있다. 여기서 $D_{KL}$를 이항하여 다시 정리하면

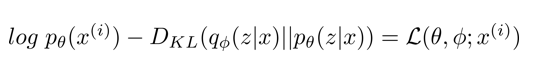
$D_{KL}$항은 실제로 계산할 수 없지만, 0에 가까워 지거나 0보다 크다면(positive semi definite하다면) 최소한 $log p_{\theta}(x^{(i)}) \geq \mathcal{L}(\theta,\phi;x^{(i)})$라는 것을 알 수 있다.
즉,

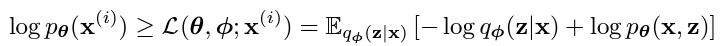
이 성립한다. 이는 곧 $\mathcal{L}(\theta,\phi;x^{(i)})$가 커진다면 확률 likelihood $\textrm{log}\; p_{\theta}(x^{(i)})$도 커짐을 의미하며, 근사치인 최소한의 bound $\mathcal{L}$을 Evidence lower bound라고 정의한다.

SGVB

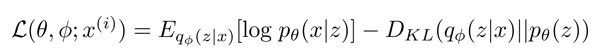
ELBO를 이제 미분하여 구하면 되는데, 문제점이

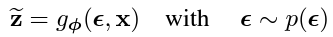
아까의 process를 다시 상기해보면

1) value $z^{(i)} \sim p_{\theta^*}(z)$

z가 random성을 띈다는 것이다.이는 함수의 미분을 통한 backpropagation이 진행되지 않음을 의미한다. 이를 MCMC같은 방법으로 해결 할 수 있지만

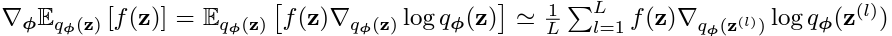
이는 계산의 복잡성이 크기에 별로 좋지 않다.

이를 해결하기 위해서 다음 트릭을 사용한다.

reparametrization trick

$\tilde z \sim q_{\phi}(z|x)= N(\tilde z;\mu,\sigma^2I)$가 의미하는 것은 $\tilde z$가 $q_{\phi}$로 부터 sampling되는 데이터라고 했을 때, z는 sampling되는 data이기 때문에 gradient를 사용한 backpropagation을 사용할 수 없다. 이를 $\theta$에 대해서 바라보는 것을 reparametrization trick이라고 부른다. 이를 식으로 표현해보면, $\tilde z=g_{\phi}(\epsilon,x)= \mu+\sigma^2\odot\epsilon$ ,where $\epsilon \sim p(\epsilon)$으로 표현할 수 있다. $\tilde z$가 sampling data에서 random variable $\epsilon$에 대한 function으로 변하였다.

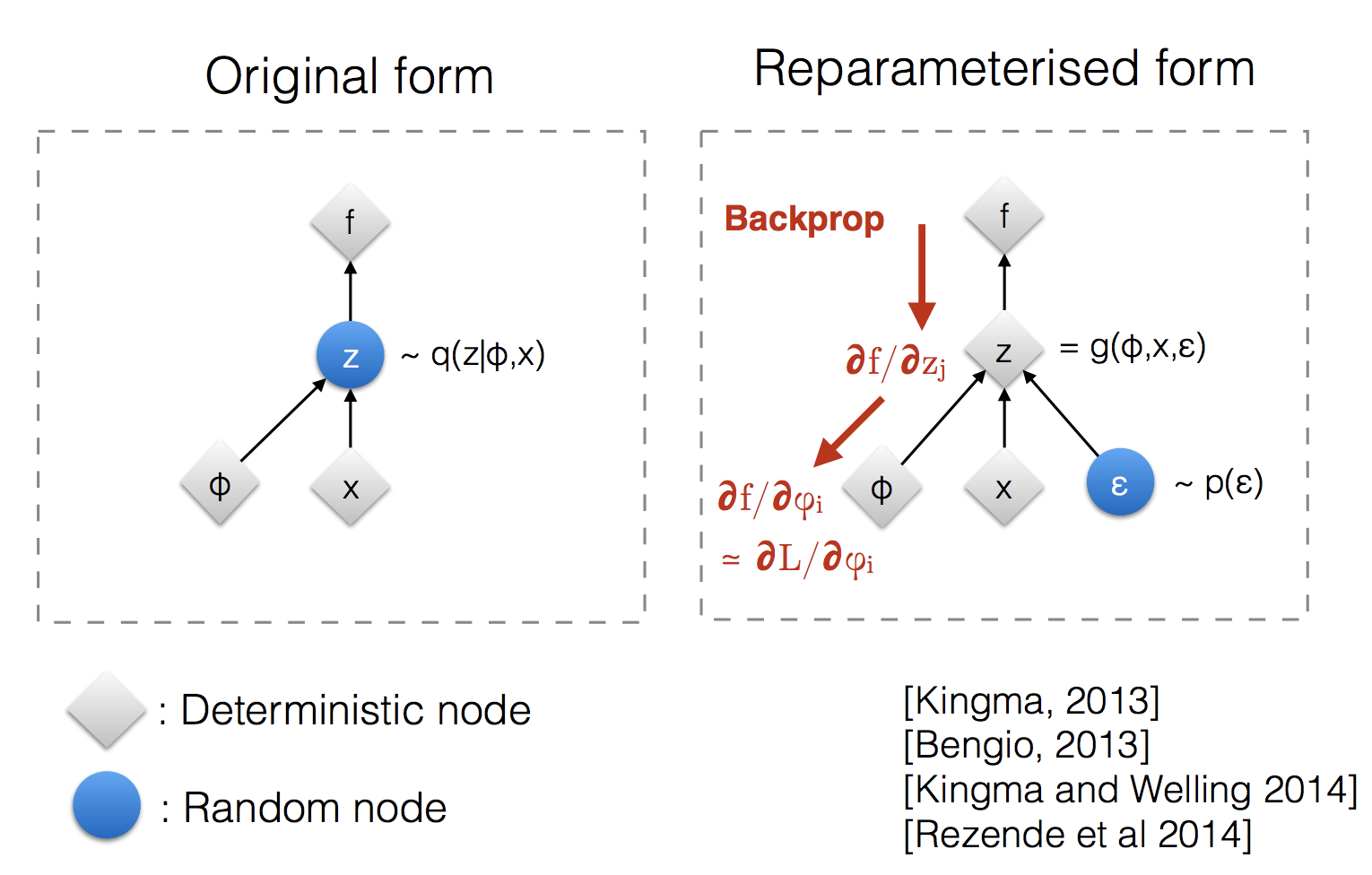
결국 reparametrization trick란 sampling의 random성을 없애기 위해 random variable을 변수로 바라보는 것이고, 미분이 가능하게 하는 것이다.
$z = \mu + \sigma \epsilon$: 여기서 $\mu$는 distribution의 location, $\sigma$는 scale $\epsilon$은 noise로 생각하면 된다.

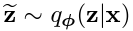
다음과 같은 sampling을 reparametrization trick를 사용하여 다음과 같이 표기할 수 있는데, 여기서 $\epsilon$이 random variable이 되게 된다.

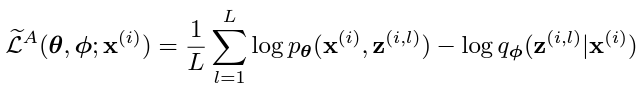
이 방법을 사용하여 ELBO를 새롭게 정의하면

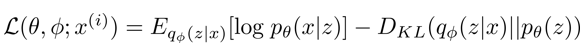
로 표현할 수 있다.

Variational Auto Encoder에 대해서 reparametrization trick을 사용하여 바라보면 다음과 같이 정리할 수 있다.
Encoder를 reparametrization trick을 사용하여 표현하면 다음과 같은데,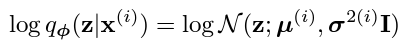
즉, 인코더는 i 샘플에 대하여 $\mu$, diagonal $\sigma^2$를 output으로 하는, 즉, x에 해당하는 가우시안 분포를 생성하는 역활을 한다.

Loss

VAE의 ELBO MLE는 다음과 같았다. 여기서 각 항마다 의미를 가지는데,

첫 번째 항은 $\mathbb{E}_{q_{\phi}(z|x)}[\textrm{log}\;p_{\theta}(x|z)] = \int q_{\phi}(z|x)\;log \;p_\theta(x|z)dz$로서 이는 사실 encoder와 decoder의 negative cross entropy와 같다.
첫 번째 항은 encoder와 decoder가 autoencoder처럼 reconstruction을 잘 할 수 있게 도와주는 error이기에 reconstruction error라고 한다.
두 번째 항은 prior distribution $p_{\theta}$와 (encoder)x에 대한 posterior $q_{\phi}(z|x)$의 차이를 줄여주므로, regularization error라고 한다.

참조

1.
2.