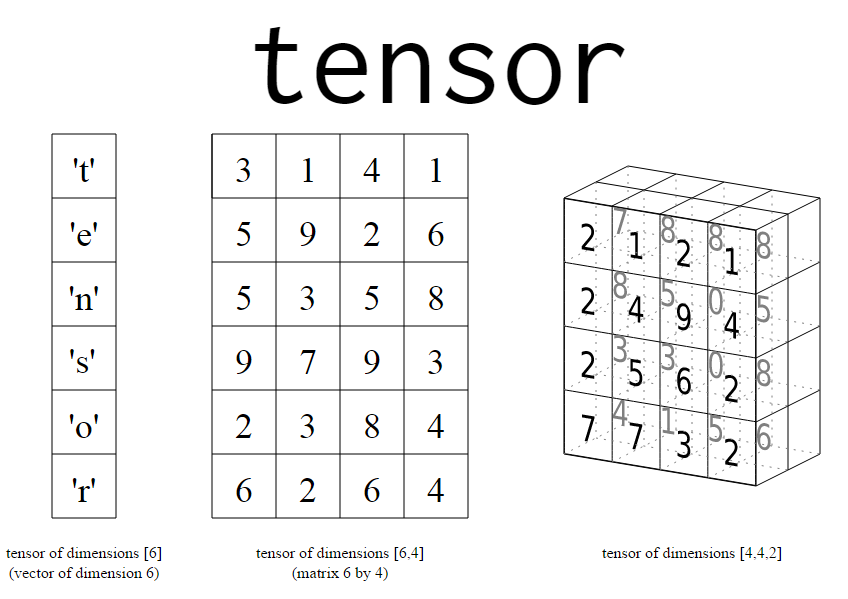
개요
torch.sum()을 사용하는데, 2차원을 넘어가면 계속해서 헷갈리다가, 어렵게 이해를 했다. 이해한 것을 토대로 정리해보려고 한다.
사용법
torch.sum(data)
사용법 자체는 numpy의 numpy.sum()과 다르지 않다.
a= torch.arange(4*4).view(4,4) print(a)a가 밑처럼 생긴 4x4의 matrix라고 할 때,
tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]])torch.sum(a)a를 dim없이 sum()하면
tensor(120)matrix의 모든 값을 더한 120이 나온다.
2차원에서 torch.sum(data,dim)
그렇다면 data에 dim(axis로 써도 된다.)을 사용하면 어떻게 될까?
print(torch.sum(a,axis=0),torch.sum(a,axis=0).shape) print(torch.sum(a,dim =1),torch.sum(a,axis=0).shape) print(torch.sum(a,1)) # dim,axis를 쓰지 않아도 결과가 나옴을 보여준다.tensor([24, 28, 32, 36]) torch.Size([4]) tensor([ 6, 22, 38, 54]) torch.Size([4]) tensor([ 6, 22, 38, 54])
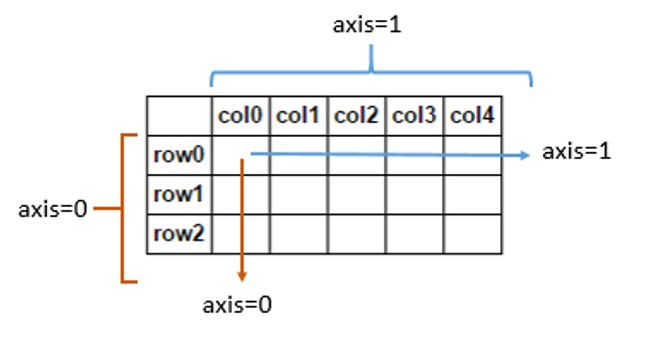
axis =0이라는것은 column을 기준으로 더한 것이기 때문에,tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]])위의 matrix를 column을 기준으로 더한 [24,28,32,36]이 나왔다.
ex) 24 = a[0][0]+ a[1][0]+a[2][0]+a[3][0]
axis=1(dim=1)을 하면 그림처럼 row들 끼리 계산을 하기 때문에, [6,22,38,54]가 나온 것을 확인 할 수 있다.
6 = a[0][0]+ a[1][0]+ a[2][0]+ a[3][0]
3차원 이상에서의 계산
시도
그렇다면 3차원에서의 torch.sum()은 어떻게 작용되는가?
2x3x4의 배열을 생성해보자.x = torch.arange(2*3*4).view(2,3,4) print(x)tensor([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]])3x4크기의 matrix가 2개 생성된 것을 확인 할 수 있다.
그럼 2차원일 때 처럼 axis=0을 넣고 계산해보자.torch.sum(x,0)tensor([[12, 14, 16, 18], [20, 22, 24, 26], [28, 30, 32, 34]])뭔가 생각했던 계산이 나오지 않았다. 처음에 axis=0으로 넣었을 때 필자는 column들끼리 계산인
tensor([[12, 15, 18, 21], [48, 51, 54, 57]])가 나와야 한다고 생각했었다. 2차원에서는 분명 column들끼리 계산된 것이 왜 예상과 다르게 나온 것일까?
torch.sum(x,0)의 결과를 보면 3x4크기의 한개의 matrix가 된 것을 볼 수 있다. 더욱 주의 깊게 보면, x[0]의 matrix와 x[1]matrix가 서로 더해진 것을 확인해 볼수 있다.
직관적으로 보면 이렇게 생겼다.
[0,1,2,3], [12,13,14,15], [12,14,16,18], [4,5,6,7], + [16,17,18,19], = [20,22,24,26], [8,9,10,11], [20,21,22,23], [28,30,32,34]
차원으로서의 접근
그렇다면 torch.sum(x,0)을 0번째 인덱스의 차원 이라고 생각해보면 어떨까?
우리가 만든 x는 3x4의 행렬이 2개 존재하는 3차원이다.
(2,3,4)를 차원이라고 생각하면 3차원이 2 , 2차원이 3, 1차원이 4로서.
즉 0번째 인덱스가 2 , 1번째 인덱스가 3, 2번째 인덱스가 4가 된다.
- 그럼 axis=1인 계산을 해보고 싶으면 어떻게 해야겠는가?
torch.sum(x,1)tensor([[12, 15, 18, 21], [48, 51, 54, 57]])axis =1 즉 row들끼리의 합을 구하고 싶으면 2차원 즉 x[1]차원을 dim에다가 넣어주면 됬던 것이다.
정리
axis(dim)을 방향이 아닌 차원의 인덱스로 접근하는 것.
이는 2차원 이상의 모든 sum()을 접근할 때 유용하게 쓰인다.arr = torch.arange(2*3*4*5).view(2,3,4,5) print(arr, arr.shape)tensor([[[[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [ 10, 11, 12, 13, 14], [ 15, 16, 17, 18, 19]], [[ 20, 21, 22, 23, 24], [ 25, 26, 27, 28, 29], [ 30, 31, 32, 33, 34], [ 35, 36, 37, 38, 39]], [[ 40, 41, 42, 43, 44], [ 45, 46, 47, 48, 49], [ 50, 51, 52, 53, 54], [ 55, 56, 57, 58, 59]]], [[[ 60, 61, 62, 63, 64], [ 65, 66, 67, 68, 69], [ 70, 71, 72, 73, 74], [ 75, 76, 77, 78, 79]], [[ 80, 81, 82, 83, 84], [ 85, 86, 87, 88, 89], [ 90, 91, 92, 93, 94], [ 95, 96, 97, 98, 99]], [[100, 101, 102, 103, 104], [105, 106, 107, 108, 109], [110, 111, 112, 113, 114], [115, 116, 117, 118, 119]]]]) torch.Size([2, 3, 4, 5])(2x3x4x5)크기의 4차원 arr의 2차원을 더하고 싶을 때
print(torch.sum(arr,2),torch.sum(arr,2).shape)tensor([[[ 30, 34, 38, 42, 46], [110, 114, 118, 122, 126], [190, 194, 198, 202, 206]], [[270, 274, 278, 282, 286], [350, 354, 358, 362, 366], [430, 434, 438, 442, 446]]]) torch.Size([2, 3, 5])sum(arr,dim=2)로 더하고 싶은 차원의 index를 넣어주니 잘 작용된것을 확인 할 수 있다.
※ 번외: dim에도 tuple형태로 2차원 이상을 넣을 수 있다.
arr = torch.arange(2*3*4*5).view(2,3,4,5) print(torch.sum(arr,0), torch.sum(arr,2).shape) print(torch.sum(arr,(2,1)),torch.sum(arr,(2,1)).shape,"\n") print(torch.sum(arr,(3,2,1)),torch.sum(arr,(3,2,1)).shape,"\n")tensor([[[ 60, 62, 64, 66, 68], [ 70, 72, 74, 76, 78], [ 80, 82, 84, 86, 88], [ 90, 92, 94, 96, 98]], [[100, 102, 104, 106, 108], [110, 112, 114, 116, 118], [120, 122, 124, 126, 128], [130, 132, 134, 136, 138]], [[140, 142, 144, 146, 148], [150, 152, 154, 156, 158], [160, 162, 164, 166, 168], [170, 172, 174, 176, 178]]]) torch.Size([2, 3, 5]) tensor([[ 330, 342, 354, 366, 378], [1050, 1062, 1074, 1086, 1098]]) torch.Size([2, 5]) tensor([1770, 5370]) torch.Size([2])
- 계산은 선두 인덱스부터 한다고 생각하면 된다.
torch.sum(arr,(2,1))의 경우 [2] 즉 row를 먼저 계산하고, [1] 3차원을 계산한것과 같다.
torch.sum(arr,(1,2))와 계산 결과는 같다.