논문 저자의 정리

summary

---

• Score matching for score estimation 이란 generative model $S_{\theta} \approx \nabla_xlog p_{\theta}(x)$가 되게끔 하는 model이다.

• sampling을 하기 위해서 Langevin dynamics를 사용하여 sampling을 진행하는데, 기존의 langevin dynamics는 low density pdf에서는 sampling이 잘 되지 않는 문제가 발생.

• 이를 해결하고자 본 논문에서는 Annealed Langevindy namics를 사용하여 기존의 low density 문제를 해결

• Annealed Langevin dynamic란 score function $S(\theta)$에 variable 로서 $\sigma$를 추가하여 time-step에 따른 sigma를 조절하는 방식이다.

---

background

Energy based model(EBM)
에너지 기반 모델(Energy-Based Model, EBM)에서 "에너지"는 데이터의 상태 또는 구성에 대한 스칼라 값

에너지란, 모델이 얼마나 그 데이터 상태를 선호하는지를 나타내는 척도로

에너지가 낮을수록 모델은 해당 상태를 더 선호하며, 이는 해당 상태가 더 높은 확률을 가지게 됨을 의미한다.

사실 말로만 들었을 땐 무슨 말인지 이해가 잘 가지 않는다. 확률 모델과 비교를 해보자.

• EBM: 확률적 모델링 model로서, 데이터의 확률 분포를 모델링 하는데 사용한다.
  $F:\mathcal{X}\rightarrow \mathcal{Y}$로 표현할 수 있으며, $F(x,y)$ x,y 사이의 dependency로 표현할 수 있다. EBM의 목표는 $\check y = \underset{y}{\textrm{argmin}}\;F(x,y)$로 표현할 수 있다.
  MLE의 $p(y|x)$ 처럼 $x$에 대해 $y$를 분류하기 보단 $(x,y)$의 짝이 맞는지를 예측하는 것이 주 목적이라고 생각할 수 있겠다. Ex): $y$가 $x$의 고해상도 이미지 인가? or $y$가 $x$의 좋은 번역문인가?
  보통 함수로는 $p(x) = \frac{e^{-E(x)}}{Z}$로 표현할 수 있으며, 여기서 $E(x)$가 에너지 함수이다.

• EBM은 $p(x) = \frac{e^{-E(x)}}{Z}$ 형태로 되어있는데, 여기서 exponential 연산을 함으로써, Energy function의 음수 값을 양수로 바꿔주는 역활도 한다.
  

다음은 EBM의 예시들이다.

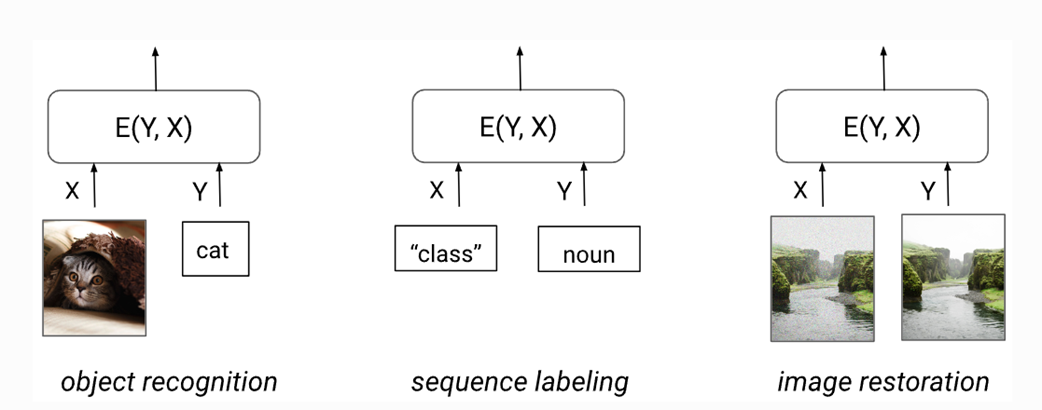
EBM의 기본 아이디어는 에너지 함수를 학습하여 데이터의 복잡한 분포를 모델링하는 것이라고 한다.
이 에너지 함수는 일반적으로 신경망으로 표현되며, 이 신경망의 가중치는 학습 과정에서 최적화 될 수 있다고 한다.
EBM의 확률 분포는 $p(x) = \frac{e^{-E(x)}}{Z}$ where $Z \sim \int_x e^{-E(x)dx}$로 표현 된다고 한다.

Generative model에서 EBM을 쓰는 이유는 크게 4가지가 있는데,
1) Representation : $E(x)$를 Neural Network로 사용할 수 있다.
2) Flexibility : 다양한 형태의 데이터에 적용 가능함/
3) Learning method: gradient descent가 가능하다고 한다.
4) Unsupervised learning : data feature에 complexity를 포착할 수 있기 때문.
참고

---

introduction

생성 모델은 최근 2개의 방법으로 나뉘는데
1) Likelihood-based models

log-likelihood 또는 다른 적합한 방법을 training시키는 방식이고,

2) Generative Adversarial Networks(GAN)으로 나뉨

데이터 분포와 모델의 분포 사이의 f-divergences 또는 integral probability metrics을 최소화 시키는 방식으로 작동한다.

• f-divergence: $D_F(P//Q)) = \int p(x) F(\frac{q(x)}{p(x)})dx$ where $q(x),p(x)$ distribution.
  $F(x)$는 divergence function으로 예를 들어 Kullback -Leibler , Jensen-shanon, Hellinger distance등이 있다고 한다.

---

• Integral Probability metrics : 두 분포의 차이를 측정함 (CDF를 사용)
  $IPM(P,Q)= \underset{f\in F}{\textrm{sup}}|E_{x\sim P}[f(x)]-E_{x\sim Q}[f(x)]|$

---

(stein) Score : 확률 분포 추정 metric으로 주어진 data point에 대해서, PDF의 gradient를 의미한다. 즉, 주어진 data point가 구하고자 하는 확률 분포에 대해서 얼마나 general한 값인지를 나타내난 값이다.
만약 score가 높다면, $data \sim P_{data}(x)$일 확률이 높다.
여기서 score 는 $S(x) = \nabla_x\;log\;p(x)$ 로서, 확률 밀도 함수의 gradient를 의미한다.
(과정은 참조1 , 참조2)

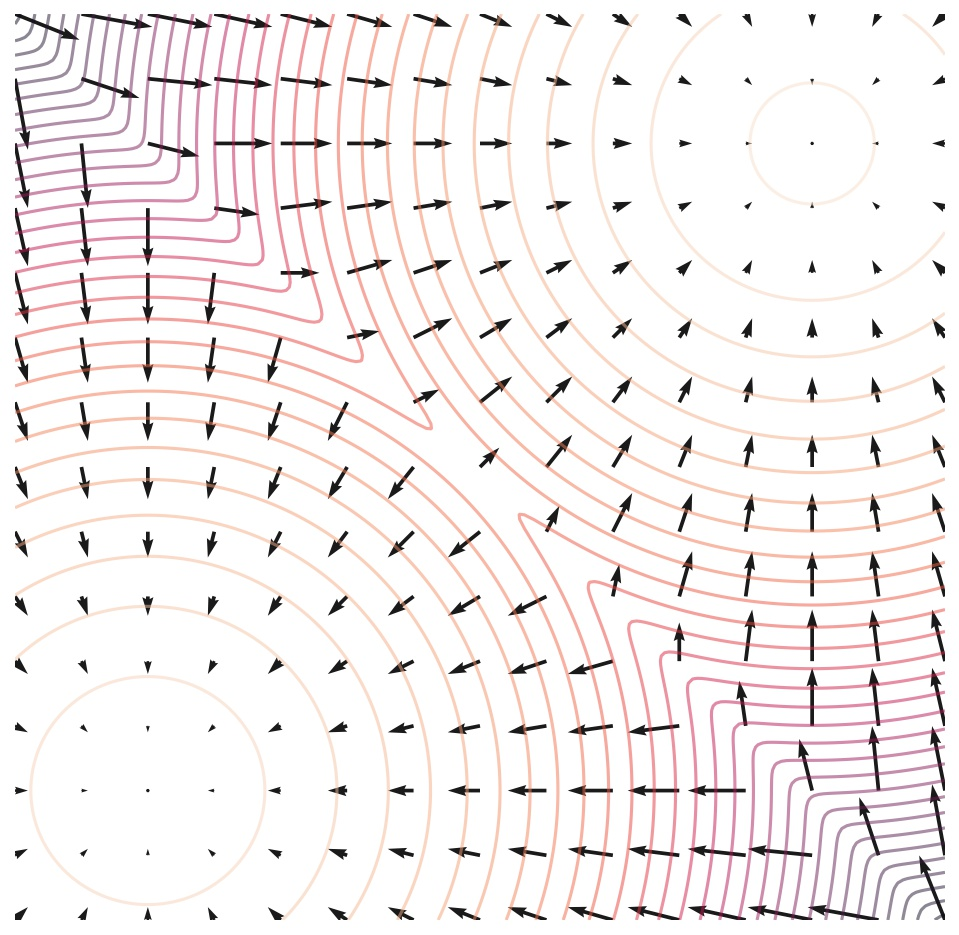
Score는 log data density가 커지는 방향에 대한 vector field로 볼 수 있는데, 밑의 그림을 보면 화살표가 score function을 의미하며, 이는 PDF가 높게 나올 장소에 대한 방향으로도 볼 수 있다.

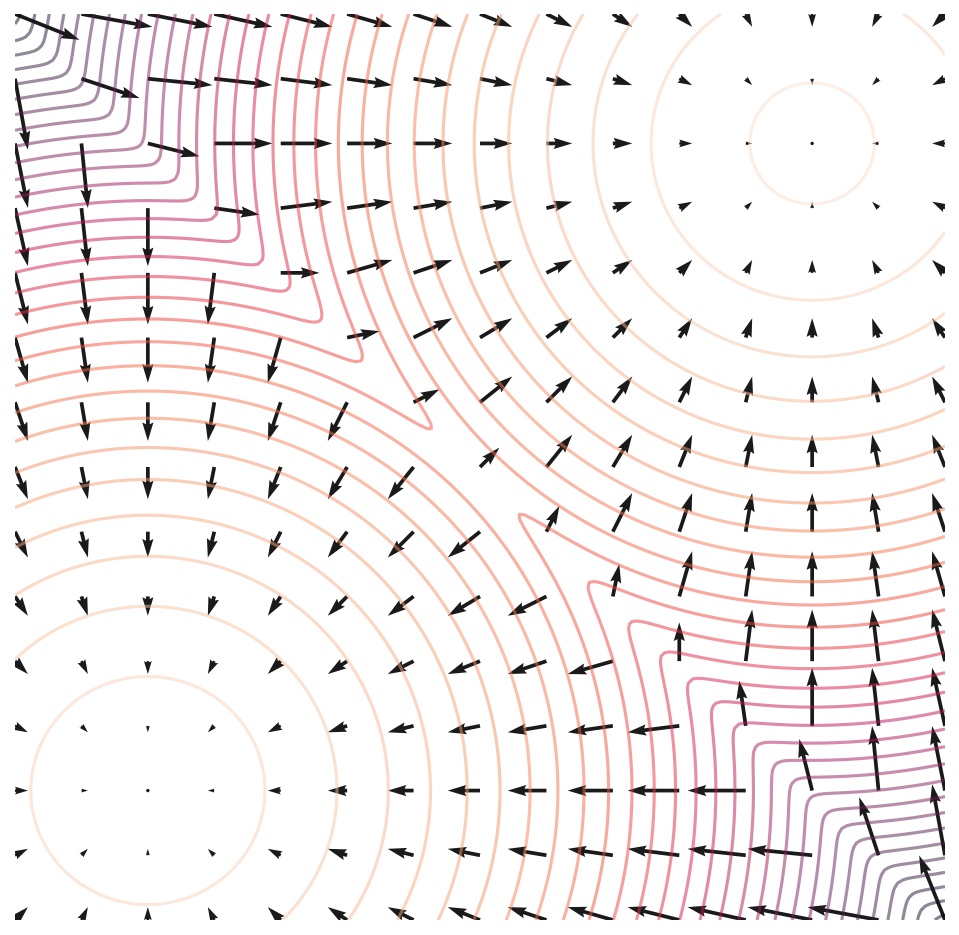
이미지 출처

---

Problem

그러나 Score function에는 2가지 중요한 문제가 있는데,
1) data distribution이 low-dimensional manifold에 놓여 있을 때, ambient space(주변 공간)의 stein은 정의되지 않을 수 있다(예를 들어 어떤 데이터가 3차원의 공간에 있다고 했을 때, 실제 데이터의 manifold는 2차원에 존재한다고 가정해보자.)
score라는 것은 PDF위에서만 계산 되는 값이므로, ($S(x) = \nabla_x\;log\;p(x)$) data의 manifold를 제외한 주변 공간에서는 score가 계산 될 수 없다는 문제점이 존재한다.

2) scarcity of training data: 데이터의 부족에 대한 문제가 존재한다.

이 2가지가 문제가 되는 궁극적인 이유는 data distribution을 transition(전이) 할때 (예를 들어 생성한 이미지에서 추가적인 특성을 가진 이미지를 생성한다고 생각해보자) low density region(score가 매우 낮거나 존재하지 않는 부분)을 통과하기 때문에 새로운 data distribution을 얻기가 어렵다는 단점이 존재한다. (vector field의 관점에서 봤을 때, low density region을 통과하면서, 어느 방향으로 가야할 지를 모르는 문제가 생긴다. (이를 모델이 low-dimensional manifold에서 "collapse"된다고 표현한다)
그림으로 보자. 밑의 True Data Score를 보면, 중간의 대각 성분에서의 Score는 존재하지 않는다. 왼쪽의 Data distribution에서 오른쪽의 Data distribution으로 이동할 때, low density region을 지나야 하는데, 이 부분에서의 Score는 구해지지 않기 때문에, Transition할 때 문제가 생길 수 있다.

---

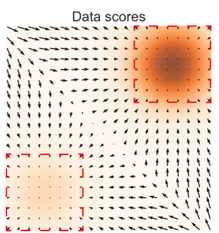
Solution

이에 대한 해결법은
1) random noise를 더해서 model이 "collapse"되는 것을 방지

• noise를 더함으로서, SGD에서의 momentum 처럼 탈출을 돕는 역활을 한다. noise가 더해지면서, 다양하게 학습을 진행하면서, 방향에 대한 확신과 변동성에 대해서 학습을 할 수 있게 된다고 한다.

2) 논문에서 사용한 Annealed version of Langevin dynamics 방법이 있다.

---

Score-based generative modeling

우선 시나리오를 제안하는데, data가 i.i.d하다는 가정으로 $\{x_i \in R^D\}_{i=1}^N$의 데이터가 $p_{data}(x)$로부터 sampling된다고 해보자. 구하고자 하는 density function을 $p(x)$로 가정하면 score는 $s_{\theta}(x) = \nabla_x\; log \; p(x)$로 정의된다.

여러 유도 과정을 거쳐서 목적 함수를 다음과 같이 정의할 수 있는데, 여기서 실제 데이터 분포에 대한 score $\nabla_x\;log \; p_{data}(x)$를 구할 수 없으므로,

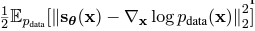
다음 식으로 유도할 수 있다.

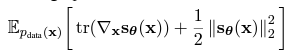
여기서 $tr(\nabla_x\; s_{\theta}(x))$는 Jacobian matrix로, 계산이 복잡하다는 단점이 있다. 이에 선행 연구는 2가지의 방법을 제시한다.

• Denoising score matching

  data point에 noise를 줘서 perturb(동요) 시키고 그 noise를 제거하는 방식으로 학습을 진행한다. $tr(\nabl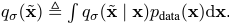a_x\; s_{\theta}(x))$를 대체하는데, 성질을 이용한다.
  (How? 이 부분을 더 찾아봐야한다. DDPM?)
  Denoising score matching을 사용했을 때의 objective function은 다음과 같다.
  
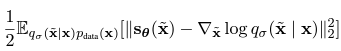
  여기서 최적의 score model $s_{\theta^*} = \nabla_x\;log \; q_\sigma(x)$가 된다.

• Sliced score matching

  Random projection을 사용하여 $tr(\nabla_x\; s_{\theta}(x))$ 를 근사한다. (마찬가지로 찾아보고 첨부)

  ---

  Random projection의 과정은 다음과 같은데,
  1: 무작위로 방향 벡터 $v$를 선택
  2: 방향으로 projection을 진행
  3: 그 point에 대해서 score를 계산
  그 때의 목적 함수는 다음과 같다.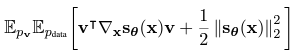

  
  여기서 $p_v$는 방향 벡터 $v$를 결정하는 간단한 distribution이라고 한다(e.g. normal distribution)

---

Sampling with Langevin dynamics

Langevin dynamics를 사용하여 sampling을 진행할 수 있다. 여기서 $z_t \sim \mathcal{N}(0,I)$이다.

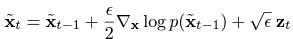
Challenges of score-based generative modeling

The manifold hypothesis

아까 위에서 data가 low-dimension-manifold에 있다면 모델이 "collapse" 될 수 있다고 하였다. 이를 논문에서는 간단한 noise를 더함으로서 "collapse" 되는 것을 피할 수 있음을 보여준다.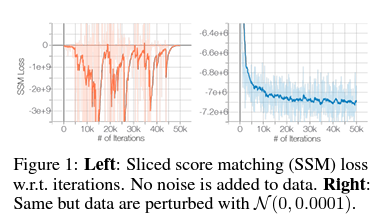
왼쪽 그림이 noise를 주지 않았을 때의 score function을 학습하는 과정이고, 오른쪽이 noise를 주었을 때의 학습 과정이다.

Inaccurate score estimation with score matching

위에서 언급한 문제중 low data density 지역에서는 score matching이 제대로 구해지지 않는다고 했었다. 밑의 그림은 이를 나타낸 것인데, GT(왼쪽)에 비해서, Estimate score(오른쪽)의 중앙을 보면, 데이터가 적은 부분의 score가 제대로 구해지지 않는 것을 볼 수 있다.

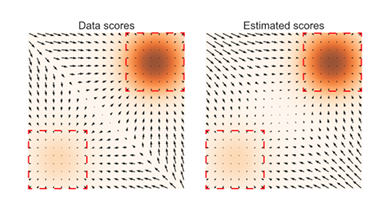
이 때의 data distribution은 다음과 같다.

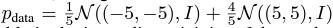
Slow mixing of Langevin dynamics

low density의 score는 또다른 문제가 있는데, 만약 data distribution이 low density regions으로 나뉘게 된다면, Langevin dynamics가 제대로 작동하지 않을 수 있다. 이를 보여주는 것이 다음 그림인데,

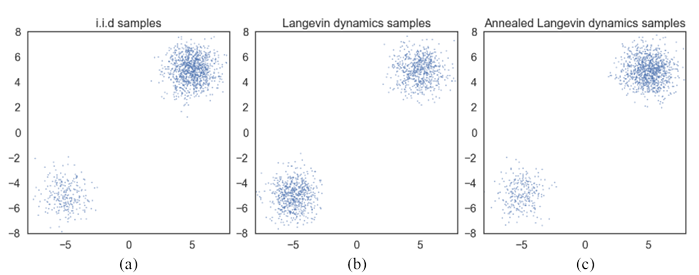
데이터의 분포가 다음과 같다고 가정해보자.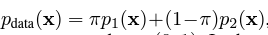
$\pi$가 data의 sampling을 결정하는 베르누이 분포라고 할 때, 실제의 i.i.d sampling의 결과는 (a)이지만, langevin dynamics를 사용할 때의 경우는 (b)처럼 균일하게 나온다고 한다. 이는 score function의 방식 때문인데, score function을 생각해보면,

$s_{\theta}(x) = \nabla_x\;log \;p(x)$인데, 우리의 실제 분포는 $p_{data}(x) = \pi p_1(x)+ (1-\pi)p_2(x)$였었다.
$p_{data}(x)$에 대해서 score function을 구해보면 우선 왼쪽 term부터
$\nabla_x log \pi \cdot p_1(x) =\nabla_x log\pi+ \nabla_x log p_1(x)$ 여기서 $\nabla_xlog\pi$는 상수이므로, $\nabla_x log \pi \cdot p_1(x) =\nabla_x log p_1(x)$이다. 마찬가지로 오른 쪽 term에 대해서도 진행을 하면

• 결국 $s_\theta(x)= \nabla_x log p_1(x)+ \nabla_x log p_2(x)$ 가 되어 버린다.

이는 실제 분포와 상관없이 균일하게 sampling이 된다는 것을 의미하며, 기존의 Langevin dynamics sampling을 사용한 multi variative distribution을 추정할 수 없다는 것을 의미한다. 이를 해결하는 것이 밑에서 나오는 NCNS방법이다.

---

Noise Conditional Score Networks: Learning and inference

NCSN

기존의 $s_{\theta}(x)$에 대해서 조건부로 noise를 주는 것인데, 여기서의 noise를 $\sigma$로 정의하여 score function을 새롭게 정의한다.
$s_{\theta}(x,\sigma)\approx \nabla_x \textrm{log}\;q_{\sigma}(x)$ where $q_{\sigma}(x) := \int p_{data}(t)\mathcal{N}(x|t,\sigma^2I)$ 기존의 데이터에 noise가 더해지는 방식.

---

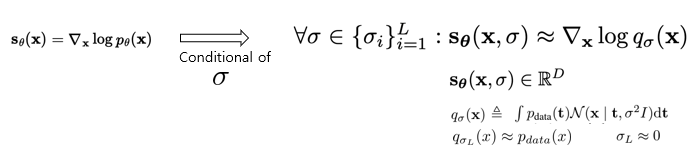
여기서 $\sigma$를 time step $t$에 따라서 각각 주게 되는데, $\{\sigma_i\}_{i=1}^L$를 positve geometric sequence로 가정하자. 이때의 $\sigma_1> \sigma_T$인데, 이는 $\sigma$가 작으면, data에 대해 거의 영향을 미치지 않고, $\sigma$가 크면 data간의 차이를 완화하기 때문이라고 한다.
즉, noise에서 sample의 차이를 완화하기 위해서 초기 $\sigma_1$는 크게 설정하고, 점차 sampling이 되는 마지막 time step $T$에서는 $\sigma_T$를 거의 0에 가깝게 하여 data에 영향을 주지 않도록 하는 것이다.

GAN 처럼 model을 noise에 대해서 NCNS를 정의하는 것이 high quality sample을 생성하는 것에 중요한 역활이 되었다고 한다.

---

Learning NCSNs vis score matching

Denoising score matching , sliced score matching 둘다 작동하지만, 계산의 속도로 인해 Denoising 방식으로 sampling을 진행한다고 한다. 우선 noise function은 다음과 같다
$q_\sigma(\tilde x| x) = \mathcal{N}(\tilde x | x, \sigma^2 I)$이 때의 score function은
$\nabla_x\;log q_\sigma(\tilde x| x) = -(\tilde x - x )/\sigma^2$ 로 정의할 수 있는데(가우시안의 미분) 아까의 denoising score matching함수
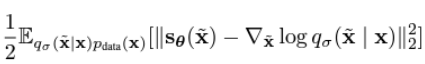에 $\nabla_x\;log q_\sigma(\tilde x| x) = -(\tilde x - x )/\sigma^2$를 집어 넣으면, 목적함수는 다음과 같이 구해진다.

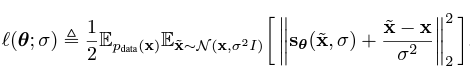
• $\tilde x \sim \mathcal{N(x,\sigma^2I)}$임을 확인하자.

여기서 NCSN을 사용할 것이기에, sigma를 time step에 대해서 정의하기 위해 최종적인 수식은 다음과 같이 정의가 된다.

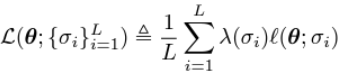
위의 수식이 성립하기 위해선 최적의 score function $s_{\theta^*}(x,\sigma_i) = \nabla_x\;log\;q_{\sigma_i}(x)$일 때만 성립한다.(if and only if)

이때 $\lambda(\cdot)$에 대해서 많은 선택이 있을 수 있지만, 우리는 언제나 그렇듯, 계산의 편의성을 위해 $\lambda(\sigma_i)\ell(\theta;\sigma_i)$가 모든 $i$에 대해서 동일했으면 한다. 논문의 저자들은 경험적으로 $||s_{\theta}(x,\sigma)\propto \frac{1}{\sigma}||_2^2$를 얻어 냈다고 한다. 따라서
$\lambda(\sigma) = \sigma^2$로 설정했다고 한다.

위의 trick을 사용하여 최종적인 수식은

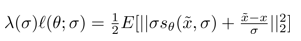
$\lambda(\sigma)\ell(\theta;\sigma)= \frac{1}{2}E[||\sigma s_{\theta}(\tilde x,\sigma) + \frac{\tilde x - x}{\sigma}||_2^2]$가 되고, 여기서 $\frac{\tilde x - x}{\sigma} \sim \mathcal{N}(0,I)$이고($q_\sigma(\tilde x| x) = \mathcal{N}(\tilde x | x, \sigma^2 I)$로 설정하였기 때문), $||\sigma s_{\theta}(x,\sigma)\propto 1||_2$이기에 $\sigma$에 not dependent 하다고 한다.

최종적인 알고리즘은 다음과 같다.

---

Comment

NCSN 에서 $\sigma$를 변화시키며 넣어 주는 이유는 결국, 기존의 Langevin dynamics로는 low density 부분을 accurate 할 수 없기에, data의 density를 분산($\sigma$를 키워서) low data density에도 data가 존재하게끔 하는 것.

• low data density가 있을 때의 score function의 경우

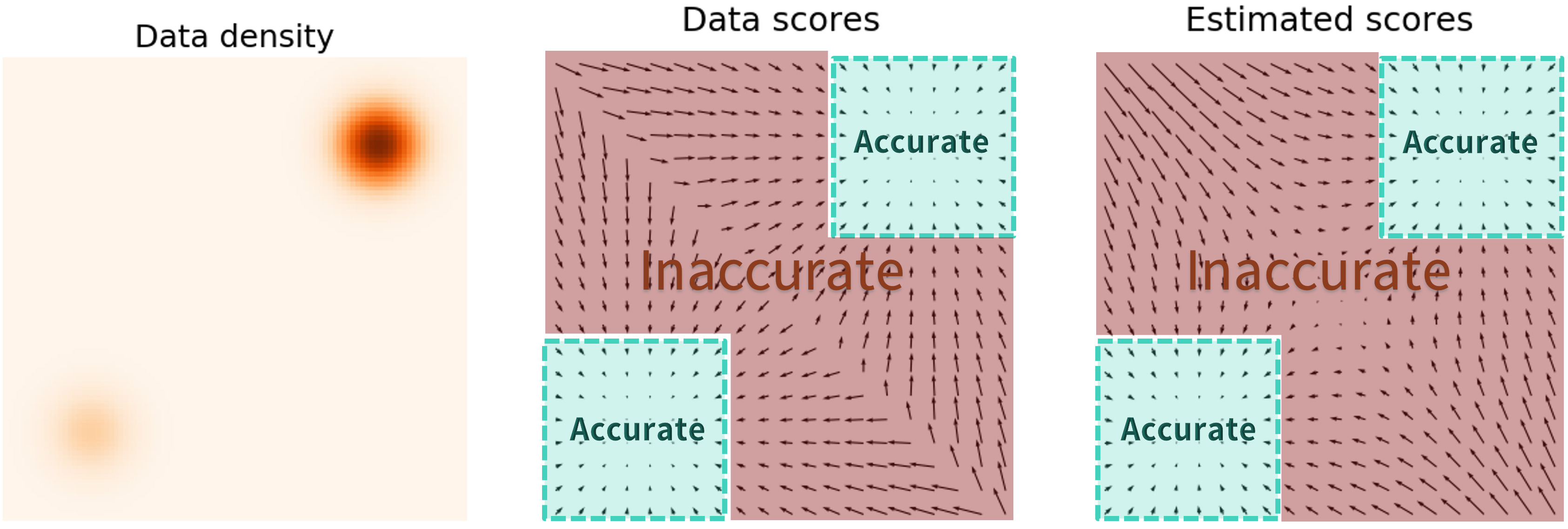
• sigma를 키웠을 때의 score function의 경우

그러나 $\sigma$가 크면 data의 정확한 density를 추정할 수 없으므로, sigma를 계속해서 바꿔 주는 것.
$\sigma$를 계속해서 바꿔주는 이 방법을 annelad Langivin dynamics라고 하는 것이고,
score function에 $\sigma$를 조건부로 넣어주는 모델을 NCSN이라고 정의한다.

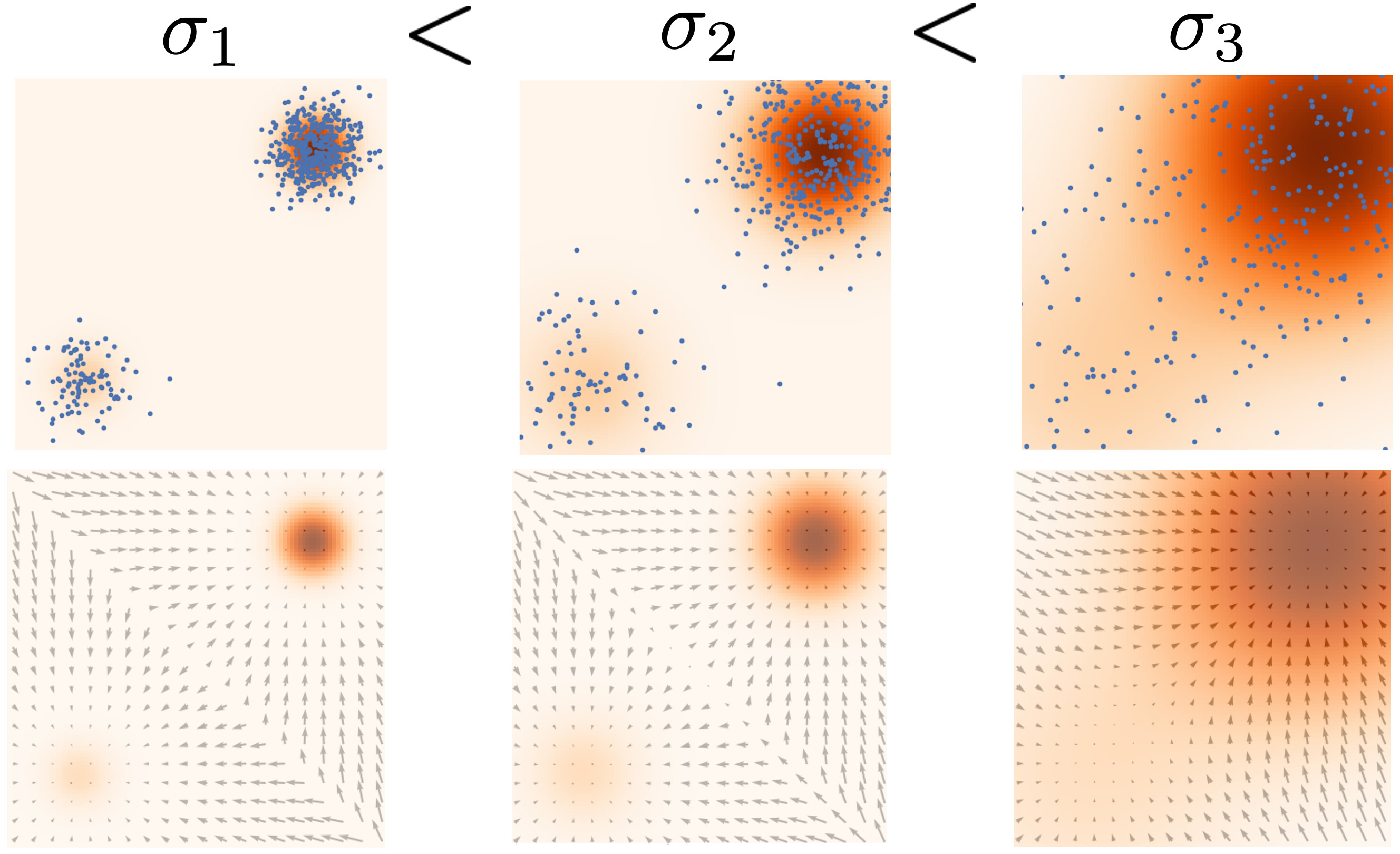
위 그림에서는 1-> 3순으로 sigma가 커지는 것을 보여주는데, 그림에서 보이듯,
$\sigma$가 작으면, low density를 잘 맞추지만, score function이 존재하지 않는 부분이 생기고, sigma가 클 수록 모든 부분에 대해서 score function이 구해지는 것을 볼 수 있다.

이를 통해 NCSN model은 $\sigma_{large}$를 $\rightarrow$ $\sigma_{small}$ 로 바꾸면서 sampling의 결과를 더 좋게 만드는 결과를 보여줄 수 있다.

Appendix

---

• $\nabla_x\;log q_\sigma(\tilde x| x) = -(\tilde x - x )/\sigma^2$ 에 대해서 직관적인 해석이 부족하여 추가적인 설명을 하려고 한다.

우선 가우시안 분포에 대해서 생각을 해보자.
가우시안은 $p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$으로 정의가 될 때, 평균에 대한 가우시안의 score function은 $\nabla_xlog p(x)$이다.
위에서 정의한 가우시안에 log를 씌운후, $\mu$에 대해서 편미분을 구하면 앞의 분모는 사라지게 될 것이고, exp는 log를 씌워서 사라진다. 따라서, $\frac{\partial \ln p(x)}{\partial \mu} = \frac{x - \mu}{\sigma^2}$로 구할 수 있다.

여기서 조건부 가우시안을 가정해보자. $p(\tilde x|x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(\tilde x-x)^2}{2\sigma^2}\right)$ 조건부에 대해서 가우시안을 정의하면 평균이 조건부인 $x$가 되어버린다. 이때 가우시안의 평균이 $x$가 되는 이유는 분포가 주어진 조건부 $x$를 중심으로 샘플링이 되기 때문이다.

정리하면, $x$가 주어졌을 때, $\tilde x$는 $x$를 중심으로 가우시안 분포를 가지게 되고, 이에
우리는 $p(\tilde x | x) = N(\tilde x|x,\sigma)$로 정의할 수 있다.

• 다변량 가우시안 분포의 경우는 다음과 같다.

$p(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^D|\Sigma|}} \exp\left(-\frac{1}{2}(\mathbf{x}-\mu)^\top\Sigma^{-1}(\mathbf{x}-\mu)\right)$

$Q(\tilde{x}|x) = \frac{1}{\sqrt{(2\pi)^D|\Sigma|}} \exp\left(-\frac{1}{2}(\tilde{x}-x)^\top\Sigma^{-1}(\tilde{x}-x)\right)$
where $|\Sigma|$ is determinant

---

Appendix 2

저자들의 github를 가보면, 가우시안의 MLE에 대해서 다음과 같이 정의가 되어있다.

  def log_prob(self, samples, sigma=1):
        logps = []
        for i in range(len(self.mix_probs)):
            logps.append((-((samples - self.means[i]) ** 2).sum(dim=-1) / (2 * sigma ** 2) - 0.5 * np.log(
                2 * np.pi * sigma ** 2)) + self.mix_probs[i].log())
        logp = torch.logsumexp(torch.stack(logps, dim=0), dim=0)
        return logp

여기서 mixprob는 self.mix_probs = torch.tensor([0.8, 0.2]) 분포의 비율이다. 이를
수식으로 정리를 해보면, $r_j$, $j$ 번째 mix probs이라고 할 때,

$\sum^n_{i=1} \frac{-(x_i-\bar{x})^2}{2\sigma^2} - 0.5log \ 2 \pi \sigma^2 +log r_j$

$= log r_j \ \frac{1}{\sqrt{2 \pi \sigma^2}} e^{\sum^n_{i=1} \frac{-(x_i-\bar{x}_j)^2}{2\sigma^2}}$

$= log \prod ^n_{i=1} r_j \ \frac{1}{\sqrt{2 \pi \sigma^2}} e^{\frac{-(x_i-\bar{x}_j)^2}{2\sigma^2}}$

$= log \prod ^n_{i=1} r_j \ N(x_i| \bar{x}_j, \sigma^2I)$

$= \sum^n_{i=1} log \ r_j N(x_i| \bar{x}_j, \sigma^2I)$

로 유도가 되는 것을 알 수 있다. 결국 $\nabla_xp(x)$에서 $p(x)$를 가우시안으로 가정한 것과 같으며,
첫 번째 식을 생각해보면
$\sum^n_{i=1} \frac{-(x_i-\bar{x})^2}{2\sigma^2} - 0.5log \ 2 \pi \sigma^2 +log r_j$

where

• $\frac{-(x_i-\bar{x})^2}{2\sigma^2}$는 $p(x)$의 score,
• $0.5log \ 2 \pi \sigma^2$는 sigma에 대한 term
• $log r_j$: 비율에 대한 log 값. (Constant)로 분해가 되는 것을 볼 수 있다.
  여기서 중요한게 $0.5log \ 2 \pi \sigma^2$가 만약 Annealed 를 사용하지 않는 다면(sigma를 변수로 보지 않는 다면) 상수가 된다는 점이다.
  이로서, Annealed가 사용하면 sigma에 대한 term도 함수로 볼 수 있다는 것을 알 수 있다.