논문 저자들의 구현 링크
실험

Summary

MeshSegNet을 사용하여 3D dental surface model의 multi-Scale Mesh data를 segmentation을 진행한다.

Points

• multi-scale graph-constrained learming module(GLM)을 제안하는데 이는 CNN을 모방하는 연산을 한다고 한다. 이를 MeshSegNet의 forward에 통합하여 사용한다.

• local-to-global feature(cell-wise feature,multi scale contextual features , translation-invariant holistic feature)를 결합하기 위해서 dense skip-connection을 사용한다.

• end-to-end가 끝나고 graph-cut을 이용하여 isolated false prediction과 non-smooth boundaries를 refinement(세련)하게 만든다. (labeling result를 개선)

graph cut background

graph cut은 그래프 이론과 컷 이론을 기반으로 하는 영상 처리 기술이다.
$\mathcal{V}$: graph
$\mathcal{A}$: subset of nodes
$\mathcal{\bar{A}}$: complement of set $\mathcal{A}$
일때, $\mathcal{A}\subset \mathcal{V}$로 표시할 수 있고, $\mathcal{A} \cup \mathcal{\bar{A}}=\mathcal{V}$ 이다.
그래프 $\mathcal{V}$를 $K$개의 중복없는 subset($\mathcal{A}_1,\mathcal{A}_2,\cdots,\mathcal{A}_k$)로 분할한다고 하면 다음과 같이 정의할수 있다.
$cut(\mathcal{A}_1,\mathcal{A}_2,\cdots,\mathcal{A}_k) = \frac{1}{2}\sum_{k=1}^K|(u,v)\in \mathcal{E} : u\in \mathcal{A}_k,v\in \mathcal{\bar{A}_k}|$

introduction

치과에서 임상 실무를 위해 3D 치아 표면 모델을 정기적으로 모델링을 진행하는데, 이는 환자들에게 불편한 경험이 될 수 있다. 이에 IOS(Intraoral scanner)라는 장비가 직접 치아의 디지털 표면 모델을 재구성한다. 그러나 3D치과 표면에 정확한 치아 label을 부여하는 것은 매우 어려운 task인데, 이에 관한 Automated method를 고안하는 것은 여러 문제가 존재한다.
1) 치아의 형태는 환자와 위치에 따라 극명하게 다르다
2) 환자의 치아는 일반적으로 정렬 오류와 혼잡으로 인해 비정상적인 외관을 갖는다.

3D IOSs의 활용은 치아 라벨링을 어렵게 만들며, 원시 표면의 비-치아 부분 (예: 잇몸 조직)은 일반적으로 불규칙한 모양을 갖고 있기에, 구강 내 깊은 영역 (예: 제2/제3대 사람 이)은 광학 스캐너에 완전히 포착되지 않을 수있다고 한다. 3D model을 pointcloud의 관점으로 automated method를 해결을 하려고한 선행연구들(pointnet, pointnet++,PointConv)들이 존재한다. 그러나 pointcloud는 single point만을 고려한다. (x,y,z의 좌표만을 가지고 있음) 이를 극복하기 위해 Mesh데이터를 input으로 하는 MeshNet이라는 개념이 나왔다. Mesh데이터는 cordinate의 정보와 faces(인접한 n개의 vertex)의 정보를 가지고 있는 사용하기에 pointcloud보다 정보량이 더 많다는 장점을 가진다.

본 논문에서는 MeshNet과 mesh의 Adjcency정보를 사용하여 GLM이라는 모듈을 설계하고, 또한 graph-cut algorithm을 사용하여 더 세밀한 정보를 얻는다. 이를 바탕으로 teeth segmentation을 진행한다.

purpose

기존의 pointcloud를 사용한
본 논문은 raw dental surfaces의 high-level geometric feature를 학습하는 것을 목표로한다. 또한 PointNet의 확장인 MeshSegNet이라 불리는 end-to-end deep-learning method를 제안한다.
본 논문에서 주장하는 4개의 큰 흐름이 있다.

1) 단일 점의 좌표(x,y,z)만 사용하는 대신, 인접한 셀들을 공유하는 공통 vertex로 자연스럽게 연결되는 세 개의 셀 꼭지점의 좌표를 주요 네트워크 입력으로 채택한다. 이를 통해 mesh 셀들의 공간 의존성을 암묵적으로 고려한다고 한다. 또한, 전체 표면에 대한 셀의 법선 벡터와 상대 위치도 추가적인 입력으로 포함하여 더 포괄적인 셀 설명을 위해 사용.(여기까지는 MeshNet의 개념이다.)

2) multi-scale graph-constrained learning modules을 제안하고, MeshSegNet의 forward 경로에 이를 통합하여 표면 상에서 CNN이 계층적으로 모델링하는 것을 흉내낸다.

3) dense fusion strategy를 설계하였는데, 이는 밀집한 스킵 연결을 채택하여 로컬에서 전역까지의 특징 (즉, 셀별 특징, 다중 스케일 문맥적 특징 및 변환 불변 전체적 특징)을 결합한다고 한다. 이를 기반으로 더 높은 수준의 특징을 추출하여 mesh cell의 annotation을 진행(labeling을 annotation(주석)이라고 표현하는 듯 하다)

4) MeshSegNet에 의한 end-to-end 예측 후에는 그래프 컷 과 치과 표면의 기본 기하학적 특성 을 기반으로 효율적인 postprocessing을 적용하여 치아 라벨링 결과를 더욱 정교하게 개선

Data and pre-processing

Dataset: 3D 치아 스캐너 data, 각 표면은 100,000개의 mesh cell/triangels를 가지고 있다.

preprocessing: 원래의 토폴로지가 보존되도록 10,000개의 셀로 다운샘플링을 진행 class C=14 치아가 존재하고, 양쪽의 오른쪽과 왼쪽에 UR1-UR7 및 UL1-UL7로 표시. 각 cell의 표면은 15-D개의 input-vector로 구성되어 있으며, 셀 정점의 좌표 (9개 요소)를 주요 입력으로 사용하며, 각 Mesh 셀의 법선 벡터 (3개 요소)와 전체 표면에 대한 각 셀의 상대 위치 (faces)를 보조 label로 사용(MeshNet내용)

Model

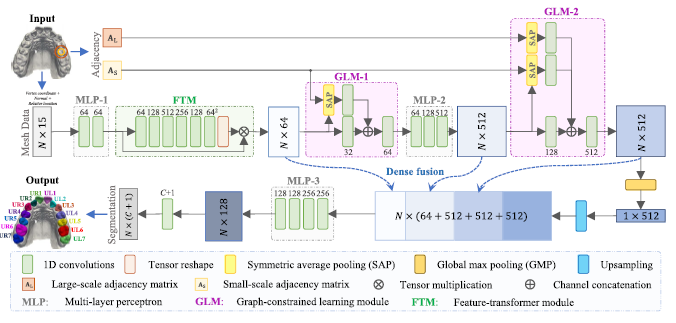
input raw surface : $F^0 \in \mathbb{R}^{N \times 15}$ where $N$: number of Mesh cell 여기서 주의 깊게 봐야할 것은 input이 mesh cell이다. (point num이 아님)
output : $N\times(C+1)$ : 1은 아마 잇몸(gingiva)를 의미한다.

model의 초반부를 보면 input으로 $F^0$를 입력으로 받는데, 이를 MLP_1을 통과한다. 이때의 output을 $F^1$이라고 하자. MLP_1는 논문에서 mesh cell의 high-level geometric features를 추출하는 역활을 한다고 한다.

$F^1$는 2가지로 forward되는데 하나는 FTM(feature transformer module)을 통과하고 하나는 FTM의 output과 Matrix product 연산을 수행한다. 즉 FTM output $T\in R^{64\times 64}$
$\hat F^1 = F^1T , F^1\in \mathbb{R}^{N \times 64}$이다. FTM은 pointnet의 T-net처럼 feature의 transform을 학습하는 small network이다.

$\hat F^1$은 GLM(graph-constrained learning modeuls)의 input으로 들어가는데 GLM은 각 셀을 중심으로 삼아 다른 반지름을 가지는 2개의 3D 구를 가정한다.($A_s,A_L$는 각각 $r_s,r_L$의 반지름을 사용해서 생성함. ) 이를 기반으로 입력 메시 데이터에 대해 2개의 NxN adjacency matrix를 구성한다.
논문에서는 Adj matrix를 생성하는 구의 만지름을 각각 $r_s=0.1, r_l=0.2$로 설정하였다.

Adj matrix를 기반으로 GLM_1은 SAP(Symmetric average pooling)을 사용하여 graph-based fusion operation을 진행한다. 이를 수식화 하면 다음과 같은데
$\tilde{F^1}= fsap(\hat{F^1}|A_s)= \tilde{D}_S^{-\frac{1}{2}}\tilde{A}_S\tilde{D}_S^{-\frac{1}{2}}$ 여기서 $\tilde{D}_S^{-\frac{1}{2}}$는 diagonal degree matrix이고, $\tilde{A}_S= A_s+I$이다.

즉, GLM의 SAP연산은 Graph-convolution 연산을 의미한다. 조금 더 자세하게 살펴보면 ,GLM_1의 output을 $F^{S1}$라고 했을 때, $F^{S1}=\sigma(\{\sigma(\hat{F^1}W^1)\oplus\sigma(\hat{F^1}W^1)\}W^2)$ 로 나타낼 수 있다.
여기서 왼쪽 Term $\sigma(\hat{F^1}W^1)$는 FTM을 통과한 output이고,
$\sigma(\tilde{F^1}W^1)\} = \sigma(\tilde{D}_S^{-\frac{1}{2}}\tilde{A}_S\tilde{D}_S^{-\frac{1}{2}}\hat{F^1}W^1)$는 sap연산을 적용한 결과이다.

여기서 재미있는 것은 GLM_2에선 $A_s,A_L$ 2개의 Adj matrix를 사용한다는 것이다. 즉, 2개의 병렬 sap연산을 수행하고, 위의 GLM_1처럼 $\oplus$(element wise plus)연산을 적용하여 activation function을 통과한다. 그 외에의 나머지는 그림에서 직관적으로 확인할 수 있듯이 pointnet처럼 local, global feature matrix를 사용하여 segmentation을 진행한다.(그래서 MeshSegNet이 pointnet의 확장이라고 설명한 듯 하다)

graph-cut

논문의 output result를 post processing을 진행하는데, graph cut이라는 알고리즘을 사용한다. 즉, final label map $L = \{L_i\}_{i=1}^N$ with $L_i\in\{1,...,C+1\}$는 graph cut에 의해 결정되는데 이는 다음과 같다

$\operatorname*{argmin}_L\sum_{i=1}^N-\operatorname*{log}(P_{i,L_i}+\epsilon)+\lambda\sum_{i=1}^N\sum_{i^*\in \mathcal{N_i}}\mathcal{C}(L_i,L_{i^*})$
각각을 살펴보면 $\epsilon$은 아주 작은값 (1e-4)이고 ,

$\mathcal{C}(L_i,L_{i^*})= (1-\delta(L_i,L_{i^*}))\times \psi(s_i,s_{i*})$
이다. 이때
$\delta(L_i,L_{i^*})$: Dirac delta function 로서, 전체 영역의 면적이 1이라는 특징이 있다. 이때,다음이 성립한다.
($1 \;\operatorname*{iff}\; L_i=L_{i^*}$)

$\psi(s_i,s_{i*})={\gamma}_{i,i^*} \times \text{log}(\frac{\theta_{i,i^*}}{\pi})\times d_{i,i^*}$
$\theta_{i,i^*}$는 이웃한 주변의 cell $s_i, s_{i^*}$사이의 각도이고,
${\gamma}_{i,i^*}$는 $\theta_{i,i^*}$가 concate 하면 1 아니면 $|n_i,n_{i^*}|$이다.
$d_{i,i^*}$는 cell $s_i$와 그것의 이웃 cell $s_{i^*}$의 거리를 의미한다. (논문에서는 Euclidean distance로 나타내고 있다.)

Metric

loss function은 segmentation에서 일반적인 Dice score loss를 사용하였으며, 다른 모델과의 평과 지표로서는 3가지로
1) Dice similarity coefficien(DSC),
2) Sensitivity (SEN),
3) positive prediction value(PPV)를 사용하였다.

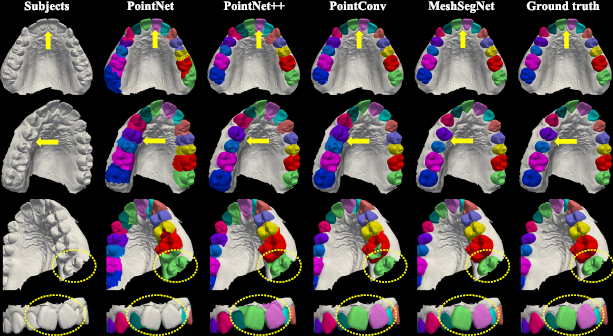
pointnet, pointnet++,pointconv에서 잘 분별하지 못하는 노란 원을 MeshSegNet에선 잘 검증하고 있다.

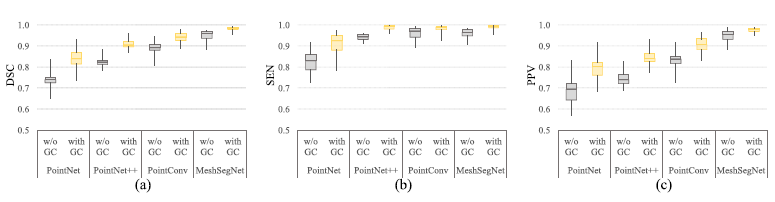
다양한 model과 비교하였을 때 MeshSegNet이 더 낫다는 것을 논문에서 보여주고 있다.
특히, post processing으로 graph-cut을 사용한 것이 모든 모델의 일반적인 성능을 향상시키고 있음을 입증하였다.