Batch에 대하여

Dataset에 대해서 batch를 나누었다고 할 때, 한 epoch에 대한 업데이트는 batch별로 이루어 지는가? 아니면 그냥 이어서 진행이 되는가?

질문이 들었던 이유: batch를 나누는 이유가 뭘까? 가 궁금했었다.
https://cafe.naver.com/bakingschool/309807- 우선 batch를 나누는 확실한 이유는 dataset의 용량이 너무 커서, memory에 올릴 수 없기 때문에, dataset을 쪼개서 memory에 올리기 위함이다.
그리고 드는 생각은, 만약 batch별로 학습이 진행이 된다고 하면, 그건 초기값을 여러번 설정해서, 최적의 global optimization value를 찾는데 도움이 되지 않을까? 하는 의문이 들었었다.

답

우선 답을 먼저 말하면, 아니었다. 한 batch에 대해서 학습이 끝나면, 학습된 weight를 가지고 다음 batch에 대해 학습을 진행하고, 모든 batch에 대해서 학습이 끝난다면, 그것이 한 epoch이 끝난 것이고, epoch을 계속해서 진행하면서, 최적의 weight를 구하는 것이다. 그러면 SGD란 무엇인가?

SGD와 batch의 의미

우선 loss function $J(\theta) = \frac{1}{m}\sum_{i=1}^m|\hat{y}-y|^2$이라고 가정하자 그러면 이 function은 다음과 같은 그래프를 그리게 된다.

이때 , 그렇다면 자연스레 들어야 하는 생각은 과연 batch를 나누어서 gradient decent algorighm를 이용하여 parameter를 구하는 것과 $J(\theta)$를 gradient decent algorighm을 통해서 구한 값과 같을까? 이에 대한 정답은 아니다. (물론 대부분은 확신 할 수 없다. 라는 표현이 정확하다.)
왜냐하면 우리가 구하고 싶은 weight는 $\nabla J(\theta)$했을 때 0에 가까운 값이지, $\nabla J^{B}(\theta)$ {B는 batch를 의미} 를 구하고 싶은 것이 아니기 때문이다.

• 즉 batch를 나눠서 진행하는 SGD는 $J(\theta)$를 미분하는 GD와는 다른 것이다.
• 그러나 결과적으로 말하면, SGD는 $J(\theta)$를 $J$의 최소점을 잘 찾는다.

$J(\theta)^{\{B\}}$ $\not =$ $J(\theta)$임에도 불구하고 어떻게 잘 작용을 하게 되는 것일까?

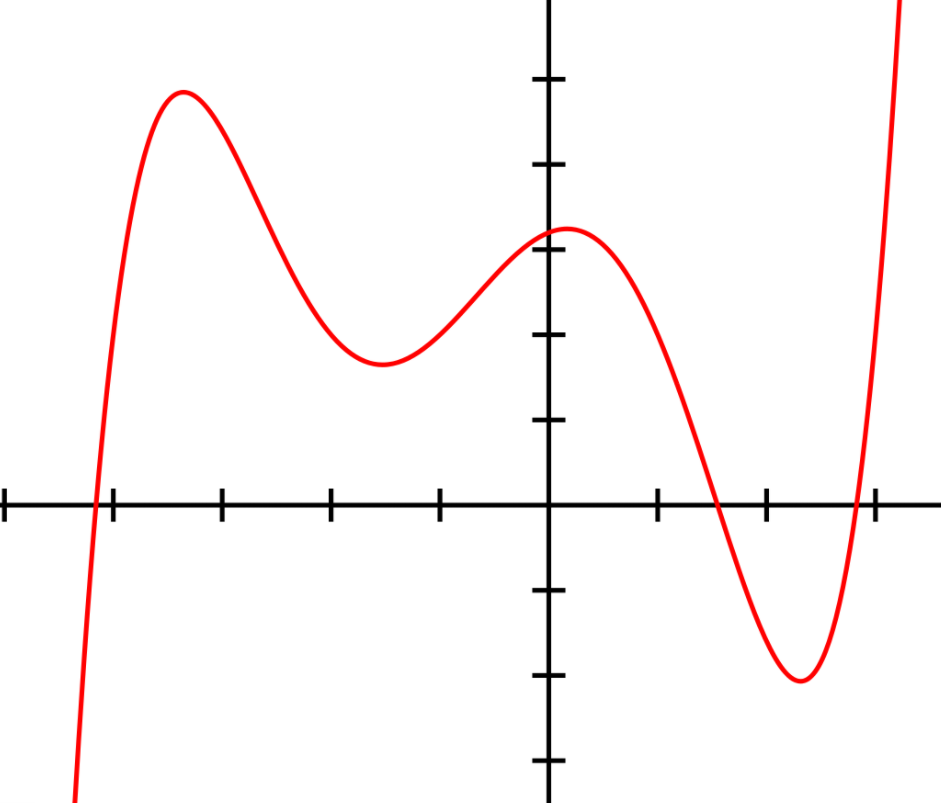
SGD는 기하학적인 의미로, saddle point를 극복하는 것에서 의의를 둔다. 예를 들어,
cost function이 이런 식으로 생긴 5차 함수라고 가정해보자. 그래프의 눈금을 1이라고 뒀을 때,
초기값이 -3에서 시작하면, -2<x<-1 에서 gradient값이 0이 되게 되는 saddle point에 빠지게 된다.
saddle point에서는 gradient값이 0이 되므로, lr을 아무리 줘도 weight가 학습이 되지 않는다.

이를 이해하기 위해선 convex라는 개념에 대해서 이해해야한다. 우선 convex란 단어의미 그대로, 볼록하게 생긴 형태를 convex라고 한다. $\alpha f(\theta_0) + (1-\alpha)f(\theta_1)> f(\alpha\theta_0+ (1-\alpha)\theta_1)$을 만족하는 모든 식을 convex라고 한다.
이 식에서 x1= -2, x2 = 4라고 했을 때, 두 선을 나타내는 식은 $\alpha f(x_0) + (1-\alpha)f(x_1)$이다. 즉, a의 모든 확률을 표현한 식은 두 점을 잇는 식이 된다. 이때, $\alpha f(x_0) + (1-\alpha)f(x_1)$이 $f(\alpha\theta_0+ (1-\alpha)\theta_1)$보다 크다면, 그것을 convex한 상태라고 한다.

요약,

• 한 epoch이 끝났다고 하는 것은, 각 batch에 대해서 순서대로 weight를 학습하고, 모든 batch가 끝나면 한 epoch이 끝났다고 정의한다.

---

• SGD는 생각보다 동작하는 것이 어려운 알고리즘이다.

---

• batch로 나누는 순간 데이터의 분포가 기존과는 달라지기 때문에, 전체 Batch에 대한 SGD값과 Minibatch SGD의 값은 다를 수 밖에 없다.

---

• 데이터의 분포가 달라지는 문제임에도 불구하고 잘 동작하기 때문에 우리는 SGD를 사용한다.

convex는 최적화 이론에서 나오는 개념으로, 아직 부족 한 것이 많은 상태라 좀 더 공부를 해보면서 수정해야 할 것 같다.