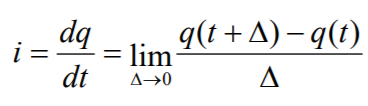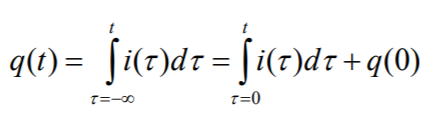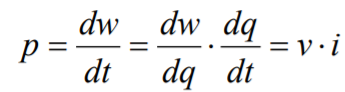Electric Circuits and Current

학교에서 수업을 들으면서 정리를 해보려고 한다.
주의 해야할 점은 용어를 정확하게 매칭시키는 것. 비슷한 용어가 많고, 단어의 뜻은 알아도, 표기법이 헷갈릴 수 있으니, 표기와 의미를 정확하게 이해하고 넘어가자.
본 내용에 나오는 사진은James A. Svoboda, Richard C. Dorf의 "Introduction to Electric Circuits 9th" 에 나오는 사진을 인용하였습니다.

전기의 장점:

mobility & flexibility.
에너지 전송이 비교적 쉽다. 다른 형태로의 에너지 변환 용이.

전기 회로(Electrical element)

전류가 지속적으로 흐를 수 있도록 전기소자가 폐쇄회로로 상호 연결된 것.

폐쇄회로란? (closed circuit)
사진출처

폐쇄회로: 사진에서 보이듯, 전류가 흐를 수 있도록 끊어짐이 없는 상태
열린 회로: 오른쪽 사진을 보면 회로의 왼쪽 상단이 끊어져 있어서, 전류가 흐르지 않는 것을 볼 수 있다.

회로소자

단자(terminal)

전기 회로나 전자기기 등에서 전류의 압력이나 출력부분에 전극을 접속시키기 위해 붙이는 끝부분. 위키
회로의 최소 단위는 2단자이다.

전하(Charge)

전기량. 보통 q로 표시, 단위는 [C] , (Coulomb, 쿨롬이라고 발음)
전선을 흐르는 전하는 보통 전자들의 집합을 의미한다.
(ex: 전선을 절단해서 쏟아지는 전자를 다 모으면 그것이 전하이다.)

1C는 매우 큰 단위이며, 약 $6.25 * 10^{18}$개의 전자나 양성자들의 전하량이다.
https://ko.wikipedia.org/wiki/%EC%A0%84%ED%95%98

전류(Current)

회로의 한 점에서 흐르는 전하의 시변화율.
시변화율: 전기줄의 한 지점을 통과할 때, 그것을 기준으로 변화율이라고 한다.
보통 i로 나타내고, 단위는 [A],(Ampere) 로 표기
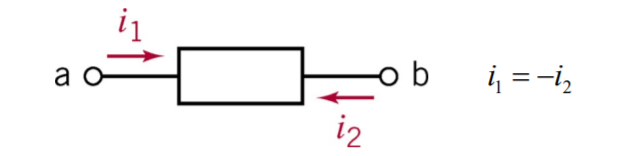
주의! 전류를 표시할 때, 방향에 따라 부호가 변한다.
$i_1$이 a에서 b로 가는 것을 +라고 했을 때, b에서 a로의 전류 $i_2$는 $-i_1$으로 표현이 가능하다.

Charge & Current의 연관성

전하와 전류는 서로 연관된다.

전류 $i$는 전하를 시간으로 미분한 값으로 표현이 가능하다.

• 전류가 전선을 지나가고 있다고 할 때, 특정 부분을 정해서 시간에 대해 미분을 하면 전류를 구할 수 있다. 그 식은 다음과 같다.

  
• 쉽게 이해하면) 전선을 한 단면으로 잘라서 그릇에 담는다고 할 때, t의 시간동안 쌓인 값을 미분한 값.

전류가 전하를 미분한 값이므로, 뒤집어서 생각해보면, 전하란 전류를 적분한 값이다. 그 식은 다음과 같다.

내가 이해한 예시) 위의 예시에서 그릇에 쌓인 전류를 다 모으면 전하이다.

직류(DC , Direct Current)

크기가 일정(stationaly하게)한 전류
왼쪽을 보면, 시간이 지나도 ,V는 일정한 것을 알 수 있다.

전압(Voltage)

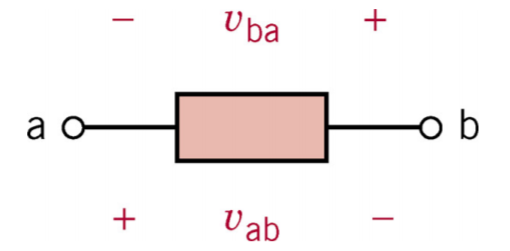
• $V_{ab}$ terminal b에 대한 terminal a의 전압
  전하를 이동시키려는 원동력이며, 단위전하를 -에서 +단자로 이동하는데 요구되는 에너지이다.
  (전류의 방향이 +에서 -로 이동하는데, 이를 -에서 +로 즉 반대로 움직이는 만큼의 힘(물리력)의 크기를 전압이라고 한다.)
• 전압은 상대적인 값을 나태낸다. 전류란 전하가 얼마나 빨리 지나것인지 를 확인하는 것이라면, 전압은 단자 B에 대한 단자 A의 전압으로서 단자 사이에 비교되는 물리량을 의미한다.
• terminal a, b가 있다고 했을 때, a<b이면 + b>a라면 -로 표시한다. 즉 $v_{ab} = -v_{ba}(a<b)$
  
• 또한,$v = \frac{dw}{dq}$ 즉 에너지(watt,전력)를 전하로 미분한 값과 같다.
• 1C 의 전하가 1V의 전위차를 이동하는데 드는 에너지를 1J(줄) 이라고 부른다.(J은 Nxm 즉 힘x거리이다.)

전력(Watt) and 에너지(Joule)

$p$: 전력[$W$(Watt)]: 생산되거나 흡수되는 에너지의 시변화율(시변화율: 시간에 대한 미분값)

• 전압과 전류의 합성 함수의 미분법을 사용해 구할 수 있는데, 결국 전력 $p$는 $v*i$, 전압X 전류 로 표현할 수 있다.
  주의! 전압과 전류는 해당 소자의 전압과 전류이다. 타 소자는 포함하지 않는다.
  ($v = \frac{dw}{dq}$: 에너지를 전하로 미분, $i = \frac{dq}{dt}$: 전하를 시간으로 미분 )

---

$w$:에너지[$J$(Joule)]

• 위의 식에서 $p = \frac{dw}{dt}$이므로, 에너지 $w = \int_{-\infty}^{t} p(\tau) \,d\tau$가 성립한다.
  즉 처음부터 t시간까지의 전력을 적분한 값이 에너지의 총 량이 된다.

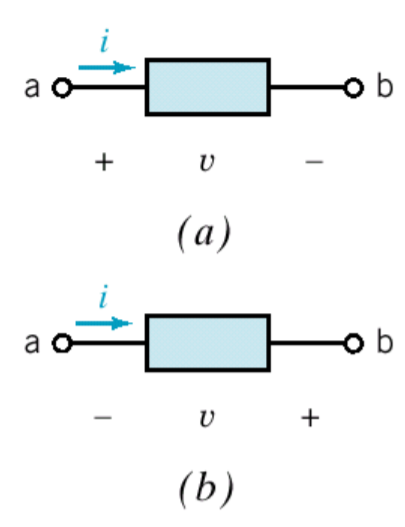
소자 표기법(Passive convention)

(a)를 전력 흡수(소비)라고 부르고,
(b)를 전력 공급(생산)이라고 한다.

• (a)의 경우, 전류i가 +방향으로 흐르는 것을 확인 가능하며, (b)의 경우 전류 i가 -방향으로 들어가는 것을 확인가능한데, (a)의 예시로는 꼬마전구, (b)의 예시로는 전지를 생각하면 된다.
• 전류의 정의에 의해 흡수전력 = - 공급전력 으로 표현이 가능하다.

요약

• 전하: 전류의 총합, 단위는 C
  $q= \int_{0}^{t}i(\tau)d\tau$
• 전류: 전하의 흐름, 전하를 시간단위로 미분한 값 단위는 A
  $i = \frac{dq}{dt}$
• 전압: 두 소자간의 흐르는 에너지 단위는 w
  $p = v * i$
• 에너지 $p = \frac{dw}{dt}$이므로, 역으로 산출 단위는 J
  $w= \int_{0}^{t}p(\tau)d\tau$