키르히호프의 법칙

회로를 마디의 관점으로 봐서 전류와 전압을 쉽게 풀어내는 법칙이다.

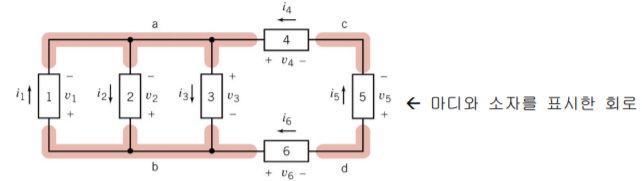
• 마디(Node)란 전압의 입장으로 본 하나의 덩어리. 전압계를 마디 어디에 두어도 마디의 전압은 같다. ex)위의 사진에서, $v_1$의 마디는 $v_2$의 양 단자의 끝 점 전까지가 모두 $v_1$의 단자이다.

키르히호프의 전류법칙 (Kichhoff's Current Law, KCL)

• 마디에 들어오는 모든 전류의 수학적 합은 언제나 0
  마디에 들어오는 전류의 방향을 통일하는 것이 중요하다!
  (ex) 마디에 들어오는 전류를 +라고 하면, 마디를 나가는 전류를 -라고 해야한다.)
  
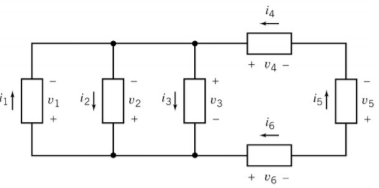
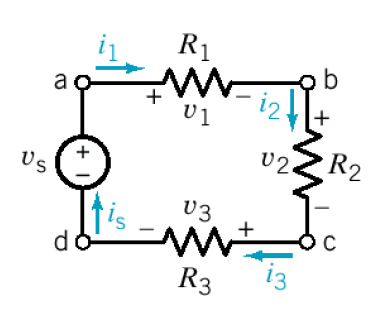
  다음과 같은 회로가 있을 때, C단자의 전류의 합은 4번에서 흘러들어온 전류 + 5번에서 흘러들어오는 전류 = 0이 되어야 한다.

키르히호프의 전압법칙 (Kirchhoff's Voltage Law, KVL)

루프 주변 전압의 수학적 합은 언제나 0, 이때, 부호를 조심해야한다. KVl에서는 통상 시계방향으로 회전하면서, 만나는 부호를 그 전압의 부호로 설정한다.
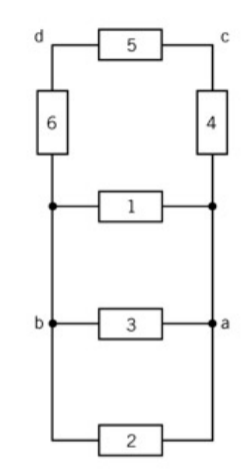
(루프라고 하면, 여러 마디로 둘러싸인 한 부분을 말한다. 자세한건 다음 사진 참조)

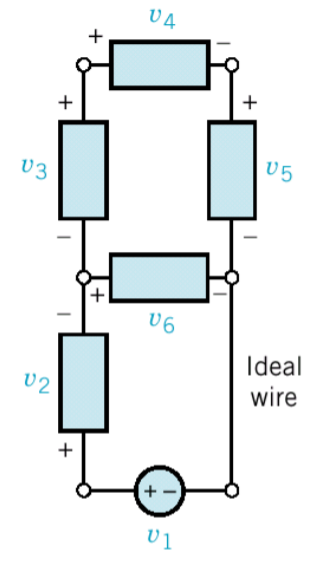
다음과 같은 회로가 존재할 때, $v_3, v_4, v_5,v_6$은 같은 루프에 존재한다. 즉, KVL법칙에 따라 , $v_4+v_5-v_6-v_3=0$을 만족한다.

직렬저항과 전압분배(Series Resistors and Voltage Division)

• 회로가 직렬로 되어있을 경우 각 마디에 KCL을 적용하면,
  a: $i_1 = i_s$, b: $i_1 = i_2$, c: $i_2 = i_3$, d: $i_3 = i_s$
  $i_1 = i_2 = i_3 = i_s$이 성립한다. 즉, 직렬연결이면 모든 소자에 흐르는 전류가 동일하다.
• 위의 회로에 KVL을 적용하면, $v_1 + v_2+ v_3- v_s = 0 (1)$ (1)식에 Ohm의 법칙($v = R\cdot i$)을 적용해서 다시 쓰면, $i_1\sdot R_1+ i_2\sdot R_2 + i_3\sdot R_3=v_s$이다. 따라서 $i_1 = \frac{v_s}{R_1+R_2+R_3}$이 성립한다.
  n번째의 저항을 $R_N$이라고 할때, 전압 $v_n = i_1\sdot R_n =\frac{v_s\sdot R_n}{R_1+R_2+R_3}$가 된다.
  이때 $R_1+ R_2 = R_3= R_s$ 즉 $R_s$는 모든 저항의 합의로 정의한다.
• 정리하면, 루프가 직렬저항일때 전류$i_s$는 같고, n번째 저항$R_n$의 전압은 $v_n = v_s\sdot \frac{R_n}{R_s}$이다.

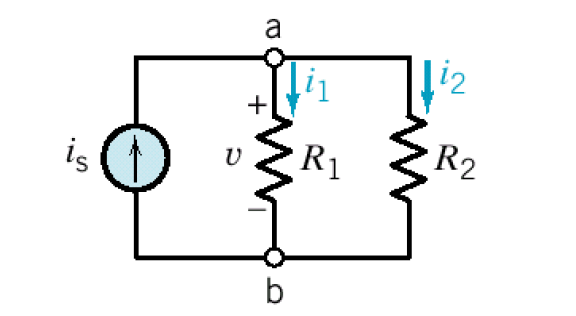
병렬저항과 전류분배(Parallel Resistors and Current Division)

• 마디 a에 KCL을 적용하면, $i_s = i_1+i_2$가 성립. Ohm의 법칙을 써서 다시 정리하면, $i_s = \frac{v}{R_1}+ \frac{v}{R_2}$(병렬연결이므로, $R_1$과 $R_2$의 전압은 같다). 이를 Conductance ($G = \frac{1}{R}$)로 표현해보면,, $i_s =v\sdot(G_1+ G_2)$ $G_p = G_1+G_2$라고 하면 다음과 같은 식이 성립한다. $G_p = \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2}$ , $R_p$에대해서 다시 풀어보면, $R_p= \frac{R_1 \sdot R_2}{R_1+ R_2}$이 된다.(주의해야할 것이 $R_p$의 공식은 저항이 구하려는 저항2개가 병렬저항일 때만 사용이 가능하다. $R_1, R_2$ 외에도$R_3$가 존재한다면, 위의 $R_p$의 식은 성립하지 않음)

---

• 전류분배 : 위의 식에서 $i_1= G_1\cdot v$이다.이를 일반화 하면, $i_s=\sum_{n=1}^N G_n \cdot v$이기때문에, $v =\frac{i_s}{\sum_{n=1}^N G_n}$이 성립한다. 이때, 병렬저항에서 n번째 노드의 전류 $i_n = v_n \cdot G_n = G_n \cdot \frac{i_s}{\sum_{n=1}^N G_n} = i_S\sdot \frac{G_n}{G_p}$라는 일반식이 성립한다.